Важнейшие научные результаты Института математики за 2021 год

1. Описаны определимые (без параметров и с параметрами) подгруппы делимой жёсткой группы.

Более десяти лет назад Н. С. Романовский дал определение жёсткой (разрешимой) группы и в последующих его и, совместных с А. Г. Мясниковым, работах была развита алгебраическая геометрия над жёсткими группами, сформулирована и доказана теорема Гильберта о нулях. Оказалось также, что класс жёстких групп исключительно интересен с точки зрения теории моделей, а теория делимых m-жёстких групп во многом похожа на классическую теорию алгебраически замкнутых полей. Для неё найдена рекурсивная система аксиом, доказаны полнота и омега-стабильность, описаны насыщенные модели, получена элиминация кванторов до булевой комбинации АЕ-формул. В этом направлении находится описание определимых подгрупп делимой жёсткой группы.
ТЕОРЕМА 1. Члены жёсткого ряда делимой жёсткой группы и только они являются определимыми в сигнатуре теории групп без параметров подгруппами.
ТЕОРЕМА 2. Подгруппа делимой жёсткой группы является определимой в сигнатуре теории групп с параметрами тогда и только тогда, когда она представляется в виде подпроизведения некоторого расщепления данной группы в полупрямое произведение абелевых подгрупп.

[1] Н. С. Романовский. Делимые жёсткие группы. IV. Определимые подгруппы // Алгебра и логика, 59:3 (2020), 344-366
[2] Groups and Model Theory. GAGTA Book 2. De Gruyter, 2021 (chapter 5: Nikolay Romanovskii, Rigid solvable groups. Algebraic geometry and model theory, 193-229).

2. По определению, группа G насыщена данным множеством M групп, если любая конечная подгруппа из G содержится в подгруппе, изоморфной некоторому элементу множества M. Доказано, что периодическая группа, насыщенная множеством конечных простых ортогональных групп фиксированной нечётной размерности n, изоморфна ортогональной группе размерности n над подходящим локально конечным полем. В частности, она локально конечна и счётна.

По определению, группа G насыщена группами из данного множества M групп, если каждая конечная подгруппа группы G содержится в подгруппе, изоморфной некоторому элементу множества M. Известно, что локально конечная группа, насыщенная множеством конечных простых групп лиева типа ограниченного лиева ранга, изоморфна простой группе лиева типа над локально конечным полем (независимо показано в работах Беляева, Боровика, Хартли и Шюта, Томаса (1984-85)). Из этого результата, в частности, вытекает классификация простых периодических групп матриц.

Остаётся ли справедливым отмеченный результат, если заменить условие локальной конечности группы на условие её периодичности? Ответ на этот чрезвычайно сложный вопрос до последнего времени был известен только в случаях, когда M состоит из групп лиева ранга 1 или 2. Авторам удалось положительно решить его для групп лиева типа B_n=O_2n+1 при произвольном натуральном ранге n.

[1] Д. В. Лыткина, В. Д. Мазуров. Локальная конечность периодических групп, насыщенных конечными простыми ортогональными группами нечётной размерности // Сибирск. матем. журн., 62:3 (2021), 572-578.

3. Доказано, что произвольный оператор Роты-Бакстера веса 0 на унитальной конечномерной алгебре нильпотентен.

Оператор Роты — Бакстера веса 0 является алгебраическим аналогом интегрального оператора. Доказано, что произвольный оператор Роты — Бакстера веса 0 на унитальной ассоциативной (альтернативной или йордановой) алгебраической алгебре над полем характеристики 0 нильпотентен. В частности, этот результат верен и для конечномерных алгебр. Для данной алгебры A определяется новый инвариант rb(A) — индекс нильпотентности операторов Роты — Бакстера веса 0 на алгебре A. Установлено, что rb(M_n(F)) = 2n-1 над полем F характеристики 0.

[1] V. Gubarev. Rota-Baxter operators on unital algebras // Moscow Mathematical Journal, 21:2 (2021), 325-364.

4. Описаны 3-порожденные аксиальные алгебры йорданова типа.

Аксиальные алгебры йорданова типа η - это коммутативные алгебры, порожденные идемпотентами, с некоторыми дополнительными свойствами. Эти свойства обобщают разложения Пирса для йордановых алгебр, где 1/2 заменяется на η. В частности, йордановы алгебры, порожденные идемпотентами, являются аксиальными алгебрами йорданова типа 1/2. Если η не равно 1/2, то известно, что аксиальные алгебры йорданова типа η являются факторами так называемых алгебр Мацуо, соответствующих группам 3-транспозиций. Известно, что алгебра йорданова типа, порожденная двумя примитивными осями, имеет размерность не более трех.
В нашей работе доказано, что каждая аксиальная алгебра йорданова типа, порожденная тремя примитивными осями, имеет размерность не более девяти. Также была построена универсальная 3-порожденная аксиальная алгебра йорданова типа η.

[1] Gorshkov, Ilya; Staroletov, Alexey. On primitive 3-generated axial algebras of Jordan type // J. Algebra, 563 (2020), 74–99.

5. Доказано существование вложения произвольной конечно порождённой разрешимой группы ступени разрешимости l в 4-порождённую разрешимую группу ступени разрешимости l+1.

В 1959 году Б. и Х. Нейман установили с помощью конструкции сплетения, что любая счётная группа G из многообразия M вложима в 2-порождённую группу H из многообразия MA^2, где A – многообразие абелевых групп. Из доказательства следует, что любая счётная разрешимая группа G ступени разрешимости d вложима в 2-порождённую разрешимую группу ступени d+2. Оценку d+2 в общем случае улучшить нельзя, но для конечно порождённых разрешимых групп вопрос о снижении оценки до d+1 остался открытым. В. Г. Микаелян и А. Ю. Ольшанский поставили вопрос о возможности вложения в группу H с числом порождающих зависящем только от d.
Основные результаты автора опубликованы в [1] (краткое изложение в [2]). Установлено, что любая счётная группа G из произвольного многообразия M, у которой фактор группа по коммутанту G/G’ – прямое произведение свободной абелевой группы и конечной группы, вложима в 4-порождённую группу H из многообразия MA. Отсюда следует приведенный выше важнейший результат, естественное дополнение теоремы Нейманов и решение проблемы Микаеляна-Ольшанского. Более того, если G/G’ - свободная абелева, то группу H можно выбрать 2-порождённой. На группу H переносятся свойства конечности и периодичности группы G.

[1] V. A. Roman’kov. Embedding theorems for solvable groups // Proc. Amer. Math. Soc., 149 (2021), 4133-4143. DOI: https://doi.org/10.1090/proc/15562
[2] В. А. Романьков. Две проблемы о разрешимых и нильпотентных группах // Алгебра и логика, 59:6 (2020), 719–733. DOI: https://doi.org/10.33048/alglog.2020.59.606

6. Найдено изоморфное представление для структуры функций, вычислимых на машинах Блюм-Шуба-Смейла, работающих в бесконечном времени, при помощи функций, задаваемых специфическими инфинитарными формулами.

Вычислимость на машинах Блюм-Шуба-Смейла, работающих в бесконечном времени (ITBM-вычислимость), отличается от обычной вычислимости на этих машинах возможностью производить бесконечные вычисления во времени, задаваемом ординалами. Существуют аргументы в пользу того, что данная вычислимость достаточна для характеризации функций и множеств, определимых в анализе.

Найдено изоморфное представление для структуры ITBM-вычислимых функций при помощи функций, задаваемых специфическими инфинитарными (так называемыми малыми) формулами. Кроме того, получен ряд результатов, демонстрирующих отличие ITBM-вычислимости от классический, охарактеризованы все возможные области значений и области определений ITBM-вычислимых функций, изучена выполнимость аналога теоремы Кантора-Бернштейна для ITBM-вычислимых функций.

[1] П. Кёпке, А. С. Морозов. Характеризации ITBM-вычислимости. II // Алгебра и логика, 60:1 (2021), 39-56.
[2] П. Кёпке, А. С. Морозов. Характеризации ITBM-вычислимости. I // Алгебра и логика, 59:6 (2020), 627-648.

7. Показано, что непрерывность плотного линейного порядка является необходимым и достаточным условием равенства степеней сложности порядка и его интервального расширения. Найдены приложения полученных результатов при описании алгоритмических свойств интервальной семантики глаголов в естественных языках.

Исследуются алгоритмические свойства интервальных расширений плотных линейных порядков, в частности, степени сложности (а именно, sΣ-степени) таких расширений. Показано, что непрерывность является необходимым и достаточным условием равенства степеней сложности порядка и его интервального расширения. Этот критерий позволяет получить серию положительных результатов, относящихся к проблеме описания несчетных структур, Σ-определимых над плотными линейными порядками. Возникающие при этом темпоральные аппроксимационные пространства над интервальными расширениями рассматриваются как математические модели семантики глаголов в естественных языках, обобщающие модели Р. Монтегю и Б. Пати. Показано, что непрерывность порядка влечет эффективность проверки истинности $Δ_0^{DL}$ -формул в темпоральных пространствах над sc-простыми обогащениями. Как следствие, получено эффективное описание интервалов, соответствующих различным временам глаголов, что можно считать примером использования обобщенной вычислимости в математической лингвистике.

[1] Alexey Stukachev. Approximation spaces of temporal processes and effectiveness of interval semantics, Advances in Intelligent Systems and Computing, 1242 (2021), 53-61.
[2] Стукачев А. И. Интервальные расширения порядков и темпоральные аппроксимационные пространства // Сибирский математический журнал, 62:4 (2021), 894-910.

8. Для многих известных квазимногообразий алгебраических систем, среди которых квазимногообразия абелевых групп с константой, коммутативных колец, графов, канторовых алгебр, унаров, дифференциальных группоидов и многие другие, установлено существование континуума нестандартных подквазимногообразий.

Согласно классическому определению, предмногообразие К называется стандартным, если любая булева топологическая система из К является проконечной в К. Ранее авторами были найдены условия, при выполнении которых квазимногообразие алгебраических систем устроено весьма сложно с различных точек зрения. Оказывается, что при выполнении этих условий квазимногообразие К является сложным и в топологическом смысле. А именно, в этом случае К содержит континуум нестандартных квазимногообразий, имеющих конечно разбиваемый базис квазитождеств, и континуум нестандартных квазимногообразий без такого базиса. Этот результат применим к весьма широкому спектру конкретных квазимногообразий алгебраических систем.

[1] А. В. Кравченко, А. М. Нуракунов, М. В. Швидефски. О сложности решёток квазимногообразий IV. Нестандартные квазимногообразия // Сибирский математический журнал, 62:5 (2021), 1049-1060.

9. Получен критерий предельной распознаваемости для семейств вычислимых алгебраических структур с точностью до изоморфизма.

В алгоритмической теории обучения (algorithmic learning theory) изучаются алгоритмы распознавания различных математических объектов (в частности, формальных языков). В рамках алгоритмической теории обучения изучен вопрос о предельной распознаваемости семейств вычислимых алгебраических структур. Получено полное теоретико-модельное описание таких семейств, являющихся предельно распознаваемыми с точностью до изоморфизма: семейство распознаваемо в том и только том случае, когда соответствующие типы изоморфизма можно отделить друг от друга с помощью бесконечных $\Sigma_2$-предложений. Полученное теоретико-модельное описание имеет и вычислимый аналог. Установлено, что не существует предельно распознаваемого, бесконечного семейства линейных порядков.

[1] Bazhenov N., Fokina E., San Mauro L. Learning families of algebraic structures from informant // Information and Computation, 275 (2020), article id 104590.

10. Изучены решеточные свойства структуры степеней вычислимых метрик на польском пространстве по вычислимой сводимости, а также вопрос о существовании максимальных элементов в этой структуре. Показано, что упорядочение подмножеств счетного множества изоморфно вкладывается в структуру степеней метрик на вещественных числах по слабой сводимости над стандартной метрикой.

Общий подход к теории вычислимости на несчетных структурах с помощью представлений через последовательности натуральных чисел был разработан Крайцем и Вайраухом в 80-х годах. Вычислимая сводимость метрик на польском пространстве индуцируется сводимостью соответствующих представлений Коши; интуитивно, одна метрика сводится к другой, если тождественная функция вычислима относительно этих метрик. Можно ввести понятие слабой сводимости метрик, означающее вычислимость какого-нибудь автогомеоморфизма данного пространства относительно этих метрик.

Изучаются некоторые элементарные свойства структур степеней по этим сводимостям. Упорядочение степеней вычислимых метрик на произвольном польском пространстве по вычислимой сводимости образует нижнюю полурешетку. При выполнении достаточно естественных условий эта структура не содержит минимальных элементов, а также не является верхней полурешеткой. Если пространство некомпактно, эта полурешетка не содержит максимальных элементов. Также показано, что упорядочение подмножеств множества натуральных чисел по включению изоморфно вкладывается в упорядочение степеней метрик на вещественных числах по слабой сводимости над степенью стандартной метрики.

[1] R. Kornev. Computable metrics above the standard real metric // Sib. Electron. Math. Rep., 18:1 (2021), 377–392.
[2] Р. А. Корнев. Полурешетка степеней вычислимых метрик // Сиб. мат. журнал, 62:5 (2021), 1013–1038.

11. Доказано, что нетривиальность характеристического класса Годбийона-Вея-Лосика слоения Риба зависит от скорости сходимости некомпактных листов к компактному. Показана нетривиальность характеристического класса Черна-Лосика слоения Риба.

Классы Годбийона-Вея-Лосика и Черна-Лосика являются обобщением соответствующих классических характеристических классов слоений коразмерности один. Они принимают значения в расслоении реперов второго порядка над пространством листов слоения. Интерес к этим классам обусловлен тем, что они могут быть нетривиальны при тривиальности их классических аналогов, и потому могут нести дополнительную информацию о топологии слоений. В частности, классы Годбийона-Вея и Черна слоения Риба тривиальны. В работе рассмотрен класс слоений Риба, зависящих от вещественного параметра, определяющего скорость сходимости некомпактных листов к компактному. Доказано, что тривиальность класса Годбийона-Вея-Лосика равносильна тому, что вещественный параметр является четным целым числом. Кроме того, показано, что класс Черна-Лосика всегда нетривиален.

[1] Ya.V. Bazaikin, A.S. Galaev & P. Gumenyuk. Non-diffeomorphic Reeb foliations and modified Godbillon-Vey class
// Mathematische Zeitschrift (2021) Published: 06 August 2021. doi: 10.1007/s00209-021-02828-1, https://link.springer.com/article/10.1007%2Fs00209-021-02828-1
[2] Ya. V. Bazaikin and A.S. Galaev. Losik classes for codimension-one foliations // Journal of the Institute of Mathematics of Jussieu (2021). Published online by Cambridge University Press: 08 January 2021. Doi: 10.1017/S1474748020000596.
https://www.cambridge.org/core/journals/journal-of-the-institute-of-mathematics-of-jussieu/article/abs/losik-classes-for-codimensionone-foliations/5013B99C49A88A7CC38EBFF67D7ABE1E

12. Найдены анормальные экстремали левоинвариантных субфинслеровых квазиметрик на связных четырехмерных группах Ли, определяемых полунормами на левоинвариантных двумерных вполне неголономных распределениях, и критерии (не)строгой анормальности этих экстремалей.

Полунорма F на 2-МЕРНОМ подпространстве p алгебры Ли G_e ПРОИЗВОЛЬНОЙ связной 4-МЕРНОЙ группы Ли G задает левоинвариантную субфинслерову квазиметрику d на G, если 1)p порождает G_e (G_e - наименьшая алгебра Ли, включающая p);
2) F(u)=0 для u из p только для u=0. Экстремаль в (G,d) --- параметризованный длиной дуги путь g(t), заданный на некотором максимальном интервале I и удовлетворяющий принципу максимума Понтрягина (ПМП) левоинвариантной задачи оптимального быстродействия с областью управления U – единичным замкнутым шаром полунормы F. Экстремаль называется анормальной, если максимум из ПМП может быть нулем; строго (нестрого) анормальной, если он всегда 0 (может быть и >0). Доказано, что 1) анормальная экстремаль на (G,d) всегда существует и с точностью до перепараметризации есть единственная 1-параметрическая подгруппа или ее левый сдвиг; 2) в терминах структуры алгебры Ли G_e и двойственной для F полунормы F_U найдены ОБЩИЕ критерии (не)строгой анормальности экстремали;
3) определены алгебры Ли G_e, имеющие порождающее подпространство р; 4) для каждой такой алгебры Ли G_e найдено точное число порождающих ее подпространств p (они отождествляются, если переводятся друг в друга автоморфизмом алгебры G_e). Ранее были известны лишь весьма частные условия (не)строгой анормальности экстремали.

[1] Берестовский В. Н., Зубарева И. А. Анормальные экстремали левоинвариантных субфинслеровых квазиметрик на четырехмерных группах Ли // Сибирский математический журнал, 62:3 (2021), 481-501.

13. Доказаны оптимальные оценки соединимости горизонтальными ломаными в серии групп Карно.

Пусть G - группа Карно топологической размерности N=top dim G и глубины r. Из классической теоремы Рашевского - Чоу следует, что найдется число κ(G) такое, что любые две точки группы G можно соединить горизонтальной ломаной, состоящей не более чем из κ=κ(G) звеньев, где каждое звено – отрезок единичной длины интегральной линии некоторого векторного поля, являющегося линейной комбинацией базисных левоинвариантных векторных полей группы G (горизонтальная κ-ломаная). Хорошо известны оценки на величину κ(G) : κ(G) ≤ N(3·2^r-1 -2) (A. Bonfiglioli - E. Lanconelli - F. Uguzzoni), κ(G) ≤2N (Agrachev A.- Barilari D.-Boscain U.) Для ряда групп Карно получены точные значения величины κ(G).

Теорема 1 [1, 2]. 1) Пусть E - группа Энгеля, тогда κ(E) =4=top dim E,
2) пусть K-группа Картана, тогда κ(K) =5=top dim K,
3) пусть D- произвольная 2-ступенчатая группа Карно с горизонтальным распределением коранга 1, тогда κ(D)=3.

[1] Greshnov, A. V. Optimal horizontal joinability on the Engel group // Rend. Lincei Mat. Appl., 32 (2021), 535–547.
[2] Грешнов А. В., Жуков Р. И. Горизонтальная соединимость на канонической 3-ступенчатой группе Карно с горизонтальным распределением коранга 2 // Сиб. мат. журнал, 62:4 (2021), 736–746.

14. Построено богатое семейство римановых метрик на двумерных поверхностях, геодезический поток которых обладает дополнительным рациональным по импульсам первым интегралом с линейными числителем и знаменателем.

Интегрирование геодезических потоков на поверхностях является важным направлением современной математики и механики, которое имеет длительную историю. Несмотря на интенсивные исследования в этой области более или менее хорошо изучены и классифицированы на данный момент лишь полиномиальные по импульсам интегралы невысоких степеней. С другой стороны, неполиномиальные (скажем, рациональные) интегралы подобных систем исследованы в заметно меньшей степени, и примеров таких интегралов на данный момент известно крайне мало.
Исследованы интегрируемые геодезические потоки на двумерных поверхностях, обладающие дополнительным рациональным по импульсам первым интегралом. В простейшем случае, когда степени числителя и знаменателя интеграла равны единице, удалось построить богатый запас явных примеров римановых метрик и соответствующих первых интегралов. В некоторых из построенных примеров имеются также квадратичные интегралы, то есть эти системы являются суперинтегрируемыми.

[1] S. Agapov, V. Shubin. Rational integrals of 2-dimensional geodesic flows: new examples // Journal of Geometry and Physics, 170 (2021), 104389. https://doi.org/10.1016/j.geomphys.2021.104389

15. Разработана обобщающая концепция геометрической теории функции, содержащая в качестве частного случая все известные подходы к задачам квазиконформного анализа.

Определена двухиндексная шкала $\mathcal{Q}_{q,p}$, n-1 < q ≤ p < ∞ (1 ≤ q ≤ p < ∞ при n=2), гомеоморфизмов пространственных областей в Rⁿ, геометрическое описание которых обусловленно контролем поведения q-емкости конденсаторов в образе через весовую p-емкость конденсаторов в прообразе. При q = p = n класс отображений $\mathcal{Q}_{n,n}$ содержит совокупность, так называемых, $\mathcal{Q}$-гомеоморфизмов, активно исследуемых в течение последних 25 лет. Получено эквивалентное функциональное и аналитическое описание классов $\mathcal{Q}_{q,p}$ , основанное на свойствах оператора композиции весового пространства Соболева в невесовое, индуцированного отображениями, обратными к отображениям класса $\mathcal{Q}_{q,p}$ . Доказана также эквивалентность определений $\mathcal{Q}_{q,p}$ -гомеоморфизмов на модульном и емкостном языках.

[1] Водопьянов С. К. ОцеОператоры композиции в весовых пространствах Соболева и теория $\mathcal{Q}_{q}$ -гомеоморфизмов // Докл. АН. Математика, информатика, процессы управления, 494:5 (2020), 21-25.
[2] Водопьянов С. К. Об аналитических и геометрических свойствах отображений в теории $\mathcal{Q}_{q,p}$ -гомеоморфизмов
// Математические заметки, 108:6 (2020), 924--928.
[3] Водопьянов С. К. О регулярности отображений, обратных к соболевским, и теория $\mathcal{Q}_{q,p}$ -гомеоморфизмов // Сиб. мат. журн., 61:6 (2020), 1257-1299.
[4] Водопьянов С. К. Об эквивалентности двух подходов к задачам квазиконформного анализа // Сиб. мат. журн., 62:6 (2021), 1010-1025.

16. Доказаны существование и единственность булевозначной системы, удовлетворяющей аксиомам Соловея — Тенненбаума, и установлена логическая независимость этих аксиом.

Аксиоматическое описание булевозначного универсума, предложенное Робертом Соловеем и Стэнли Тенненбаумом в 1971 году, до сих пор оставалось без обоснования. В представляемой серии статей впервые приведено соответствующее обоснование, причем с математически строгой детализацией всех сопутствующих формальных процедур, ранее не встречавшейся в литературе. Мы не только устанавливаем существование и единственность булевозначной системы, удовлетворяющей аксиомам Соловея — Тенненбаума, но и показываем, что эти аксиомы логически независимы. Этой цели удалось достичь благодаря введению и исследованию нового понятия универсума над произвольной экстенсиональной булевозначной системой.

[1] Гутман А. Е. Булевозначный универсум как алгебраическая система. I. Основные принципы // Сиб. матем. журн., 60:5 (2019), 1041–1062. DOI: 10.33048/smzh.2019.60.505 Gutman A.E. Boolean-valued universe as an algebraic system. I: Basic principles // Sib. Math. J., 60:5 (2019), 810–827. DOI: 10.1134/S0037446619050057
[2] Гутман А. Е. Булевозначный универсум как алгебраическая система. II. Интенсиональные иерархии // Сиб. матем. журн., 61:3 (2020), 539–571. DOI: 10.33048/smzh.2020.61.305 Gutman A.E. Boolean-valued universe as an algebraic system. II: Intensional hierarchies // Sib. Math. J., 61:3 (20202), 426–452. DOI: 10.1134/S0037446620030052
[3] Gutman A. E. Boolean-valued set-theoretic systems: General formalism and basic technique // Mathematics, 9:9 (2021), Art. 1056. 78 pages. DOI: 10.3390/math9091056

17. Доказано существование оценок скорости поточечной сходимости в эргодической теореме Биркгофа, справедливых п.в.

Доказано, что монотонные оценки скорости поточечной сходимости в эргодической теореме Биркгофа (для эргодических динамических систем как с дискретным, так и с непрерывным временем) имеют место на множестве либо полной меры, либо нулевой. Показано, что такие оценки, справедливые п.в., всегда существуют. Получены критерии максимально возможной рассматриваемой скорости сходимости; доказано, что больших скоростей не бывает.

[1] Качуровский А. Г., Подвигин И. В., Свищёв А. А. Максимальная поточечная скорость сходимости в эргодической теореме Биркгофа // Записки научных семинаров ПОМИ, 498 (2020), 18–25.
[2] Podvigin I. V. Lower bound of the supremum of ergodic averages for Z^d and R^d-actions // Сиб. электрон. мат. изв., 17 (2020), 626–636.
[3] Качуровский А. Г., Подвигин И. В. Об измерении скоростей сходимости в эргодической теореме Биркгофа // Матем. заметки, 106:1 (2019), 40–52.

18. Установлены условия экспоненциальной устойчивости решений неавтономных систем дифференциальных уравнений с распределенным запаздыванием и получены оценки норм решений.

Рассмотрены некоторые классы систем дифференциальных уравнений с распределенным запаздыванием и периодическими коэффициентами в линейных членах. С использованием специальных функционалов Ляпунова – Красовского установлены достаточные условия экспоненциальной устойчивости, получены оценки норм решений систем на полупрямой {t>0}, характеризующие скорость убывания на бесконечности, указаны оценки на множества притяжения. Условия устойчивости формулируются в терминах матричных и интегральных неравенств. Установлены оценки на возмущения матричных коэффициентов в линейной части, при которых сохраняется экспоненциальная устойчивость. Полученные результаты вошли в диссертацию на соискание ученой степени кандидата физико-математических наук по специальности 01.01.02, которая была защищена 29 июня 2021 года.

[1] Т. Ыскак. Оценки решений одного класса систем уравнений нейтрального типа с распределенным запаздыванием
// Сибирские электронные математические известия, 17 (2020), 416–427.
[2] Т. Ыскак. Оценки решений одного класса систем нелинейных дифференциальных уравнений с распределенным запаздыванием // Сибирские электронные математические известия, 17 (2020), 2204–2215.
[3] Т. Ыскак. Об оценках решений систем нелинейных дифференциальных уравнений с распределённым запаздыванием и периодическими коэффициентами в линейной части // Сиб. журн. индустр. матем, 24:2 (2021), 148–159.

19. Предложен Метод коллокаций для расчёта устанавливающихся течений полимерной жидкости типа Пуазейля.

Предложен метод численного решения нелинейных краевых и начально-краевых задач для уравнений второго порядка. Метод основан на применении модифицированных интерполяционных полиномов с узлами в нулях полинома Чебышёва и на аппроксимации дифференциальных уравнений задачи с помощью матричных уравнений Сильвестра и их тензорных обобщений. На каждой итерации по времени метод имеет вычислительную сложность O(N1+1/d), где N=N1×…×Nd – число узлов пространственной сетки, d – размерность задачи, N_i – число узлов по i-й координате. В вычислительных экспериментах показано увеличение порядка сходимости метода при увеличении порядка гладкости искомой функции в соответствии с оценками погрешности наилучших полиномиальных приближений, что является косвенным подтверждением отсутствия насыщения. С применением интервального анализа проведено исследование спектра и чисел обусловленности матриц, используемых в методе. При решении модельной линейной задачи для уравнения Пуассона доказаны теоремы об аппроксимации и устойчивости метода с использование критерия фон Неймана.

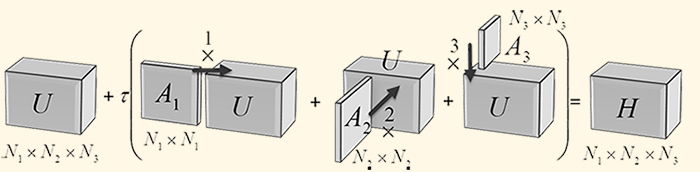
Рис. 1. Схема метода для трёхмерной задачи. Матрицы A₁, A₂, A₃ аппроксимируют операторы дифференцирования по координатам 1,2,3, тензоры U и H содержат значения решения и правой части в узлах коллокации, $\tau$ – шаг сетки по времени, “×” с верхним индексом – операция свёртки

[1] Блохин А. М., Семисалов Б. В. Расчёт стационарных неизотермических МГД течений полимерной жидкости в каналах с внутренними нагревательными элементами // Сиб. журн. индустр. матем., 23:2 (2020), 17–40.

20. Доказаны теоремы о существовании и устойчивости периодических решений класса систем нелинейных дифференциальных уравнений, линейная часть которых экспоненциально дихотомична и имеет периодические коэффициенты.

Изучена задача о периодических решениях класса систем нелинейных дифференциальных уравнений, линейная часть которых экспоненциально дихотомична и имеет периодические коэффициенты. На основе критерия экспоненциальной дихотомии, установленного в работах Г. В. Демиденко (2016), доказаны теоремы о возмущении для экспоненциальной дихотомии для линейных дифференциальных уравнений с периодическими коэффициентами, о существовании периодических решений рассматриваемого класса систем нелинейных дифференциальных уравнений, об устойчивости периодических решений относительно малых возмущений коэффициентов в линейной части и нелинейных членов [1]. В качестве приложения рассмотрена задача об устойчивости движения перевернутого маятника, точка подвеса которого совершает высокочастотные колебания вдоль прямой, составляющий малый угол с вертикалью. Доказано, что при выполнении некоторых условий на функцию, описывающую колебания точки подвеса, возникает периодическое движение маятника и оно является асимптотически устойчивым [2]. В случае высокочастотных гармонических колебаний точки подвеса вдоль вертикали эти условия совпадают с условиями Н. Н. Боголюбова.

[1] Демиденко Г. В. Об одном классе систем дифференциальных уравнений с периодическими коэффициентами в линейных членах // Сибирский математический журнал, 62:5 (2021), 995-1012.
[2] Демиденко Г. В., Дулепова А. В. О периодических решениях одного дифференциального уравнения второго порядка // Современная математика. Фундаментальные направления, 67:3 (2021), 535–548.

21. Доказана устойчивость и единственность обнаруженных ранее циклов в инвариантных областях фазовых портретов динамических систем кинетического типа.

В фазовых портретах кусочно-линейных динамических систем размерностей 4, 5 и 6, моделирующих кольцевые генные сети, построены инвариантные области, содержащие по одному циклу. Доказана устойчивость таких циклов. Вне этих инвариантных областей рассматриваемые динамические системы размерностей 5 и выше могут иметь и другие циклы. Для подобной гладкой системы размерности 6 описана двумерная инвариантная поверхность, содержащая соответствующий цикл. Доказано, что трёхмерные динамические системы, моделирующие циркадные осцилляторы, циклов не имеют. Для моделей размерности 6 и 7 получены условия существования циклов у циркадных осцилляторов. Все результаты новые, опубликованы в 2021 и в конце 2020.


Проекция траектории и её предельного цикла шестимерной модели циркадного осциллятора на двумерную плоскость, соответствующую собственным числам матрицы линеаризации с положительными вещественными частями.(иллюстрация
А. А. Акиньшина)

[1] Likhoshvai V. A., Golubyatnikov V. P., Khlebodarova T .M. Limit cycles in models of circular gene networks regulated by negative feedbacks // BMC Bioinformatics, 21:11 (2020), 255, 15 pages. DOI:10.1186/s12859-020-03598-z
[2] Golubyatnikov V. P., Minushkina L. S. Combinatorics and geometry of circular gene networks models // Письма в Вавиловский журнал генетиков и селекционеров, 6:4 (2020), 188-192. DOI 10.18699/Letters2020-6-24
[3] Кириллова Н. Е. Об инвариантных поверхностях в моделях генных сетей // СЖИМ, 23:4 (2020), 69-76.
DOI 10.33048/SIBJIM.2020.23.405
[4] Golubyatnikov V. P., Minushkina L. S. On uniqueness and stability of a cycle in one gene network // SEMR, 18:1 (2021), 464-473. DOI 10.33048/semi.2021.18.032
[5] Golubyatnikov V. P., Minushkina L. S. On geometric structure of phase portraits of some piecewise linear dynamical systems // Tbilisi Mathematical Journal, 7 (2021), 49-56.
[6] Минушкина Л. С. Фазовые портреты блочно-линейной динамической системы в одной модели кольцевой генной сети
// Матем. Заметки СВФУ, 28:2 (2021), 34-46. DOI: 10.25587/SVFU.2021.60.20.003
[7] Аюпова Н. Б., Голубятников В. П. Об одном цикле в пятимерной модели кольцевой генной сети // СЖИМ, 24:3 (2021), 19 -29. DOI 10.33048/SIBJIM.2021.24.302
[8] Голубятников В. П., Кириллова Н. Е. Фазовые портреты моделей двух генных сетей // Матем. Заметки СВФУ, 28:1 (2021), 3-11. DOI: 10 . 25587/SVFU.2021.68.70.001
[9] Голубятников В. П., Аюпова Н. Б., Кириллова Н. Е., Подколодная О. А., Подколодный Н. Л., Юношева Е. В. Об условиях существования циклов в двух базовых моделях циркадного осциллятора млекопитающих // СЖИМ, 24:4 (2021), 39-53.
DOI 10.33048/SIBJIM.2021.24.403

22. Для многомерного арифметического полумарковского обобщенного процесса восстановления получены локальные теоремы в областях нормальных, умеренно больших и частично больших уклонений.

Предметом исследования является многомерный арифметический полумарковский обобщенный процесс восстановления. В отличие от обычного обобщенного процесса восстановления этот тип процессов строится по случайному блужданию, в котором распределения суммируемых случайных величин зависят от состояний некоторой цепи Маркова.
Обобщенные процессы восстановления находят многочисленные применения в реальных задачах страхования, финансов, теории надежности, организации очередей. Так, например, в страховании обобщенные процессы восстановления описывают времена между наступлениями страховых случаев и суммы выплат по этим случаям. Более общим типом процессов являются полумарковские обобщенные процессы восстановления, они позволяют также учитывать случайные изменения среды, благодаря чему являются более точными моделями реальных процессов. Важной задачей является доказательство предельных теорем для этого типа процессов, такие теоремы находят применения также в прогнозировании и проверке статистических гипотез.

[1] A. Logachov, A. Mogulskii, Е. Prokopenko, A. Yambartsev. Local theorems for (multidimensional) additive functionals of semi-Markov chains // Stochastic Processes and their Applications, 137 (2021), 149-166. DOI: 10.1016/j.spa.2021.03.011

23. Предложен альтернативный метод доказательства эргодической теоремы для общих цепей Маркова.

В 1978 г. Атрейя и Ней и одновременно Нуммелин предложили для изучения эргодических свойств цепей Маркова с абстрактным множеством состояний так называемый метод расщепления. Суть этого метода состоит в том, что он позволяет выделить атом в расширенном фазовом пространстве. Это позволяет применить при доказательстве эргодических теорем традиционный для теории восстановления метод регенерации. Описанный подход позволил перечисленным выше авторам доказать эргодическую теорему лля цепей с конечной инвариантной мерой. В моей статье разработан аналитический метод, не требующий расщепления фазового пространства. Сначала выводится новое представление для инвариантной меры, а затем в терминах этой меры доказывается эргодическая теорема, включающая случай бесконечной инвариантной меры. В основе всех рассуждений лежит найденная мной формула для степени суммы двух элементов любого кольца.

[1] Нагаев С. В. Альтернативный метод доказательства эргодической теоремы для общих цепей Маркова // Теория вероятн. и ее примен., 66:3, 454–467; https://doi.org/10.4213/tvp5371

24. Предложены подходы к решению задач составления расписаний в системах с многопроцессорными работами и учетом расхода энергии. Это позволило разработать новые полиномиальные приближенные алгоритмы с гарантированными оценками точности.

Развитие современных компьютерных технологий позволяет не только решать сложные вычислительные задачи, но и порождает новые проблемы оптимального использования вычислительных ресурсов. Для выполнения трудоемких вычислений современные компьютеры могут как использовать несколько процессоров одновременно, так и динамически менять скорость вычислений за счет дополнительного расхода энергии. В цикле публикаций авторов впервые исследованы задачи теории расписаний с многопроцессорными работами как с критерием минимизации расхода энергии, так и с классическими критериями при бюджетных ограничениях на расход энергии.
Авторами предложен двухэтапный метод решения энергетических задач теории расписаний. Сначала вычисляется нижняя оценка целевой функции. Здесь также определяются скорости выполнения работ, которые позволяют достичь эту оценку при нарушении некоторых ограничений задачи. Это дает возможность на втором этапе перейти к решению задачи с фиксированными длительностями работ и найти допустимое расписание с гарантированно “хорошим” значением целевой функции.
Подходы к построению нижних оценок на целевую функцию, основаны: (1) на сведении релаксации исходной задачи к задаче о максимальном потоке минимальной стоимости специального вида; (2) на представлении исходной задачи как задачи выпуклого программирования и решении ее с использованием условий Каруша-Куна-Таккера; (3) на представлении исходной задачи как задачи линейного программирования с экспоненциальным числом переменных и полиномиальным числом ограничений и решении ее методом эллипсоидов с использованием полиномиального оракула отсечения. Исследованы свойства нижних оценок, получаемых на первом этапе. Это позволило разработать оригинальные приближенные алгоритмы полиномиальной трудоемкости с гарантированными оценками точности для различных практически значимых вариантов задачи.
При построении допустимых решений применяются либо жадные алгоритмы, либо методы декомпозиции. Доказано, что найденные относительные оценки точности алгоритмов являются неулучшаемыми на классах рассмотренных примеров (индивидуальных задач). Указанные результаты являются первыми приближенными алгоритмами с гарантированными оценками точности для многопроцессорных работ с учетом расхода энергии и обобщают известные результаты для однопроцессорных работ.

[1] Kononov A., Kovalenko Y. Approximate schedules for non-migratory parallel jobs in speed-scaled multiprocessor systems
// Siberian electronic mathematical reports, 16 (2019), 249–257. doi: 10.33048/semi.2019.16.016
[2] Kononov A., Kovalenko Y. Makespan minimization for parallel jobs with energy constraint // MOTOR-2020, LNCS, vol. 12095 (2020), 289–300. doi: 10.1007/978-3-030-49988-4_20
[3] Kononov A., Kovalenko Y. Approximation algorithms for energy-efficient scheduling of parallel jobs // Journal of Scheduling, 23:6 (2020), 693–709. doi: 10.1007/s10951-020-00653-8
[4] Kononov A., Kovalenko Y. Minimizing total completion time in multiprocessor job systems with energy constraint // MOTOR-2021, LNCS, vol. 12755 (2021), 267-279. doi: 10.1007/978-3-030-77876-7_18

25. Для интерполяции функций с большими градиентами в пограничном слое разработана неполиномиальная интерполяционная формула и проведен анализ погрешности кубического сплайна на сетке Бахвалова.

Вопрос интерполяции функций с большими градиентами в пограничном слое актуален, потому что применение многочлена Лагранжа и кубического сплайна приводит к существенным погрешностям, если возмущающий малый параметр соизмерим с шагом сетки. В случае равномерной сетки разработана интерполяционная формула с k узлами интерполяции (k>1), точная на сингулярной составляющей, известной с точностью до множителя и отвечающей за большие градиенты функции в пограничном слое. Доказана теорема, что если производные сингулярной составляющей порядка k и (k-1) внутри интервала интерполяции не обращаются в нуль, то интерполяционная формула имеет погрешность порядка (k-1) по шагу сетки, равномерно по сингулярной составляющей. Условия теоремы выполнены, например, в случаях экспоненциального и степенного пограничных слоев. Построенная интерполяционная формула обобщена на двумерный случай с сохранением оценки погрешности и применена для построения квадратурной формулы, точной на сингулярной составляющей. Для построенной составной квадратурной формулы получена оценка погрешности порядка (k-1) по шагу сетки, равномерно по сингулярной составляющей.
Оценена погрешность кубического сплайна на сетке Бахвалова при наличии экспоненциального пограничного слоя. Доказано, что кубический сплайн на сетке Бахвалова обладает четвертым порядком точности, равномерно по малому параметру. Получена оценка погрешности при вычислении производных функции с большими градиентами, заданной в узлах сетки Бахвалова, на основе построения и дифференцирования кубического сплайна .

[1] Задорин А. И., Задорин Н. А. Неполиномиальная интерполяция функций с большими градиентами и ее применение
// Журнал вычислительной математики и математической физики, 61:2 (2021), 179-188.
DOI: 10.31857/S0044466921020150.
[2] Блатов И. А., Задорин А. И., Китаева Е. В. Применение кубического сплайна на сетке Бахвалова при наличии пограничного слоя // Журнал вычислительной математики и математической физики, 61:12 (2021), 46-64.
DOI: 10.31857/S0044466921120073.
[3] Blatov I. A., Zadorin A. I. Application a cubic spline to calculate derivatives in the presence of a boundary layer // J. of Physics: Conf. Series, 1791 (2021), 012069. DOI:10.1088/1742-6596/1791/1/012069.

26. Построена многоуровневая математическая модель конверсии макромолекул в проточном реакторе с учетом эффекта дезактивации катализатора и изменения его порового пространства, на основе уравнений реакции-диффузии и с расчетом изменения параметров порового пространства методами вычислительной геометрии.

Трудность математического описания процесса конверсии макромолекул связана с активным изменением порового пространства катализатора: в результате протекающих реакций частицы кокса оседают на поверхности катализатора. При этом возникает двойной эффект: с одной стороны, оседающие частицы уменьшают активную поверхность, с другой – происходит забивание пор, препятствующее транспорту макромолекул вглубь катализатора. В работе предложена математическая модель, в основе которой уравнения диффузии-реакции замкнуты на параметры изменяющегося порового пространства. При этом в качестве основных характеристик (параметров) порового пространства, характеризующих его эволюцию, рассмотрены пористость, удельная площадь поверхности и извилистость. Рассмотрены четыре уровня масштаба: реактор (уравнение конвекции-диффузии), гранулы (уравнение диффузии-реакции), зерно катализатора, частица кокса (на этих масштабах происходит пространственное моделирование участка катализатора и расчет основных характеристик порового пространства методами вычислительной геометрии). Был проведен численный анализ на примере процесса очистки тяжелой нефти при помощи катализатора на основе оксида алюминия. Показано, что забивание пор (препятствие транспорту макромолекул асфальтена) является лидирующим фактором в процессе дезактивации катализатора. Проведено сравнение мезопористого и макропористого катализаторов и показана более высокая эффективность последнего. Результаты численного эксперимента находятся в высокой степени согласованности с данными реальных экспериментов.

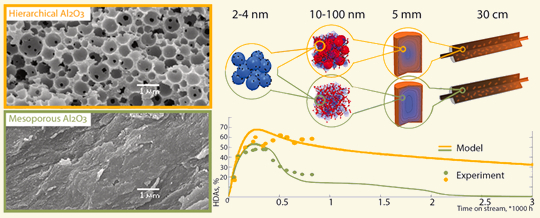
[1] E. V. Parkhomchuk, Ya. V. Bazaikin, E. G. Malkovich, A. I. Lysikov, E. E. Vorobieva, K. V. Fedotov, A. V. Kleymenov. 4-Scale model for macromolecule conversion over mesoporous and hierarchical alumina catalysts // Chemical Engineering Journal, 405 (2021), article id. 126551. https://doi.org/10.1016/j.cej.2020.126551

27. Решена обратная задача по определению газокинетических свойств угля на основе реальных данных.

Апробирован на результатах реальных измерений новый метод интерпретации данных «canister test», позволяющий дать количественную оценку газоносности, коэффициентов диффузии и кинетики десорбции угля. Угольный шлам загружался в специальное измерительное устройство --- канистру, измерялось давления газа (метана), выделившегося из шлама в канистре, по истечении некоторого времени угольный шлам подвергался ситовому анализу с целью определения его гранулометрического состава. Математически прямая задача сводится к системе из двух уравнений: дифференциальному уравнению, описывающего диффузию метана из частички шлама, и интегральному уравнению, описывающему связь связанного и свободного метана в частице. Данные о давлении газа в канистре и гранулометрические параметры шлама служили дополнительной информацией для постановки обратной задачи по определению газокинетических свойств угля. Цель работы – определить газоносность нового пласта угля с целью дальнейшей его разработки. Согласно технике безопасности разработка угольного пласта возможна при содержании метана в нём не более 8 кг/м^3, как правило, в РФ вновь вскрытый угольный пласт имеет газосодержание около 20 кг/м^3.

[1] А. Л. Карчевский, Л. А. Назаров, Л. А. Назарова. Расчет давления газа в закрытой емкости с угольным шламом при изотермической десорбции // Сибирский журнал индустриальной математики, 18:1 (2015), 45-55.
[2] A. L. Karchevsky, L. A. Nazarov, L. A. Nazarova. New method to interpret the ‘canister test’ data for determining kinetic parameters of coalbed gas: theory and experiment // Inverse Problems in Science and Engineering, (2021), DOI: 10.1080/17415985.2021.1936516

28. Аксиоматизирован вектор Шепли в играх с априорными вероятностями образования коалиций.

Предложена и изучается новая модель ТП-игры, в которой помимо стандартной характеристической функции, определяющую игру, используются две дополнительные функции: отношений между игроками и вероятности образования коалиций. Функция отношений определяется как взвешенный граф, вершины которого соответствуют игрокам, а ребра – степени готовности индивидуумов вступить в кооперацию. Для этого класса игр по аналогии с подходом Шепли вводится оригинальное понятие (обобщённого) вектора Шепли, определяющее игровые оценки (ценность) игроков. Предлагается аксиоматизация определённых таким образом «функций значения» на данном классе игр. Доказано, что ей соответствует введённый вектор Шепли и только он (единственность характеризации). Тем самым развита существенно более реалистичная модель кооперативной игры и получено надлежащее обобщение значения игрока - фундаментального понятия Шепли – нобелевского лауреата 2012 года.
На международном уровне работа впервые была представлена на Всемирном конгрессе по Теории Игр 2020, из-за пандемии COVID-19 проходившем в июле 2021 года в Будапеште, Венгрия.

[1] Камионко В. А., Маракулин В. М. Аксиоматизация вектора Шепли в играх с априорными вероятностями образования коалиций // Журнал Новой Экономической Ассоциации, 46:2 (2020), 12-29. DOI: 10.31737/2221-2264-2020-46-2-1

29. Разработана нелинейная модификация классической модели экономического роста. Найдены достаточные условия, гарантирующие поддержание заданного уровня благосостояния (расходов на потребление).

Объектом исследования является динамическая модель функционирования хозяйствующего субъекта. Стратегия развития хозяйствующего субъекта называется рациональной, если благосостояние субъекта превышает некоторый заданный уровень на каждом интервале рассматриваемого временного периода. В 2019 году автором были построены модели для поиска рациональных стратегий, развивающие классическую модель Солоу. Усовершенствованная в 2021 году модель учитывает два новых условия функционирования экономики: (1) требование сохранения заданного уровня благосостояния, а также (2) требование минимизации необходимого уровня производства. Проведен сравнительный анализ рациональных стратегий, полученных в рамках нового подхода, со стратегиями, полученными в рамках классической модели Рамсея-Касса-Купманса. Критериями сравнения являются интегральное благосостояние и интегральный уровень производства. Для случая среднесрочного (до 10 лет) горизонта прогнозирования, показано, что стратегии, полученные в рамках предложенной модели, лучше стратегий, полученных в рамках модели Рамсея-Касса-Купманса, по обоим критериям.

[1] S. M. Antsyz. One Refinement of the Simplest Growth Model // Proceedings of the 17th International Asian School-Seminar “Optimization Problems of Complex Systems” (OPCS 2021). Novosibirsk, Russia: Publisher IEEE Catalog Number: CFP21U46-ART, 2021, pp. 9-12. DOI: 10.1109/OPCS53376.2021.9588768
[2] S. M. Antsyz. On Models of Economic Development, Taking into Account Lending // Proceedings of the 15th International Asian School-Seminar “Optimization Problems of Complex Systems” (OPCS 2019). Novosibirsk, Russia: Publisher IEEE Catalog Number: CFP19U46-ART, 2019, pp. 4-7. DOI: 10.1109/OPCS.2019.8880202
[3] Antsyz S. M., Vysotskaya T. V. About Some Two-level Models of Optimization of Tax Schemes // CEUR Workshop Proceedings, 2018, vol. 2098, pp. 17–32.

30. Описано множество кортежей, являющихся спектрами гамильтоновых циклов в n-кубе.

Спектром гамильтонова цикла (кода Грея) в булевом n-кубе называется кортеж из n чисел, где i-ое число равно количеству ребер i-го направления в цикле. Известны необходимые условия существования гамильтонова цикла с фиксированным спектром: все числа в спектре четные и сумма любых k из них не меньше 2^k. Доказано [1-2], что эти необходимые условия являются достаточными для существования гамильтонова цикла с таким спектром. Это окончательное решение известной задачи, в частности, сформулированной Д. Кнутом в 2009г. в 4-м томе «Искусство программирования». Ранее при перечислении классов эквивалентности кодов Грея задача была решена для n < 7, а в [1], используя различные конструкции кодов Грея, для n = 7 и 8. В 2012 году В.Н.Потапов получил условно асимптотическое решение. В [2] дано полное решение задачи для любой размерности n-куба.

[1] Малых А. Е., Пережогин А. Л. Конструктивный подход к перечислению спектров кодов Грея в булевых кубах малых размерностей // Вестн. НГУ. Серия: Информационные технологии, 15:4 (2017), 32–42.
[2] Perezhogin A. L. On the spectrum of Hamiltonian cycles in the n-cube // Journal of Combinatorial Theory, Series B, 151 (2021), 435–464.

31. На основе типичных свойств метрических шаров, содержащихся в графе, установлен радиус почти всех n-вершинных графов фиксированного диаметра k. Описана структура и спектр центра почти всех n-вершинных графов заданного диаметра k.

Свойство графов рассматриваемого класса типичное, если почти все графы этого класса обладают данным свойством. Изучаются типичные свойства класса n-вершинных графов фиксированного диаметра k. На основе типичных свойств метрических шаров, содержащихся в графе, установлен радиус почти всех n-вершинных графов исследуемых классов. Доказано, что для любого фиксированного k≥3 почти все n-вершинные графы диаметра k имеют радиус ⌈ k/2⌉ , при этом радиус почти всех графов диаметра k=1,2 равен диаметру.
Асимптотически исследован центр и его спектр (множество мощностей центров) n-вершинных графов фиксированного диаметра k. Установлена структура центра почти всех n-вершинных графов диаметра k. При k=1,2 любая вершина является центральной, а для k≥3 выделено два типа центральных вершин, необходимых и достаточных для получения центров почти всех таких графов, при этом для описанного класса типичных графов центр найден явно. Для n-вершинных связных графов описан спектр центра всех и почти всех. Доказано, что центр почти всех n-вершинных графов диаметра k имеет мощность n при k=1,2 и n−2 при k=3, а для k≥4 спектр центра ограничен интервалом из последовательных целых чисел, за исключением не более одного значения (двух значений) вне этого интервала для чётного диаметра k (для нечётного диаметра k) в зависимости от значения k. Установлена реализуемость найденного спектра мощностей центра в классе описанных типичных n-вершинных графов диаметра k. Вычислены ненулевые асимптотические доли числа графов в подклассах, соответствующих случаям значений спектра центра, а также описаны типичные графы для этих подклассов.
Все полученные типичные свойства n-вершинных графов фиксированного диаметра k≥2 остаются типичными и для связных графов диаметра не менее k, а также для графов (не обязательно связных), содержащих кратчайшую цепь длины не менее k.

[1] T. I. Fedoryaeva. On radius and typical properties of n-vertex graphs of given diameter // Siber. Electr. Math. Reports. 18:1 (2021), 345–357. DOI 10.33048/semi.2021.18.024
[2] T. I. Fedoryaeva. Center and its spectrum of almost all n-vertex graphs of given diameter // Siber. Electr. Math. Reports, 18:1 (2021), 511–529. DOI 10.33048/semi.2021.18.037

32. Для задачи упаковки 2-гистограмм в полосу разработаны новые полиномиальные алгоритмы для построения приближенных решений с нетривиальными априорными достижимыми оценками точности.

Множество гистограмм, каждая из которых состоит из двух столбиков, высота которых не более 1, требуется упаковать в полосу высоты 1 минимальной длины. Запрещено переставлять и разрывать столбики одной гистограммы, но они могут произвольно перемещаться вертикально в пределах полосы. Эта новая задача комбинаторной оптимизации, возникшая из приложений, является обобщением классических задач упаковки в контейнеры и задачи двумерной векторной упаковки (откуда следует, в частности, NP-трудность и 3/2-неаппроксимируемость задачи), а также частным случаем задачи календарное планирование с одним возобновляемым ресурсом.
Для произвольных 2-гистограмм разработан полиномиальный приближённый алгоритм, который строит упаковку длины не более 2OPT+1, где OPT – минимальная длина упаковки. Для случая больших гистограмм (когда один из столбиков имеет высоту более 1/2) разработан полиномиальный 3/2-приближённый алгоритм. Кроме априорного, проведен апостериорный анализ разработанных алгоритмов, который показал, что разработанный жадный алгоритм с предварительным лексикографическим упорядочиванием гистограмм в среднем строит решение близкое к оптимальному.


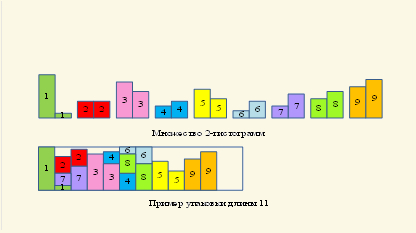
[1] A. Erzin, G. Melidi, S. Nazarenko, R. Plotnikov. Two-Bar Charts Packing Problem // Optimization Letters, 15:6 (2021), 1955-1971. https://doi.org/10.1007/s11590-020-01657-1
[2] A. Erzin, G. Melidi, S. Nazarenko, R. Plotnikov. A 3/2-approximation for big two-bar charts packing // J. of Combinatorial Optimization, 42 (2021), 71–84. https://doi.org/10.1007/s10878-021-00741-1

33. Получен новый полиномиальный алгоритм точного решения классической задачи open shop с двумя машинами, установлена полиномиальная разрешимость двухмашинной задачи с маршрутизацией и выбираемой базой.

Объектом исследования является одна из классических задач теории расписаний, известная под названием "задача открытого типа", или open shop. Задача с двумя машинами полиномиально разрешима, и для неё известно четыре различных алгоритма, которые строят расписания с разными структурными свойствами. Мы предлагаем новый алгоритм точного решения этой задачи. Этот алгоритм отличается от предшествующих как простотой описания и обоснования оптимальности, так и большей свободой в структуре получаемого решения: он позволяет выполнять работы в произвольном порядке с точностью до циклической перестановки. Этот алгоритм позволяет также решить более общую постановку задачи, в которой работы расположены в узлах транспортной сети, и машины затрачивают время на перемещение между узлами. Тем самым мы даём ответ на ранее открытый вопрос об алгоритмической сложности задачи в этой постановке.

[1] Khramova, A. P., Chernykh, I. A new algorithm for the two-machine open shop and the polynomial solvability of a scheduling problem with routing // Journal of Scheduling, 24:4 (2021), 405–412. https://doi.org/10.1007/s10951-021-00694-7

34. Доказана гипотеза Джексона о цикловом покрытии двудольных графов и найдены необходимые условия суперцикличности двудольных графов.

Обозначим через G(m,n,d) класс двудольных графов с долями X и Y, где |X|=m, |Y|=n, и степенью каждой вершины в X не менее d. Джексон в 1981 году доказал, что, если d не меньше m и n<2m-1, то каждый граф H из G(m,n,d) содержит цикл, покрывающий X, и предположил, что это верно если n<3n-5 и граф H двусвязен. В работе доказана гипотеза Джексона. Также показано, что в условиях теоремы Джексона граф H не только содержит цикл длины 2m, но для каждого подмножества A из X с |A|>2 граф H содержит цикл, множество вершин которого в X есть в точности A. Назовем такие графы суперциклическими. Найдены необходимые свойства суперцикличности двудольного графа, и описаны несколько классов графов, для которых эти свойства достаточны.

[1] Kostochka A., Lavrov M., Luo R., Zirlin D. Conditions for a bigraph to be super-cyclic // Electron. J. Combin., 28:1 (2021), paper No. 1.2, 19 pp.
[2] A. Kostochka, Luo R., Zirlin D. Super-pancyclic hypergraphs and bipartite graphs // J. Combin. Theory Ser. B, 145 (2020),
.450-465.

35. В работе найдена минимальная мощность носителя произвольной (2n-3i)-собственной функции графа Хэмминга H(n,3) для всех i ˃ n / 2.

В данной работе рассматривается проблема поиска минимальной мощности носителя произвольной собственной функции с фиксированным собственным числом графа Хэмминга H(n,q). Для q=2 данная проблема была полностью решена Д. С. Кротовым в 2016 году. Недавно в работе [A. Valyuzhenich, K. Vorob'ev, Minimum supports of functions on the Hamming graphs with spectral constraints, Discrete Mathematics 342(5) (2019) 1351-1360] данная проблема была полностью решена для всех q≥3 за исключением случая q=3 и половины собственных значений. В настоящей работе проблема поиска минимальной мощности носителя произвольной собственной функции графа Хэмминга H(n,q) решена для незакрытого случая q=3 и половины собственных значений. Используя данные результаты, также удалось установить минимальный размер 1-совершенных трейдов в графе Хэмминга H(n,3).

[1] A. Valyuzhenich. Eigenfunctions and minimum 1-perfect bitrades in the Hamming graph // Discrete Mathematics, 344:3 (2021), 112228. https://doi.org/10.1016/j.disc.2020.112228

36. Доказано существование базы минимального веса для каждого известного в литературе кватернарного кода Рида-Маллера.

Кватернарные конструкции Плоткина и BQ-Плоткина, порождающие два бесконечных семейства кватернарных кодов Рида-Маллера, были предложены Дж. Пуджолом, Ж. Рифой и Ф.И.Соловьевой в 2009 г. Z4-линейные коды, полученные из этих кватернарных кодов под действием отображения Грея, имеют те же параметры и фундаментальные свойства, что и классические двоичные линейные коды Рида-Маллера.
В цикле работ изучено еще одно фундаментальное свойство семейства кватернарных кодов Рида-Маллера, присущее также двоичным линейным кодам Рида-Маллера: данные кватернарные коды имеют базисы, состоящие из кодовых слов минимального веса. Базисы строятся индуктивно.

[1] Solov’eva F. I. Minimum weight bases for quaternary Reed-Muller codes // Siberian Electronic Mathematical Reports, 18:2 (2021), 1358-1366. DOI 10.33048/semi.2021.18.103

37. Найдена асимптотика числа трансверсалей в латинских гиперкубах, полученных суперпозицией (итерированием) некой бинарной квазигруппы. Для итерированных групп установлено, что главный член этой асимптотики определяется мощностью коммутанта.

Для бинарной квазигруппы G порядка n назовем d-итерированной квазигруппой G[d] (d+1)-мерный латинский гиперкуб, который есть таблица Кэли d-кратной суперпозиции G самой с собой. Диагональ латинского гиперкуба называется трансверсалью, если она содержит все различные символы гиперкуба.

Доказано, что для данной квазигруппы G порядка n итерированные квазигруппы G[d] содержат трансверсаль либо для всех d больших некоторого d_0, либо только для четных d. Кроме того, существует константа r, зависящая только от квазигруппы G, такая, что число трансверсалей в G[d] (если оно отлично от нуля) равно (1+o(1))n!^{d+1}/(r n^{n-1}) при d стремящемся к бесконечности. Если G является группой, то константа r равна мощности ее коммутанта. Сходное асимптотическое поведение числа трансверсалей в итерированных группах фиксированной размерности, но растущего порядка недавно обнаружено в работе [S. Eberhard, F. Manners, R. Mrazovic. An asymptotic for the Hall–Paige conjecture. arXiv:2003.01798, 2020.]

Кроме того, разработанная методика дает асимптотические оценки для числа частичных трансверсалей, кратных трансверсалей (плексов) и других подобных подструктур в итерированных группах и квазигруппах.

[1] Taranenko A. A. Transversals plexes, and multiplexes in iterated quasigroups // Electron. J. Combin., 25:4 (2018), #4.30,
17 p.
[2] Taranenko A. A. Transversals near transversals, and diagonals in iterated groups and quasigroups // Electron. J. Combin., 28:3 (2021), #3.48, 22 p. DOI: 10.37236/9699.

38. Теоретически исследована форма и динамика вихревой линии калибровочного поля в средах с нарушением пространственной чётности.

Решена задача о форме и динамике вихревой линии калибровочного поля в средах с нарушением пространственной чётности. Рассмотрение проведено в рамках нерелятивистской абелевой модели Хиггса, дополненной вкладами, меняющими знак при пространственной инверсии. Показано, что в статическом пределе вихревая линия имеет форму спирали с определённым соотношением между кривизной и кручением. Динамика линии описывается нелинейным уравнением движения, линеаризация которого позволила получить закон дисперсии и поляризацию малых колебаний, распространяющихся вдоль вихревой линии. Показано также, что полученное уравнение движения может быть представлено в виде нелинейного уравнения Шрёдингера с новым типом нелинейности.

[1] A.  A. Kozhevnikov Shape and dynamics of nonrelativistic vortex strings in parity-breaking media // Phys. Rev. D, 103 (2021), 025025.

39. Получены предсказания для сечений и угловых распределений процессов рождения бозона Хиггса и струй адронов на Большом Адронном Коллайдере.

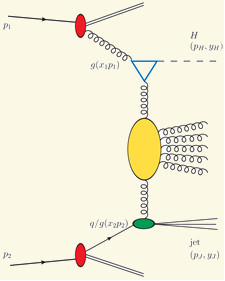
Предлагается исследовать на Большом Адронном Коллайдере (БАК) процессы рождения бозона Хиггса и струй адронов в кинематической области, когда детектируемые бозон Хиггса и струя адронов разделены большим интервалом быстроты. Такие реакции открывают новые возможности для исследования на БАК динамики сильных взаимодействий кварков и глюонов в пределе Редже. Используя метод Балитского-Фадина-Кураева-Липатова, получены предсказания для сечений и угловых распределений этих процессов. Обсуждаются теоретические неопределенности полученных результатов и сравнение с другими подходами.

[1] Celiberto, F. G., Ivanov, D. Y., Mohammed, M.M.A., Papa. A High-energy resummed distributions for the inclusive Higgs-plus-jet production at the LHC // Eur. Phys. J. C, 81 (2021), 293. https://doi.org/10.1140/epjc/s10052-021-09063-2