| |
Важнейшие научные результаты Института математики за 2019 год
1. Построены универсальные обёртывающие алгебры Роты ― Бакстера для пре- и посталгебр в ассоциативном и лиевом случаях.
Алгебры с операторами Роты – Бакстера возникают в различных задачах дискретной математики, анализа, квантовой алгебры и математической физики. Определение операторов Роты – Бакстера формализует свойства операции интегрирования на алгебрах функций. Построены универсальные обёртывающие алгебры Роты – Бакстера для пре- и посталгебр в многообразиях ассоциативных и лиевых алгебр. Получен ответ на вопрос Л. Гуо (2012): пара многообразий (RBAs,postAs) удовлетворяет свойству Пуанкаре – Биркгофа – Витта, а пара многообразий (RBAs,preAs) этому свойству не удовлетворяет. Доказано, что многообразие лиевых алгебр Роты – Бакстера не является шрайеровым.
[1] Gubarev V. Yu. Universal enveloping associative Rota-Baxter algebras of preassociative and postassociative algebra,
J. Algebra, 516 (2018), 298-328.
[2] Губарев В. Ю. Универсальные обёртывающие лиевы алгебры Рота-Бакстера прелиевых и постлиевых алгебр, Алгебра и Логика, 58:1 (2019), 3-21.
2. Описано строение локально конечных групп конечной централизаторной размерности.
Группа G имеет конечную централизаторную размерность k, если длина любой цепи строго вложенных централизаторов в группе
G не превосходит k. Изучалась справедливость следующей гипотезы Боровика – Хухро.
Гипотеза. Пусть G - локально конечная группа конечной централизаторной размерности k. Пусть S - полный прообраз обобщенной подгруппы Фиттинга группы G/F(G). Тогда
1) количество неабелевых композиционных факторов группы G конечно и ограничено в терминах k;
2) группа G/S содержит абелеву подгруппу, чей индекс ограничен в терминах k.
Показана справедливость первой части гипотезы. Кроме того, опровергнута вторая часть гипотезы и доказана справедливость её ослабленной версии. Более точно, показано, что вторая часть гипотезы становится справедливой, если в определении подгруппы S заменить G/F(G) на факторгруппу G по второй подгруппе Фиттинга. Также показано, что если G - это локально конечная группа централизаторной размерности k и R - это её локально разрешимый радикал, то централизаторная размерность фактора G/R ограничена в терминах k.
[1] А. А. Бутурлакин, А. В. Васильев О локально конечных группах с ограниченными рядами централизаторов, Алгебра и логика, 52:5 (2013), 553–558. doi: 10.1007/s10469-013-9248-3
[2] A. A. Buturlakin, D. O. Revin, A. V. Vasil’ev. Groups with bounded centralizer chains and the Borovik-Khukhro conjecture,
J. Group Theory, 21:6 (2018), 1095–1110. doi: 10.1515/jgth-2018-0026
[3] A. A. Buturlakin. The structure of locally finite groups of finite c-dimension, J. of Algebra and its Applications, 18:12 (2019), 1950223. doi: 10.1142/S0219498819502232
3. Доказана справедливость гипотезы Шалева для линейных и унитарных групп.
Напомним, что известная гипотеза Варинга (Waring conjecture) состоит в том, что для любого натурального k существует n (зависящее от k) такие, что любое целое число может быть представлено в виде суммы не более, чем
n слагаемых k-ых степеней целых чисел, т.е.

В таком виде положительное решение этой гипотезы получено Д. Гильбертом. Однако полученное им значение числа n далеко от оптимального. Кроме того, появилось много похожих по формулировке гипотез, решение которых до сих пор не получено. Данное направление в теории чисел получило отдельный код в известной классификации Американского математического общества: 11P05 Waring's problem and variants.
Аналогичные вопросы представляют интерес для других алгебраических систем, в частности для групп. В нашем докладе мы обсудим прогресс в данном направлении в группах, а также представим недавний результат, решающий гипотезу Шалева для линейных и унитарных групп.
[1] Alexey Galt, Amit Kulshrestha, Anupam Singh and Evgeny Vdovin. On Shalev’s conjecture for type An and 2An, Journal of Group Theory, 22:4 (2019), 713-728. DOI: 10.1515/jgth-2018-0142
4. Предложен подход к построению спектральной теории частично упорядоченных множеств.
Предложен подход к построению спектральной теории частично упорядоченных множеств, позволяющий обобщить классическую спектральную теорию (полу)решеток и опирающийся на введенное авторами понятие идеала ч.у.множества.
В рамках этого подхода найдены достаточные условия для изоморфности расширений топологических пространств. Кроме этого получено обобщение теоремы Хоффманна-Мислова, получена характеризация собранных пространств как спектров ч.у. множеств с топологией, получено описание существенных пополнений ч.у. множеств с топологией.
[1] Ю. Л. Ершов, М. В. Швидефски. К спектральной теории частично упорядоченных множеств, Сибирский математический журнал, 60:3 (2019), 578-598.
5. Доказана невложимость первого несчетного ординала ни в какой сигма-определимый предпорядок в наследственно-конечной надстройке над вещественными числами.
Доказано, что первый несчетный ординал не вложим ни в один предпорядок, сигма-определимый с параметрами в наследственно конечной надстройке над вещественными числами. Как следствие, получено полное описание для сигма-представимых над этой надстройкой ординалов,
гёделевских конструктивных множеств, а также доказана невозможность таких представлений для ряда структур степеней алгоритмических сводимостей.
[1] Морозов А. С. О Σ-определимых предпорядках в HF(R), Алгебра и логика, 58:6 (2019), 1324-1334.
6. Доказано, что класс структур, представимых с помощью конечных автоматов, имеет максимально возможную алгоритмическую сложность. Тем самым получен ответ на вопрос А. Нероуда и Б. Хусаинова.
Алгебраическая структура называется автоматной, если её носитель, сигнатурные предикаты и графики сигнатурных функций являются регулярными языками. Автоматные структуры играют важную роль в теоретической информатике. Одна из главных особенностей этих структур заключается в следующем: любая автоматная структура сильно конструктивна, т.е. существует алгоритм, осуществляющий проверку истинности формул логики первого порядка в структуре.
А. Нероуд и Б. Хусаинов поставили вопрос о том, существует ли достаточно простое синтаксическое описание для класса структур, имеющих автоматные представления. В работе доказано, что индексное множество данного класса структур является
 -полным. Тем самым установлено, что данный класс не имеет синтаксического описания в языке вычислимых бесконечных формул. -полным. Тем самым установлено, что данный класс не имеет синтаксического описания в языке вычислимых бесконечных формул.
[1] Bazhenov N., Harrison-Trainor M., Kalimullin I., Melnikov A., Ng K. M. Automatic and polynomial-time algebraic structures, Journal of Symbolic Logic, (2019), published online, doi: 10.1017/jsl.2019.26.
7. Установлена алгоритмическая сложность языка формул с ограниченными кванторами, расширенного термами, отражающими операторы рекурсии по списку, итерации, ограниченной константой, и поиска по спискам.
В рамках парадигмы Семантического программирования, предложенной в работах С. С. Гончарова, Ю. Л. Ершова, Д. И. Свириденко, решен вопрос об алгоритмической сложности расширений языка
Δ0-формул с помощью термов, отражающих операторы рекурсии по списку, итерации, ограниченной константой, и поиска по спискам. Доказано, что множество Δ0-формул, расширенных рекурсивными термами,
истинных в заданной списочной надстройке HW(M) неэлементарно (содержит класс kEXPTIME для любого k≥1). В частности, из этого следует, что данное расширение неконсервативно. Для Δ0-формул, расширенных термами константно ограниченной итерации, проблема истинности в заданной HW(M) NEXPTIME-трудна и лежит в классе 2EXPTIME, если константа задана в бинарном представлении. Расширение с помощью термов списочного поиска консервативно и проблема истинности Δ0-формул с такими термами в заданной структуре HW(M)
является PSPACE-полной. Показано, что любая функция, полиномиально вычислимая по времени, является Δ0-определимой в расширении с помощью термов, реализующих полиномиально ограниченную итерацию.
[1] S. Ospichev, D. Ponomarev. On the complexity of formulas in semantic programming, Siberian Electronic Mathematical Reports, 15 (2018), 987–995.
[2] Гончаров С. С., Свириденко Д. И. Рекурсивные термы в семантическом программировании, СМЖ, 59:6 (2018),
1279-1290.
[3] Гончаров С. С. Условные термы в семантическом программировании, Сиб. мат. журн., 58:5 (2017), 1026-1034.
[4] Гончаров С. С., Свириденко Д. И. Логический язык описания полиномиальной вычислимости, Доклады академии наук, 485:11 (2019), 11–14.
8. Установлено, что если мультипликативная группа двустороннего брэйса нильпотентна ступени k, то аддитивная группа этого брэйса разрешима ступени не более 2k.
Брэйсом называется алгебраическая система с двумя групповыми операциями (сложение и умножение), связанными между собой одним конкретным соотношением. Брэйсы были построены Румпом как мощный инструмент для конструирования решений теоретико множественного уравнения Янга-Бакстера (уравнение Янга-Бакстера имеет собственный индекс предметной классификации MSC2010 – 16T25). Румп установил, что любое инволютивное решение теоретико-множественного уравнения Янга-Бакстера может быть построено с помощью некоторого брэйса. Так алгебраические свойства брэйсов играют важную роль при изучении свойств решений теоретико множественного уравнения Янга-Бакстера.
Используя классификацию конечных простых групп, Бийотт установил, что если мультиплекативная группа конечного брэйса абелева, то аддитивная группа этого брэйса разрешима. В работе автора установлено, что если мультиплекативная группа двухстороннего брэйса (специальный вид брэйсов) нильпотентна ступени k, то аддитивная группа этого брэйса разрешима ступени не более 2k. Так как брэйс с абелевой мультиплекативной группой является двухсторонним, предлагаемый результат существенно усиливает результат Бийотта: он справедлив не только для конечных брэйсов, он дает верхнюю оценку на ступень разрешимости, он не использует классификации конечных простых групп.
Результат частично отвечает на гипотезу Вендрамина-Смоктунович.
[1] T. Nasybullov. Connections between properties of the additive and the multiplicative groups of a two-sided skew brace,
J. Algebra, 540 (2019), 156–167.
9. Построены представления группы виртуальных кос в группу автоморфизмов свободного произведения свободной и свободной абелевой группы, которые обобщают все известные ранее представления.
Одним из обобщений классической группы кос является группа виртуальных кос, играющая ту же роль в теории виртуальных узлов, какую классическая группа кос играет в теории классических узлов. Представление Артина классической группы кос в группу автоморфизмов свободной группы позволяет решить проблему равенства слов в группе кос, построить линейное представление группы кос (представление Бурау), линейное представление группы крашеных кос (представление Гасснера), найти группу классического зацепления и т.д. Авторами построены представления группы виртуальных кос в группу автоморфизмов свободного произведения свободной и свободной абелевой группы.
Построенные представления обобщают все известные ранее представления.
[1] Bardakov V. G., Mikhalchishina Yu. A., Neshchadim M. V. Representations of virtual braids by automorphisms and virtual knot groups. Journal of Knot Theory and Its Ramifications. Vol. 26 (2017) 1750003 (17 pages).
[2] Бардаков В. Г., Нещадим М. В. Об одном представлении виртуальных кос автоморфизмами. Алгебра и Логика. 56,
№ 5(2017), 539-547.
[3] Бардаков В. Г., Михальчишина Ю. А., Нещадим М. В. Группы виртуальных зацеплений. СМЖ, Т. 58, № 5(2017),
стр. 989-1003.
[4] V. G. Bardakov, Yu. A. Mikhalchishina, M. V. Neshchadim. Groups of the virtual trefoil and Kishino knots. Journal of Knot Theory and Its Ramifications. Vol. 27, No. 13, 1842009 (2018).
[5] Bardakov V. G., Neshchadim M. V. Knot Groups and Residual Nilpotence. Proceedings of the Steklov Institute of Mathematics, 2019, Vol. 304, Suppl. 1, pp. 23-30.
10. Получены достаточные условия однородности геодезической и новое доказательство геодезической орбитальности слабо симметрических пространств для римановых многообразий. Исследования введенных и изученных ранее авторами для римановых многообразий классов однородных пространств распространены на конечные метрические пространства.
Устанавливается достаточное условие для того, чтобы геодезическая в римановом многообразии была однородной, т.е. чтобы она была орбитой однопараметрической группы движений.
На основе этого дается новое доказательство важной теоремы о том, что слабо симметрическое по Сельбергу риманово многообразие геодезически орбитально, т.е. каждая его геодезическая однородна.
Также изучаются общие свойства однородных геодезических римановых многообразий, в частности, структура замыкания данной однородной геодезической. Представлено несколько примеров, когда это замыкание – многомерный тор, который может быть, а может и не быть вполне геодезическим подмногообразием.
В конце обсуждаются однородные геодезические с необычными свойствами на группах Ли с левоинвариантной римановой метрикой. По предложению В. Н. Берестовского изучались класс конечных однородных метрических пространств и его важные шесть подклассов, имеющих естественные определения в терминах метрики и хорошо изученные ранее М. Берже и авторами аналоги в классе однородных римановых многообразий.
Исследованы взаимоотношения между этими подклассами. Строятся примеры соответствующих пространств, часть которых представляют собой множества вершин специальных выпуклых (в том числе правильных и полуправильных) многогранников в евклидовых пространствах. Даются описания изучаемых классов на языке множеств левых смежных классов конечных групп по их подгруппам и теории графов (в том числе графов Кнезера), с помощью которых строятся необычные примеры конечных однородных метрических пространств.
Введены операции прямого произведения (сохраняющего все подклассы) и раздутия, а также понятия локального графа и раскрашенного графа для таких пространств.
Есть интересные перспективы дальнейшего изучения этих пространств. Так, еще не изучены допускающие естественные определения подклассы симметрических и слабо симметрических конечных метрических пространств, принадлежность множеств вершин правильных и полуправильных многогранников в евклидовых пространствах высших размерностей упомянутым подклассам, инвариантность подклассов относительно более общей операции прямого произведения (которую ввели С. Августинович и Д. Фон-Дер-Флаасс),
наконец, возможность естественной метризации (еще не метризованных) конечных аналогов (обобщенных) симметрических пространств, так называемых конечных quandles. Их ввел D. Joyce в 1982 г. как множества с бинарными операциями, удовлетворяющими трем аксиомам, соответствующим перестройкам Рейдемейстера классических узлов.
В трех статьях 2013 и 2016 гг. H. Tamaru с соавторами изучали соответственно двухточечно однородные, цикличные и плоские связные конечные quandles.
[1] Berestovskii V. N., Nikonorov Yu. G. On homogeneous geodesics and weakly symmetric spaces, Annals of Global Analysis and Geometry, 55 (2019), 575-589. Doi: 10.1007/s10455-018-9641-1
[2] Берестовский В. Н., Никоноров Ю. Г. Конечные однородные метрические пространства, Сибирский математический журнал, 60:5 (2019), 973-995. DOI: 10.33048/smzh.2019.60.502
[3] Berestovskii V. N., Nikonorov Yu. G. Finite homogeneous metric spaces, Siberian Mathematical Journal, 60:5 (2019), 757-773.
11. Доказано, что наличие у магнитного геодезического потока на двумерном торе полиномиального по импульсам первого интеграла произвольной степени на достаточно большом количестве различных уровней энергии влечет существование линейного первого интеграла на всех уровнях.
Исследуется вопрос о существовании аналитических римановых метрик на двумерном торе, геодезический поток которых в ненулевом магнитном поле вполне интегрируем в классе полиномиальных по импульсам первых интегралов.
В немногочисленных известных примерах дополнительный первый интеграл является либо линейным (на всех уровнях энергии), либо квадратичным (при фиксированном уровне энергии). Недавно И. А. Тайманов доказал, что квадратичный первый интеграл на двух различных уровнях энергии всегда сводится к линейному.
Получено обобщение этого результата. А именно, доказано, что если существует полиномиальный по импульсам первый интеграл произвольной степени на достаточно большом количестве различных уровней энергии, то обязательно существует линейный первый интеграл на всех уровнях.
[1] Agapov S., Valyuzhenich A. Polynomial integrals of magnetic geodesic flows on the 2-torus on several energy levels, Discrete and Continuous Dynamical Systems, Series A, 39:11 (2019), 6565-6583.
12. Успешно решена проблема распространения свойства квазимёбиусовости на случай неоднолистных и неоднозначных отображений в птолемеевых мёбиусовых структурах.
В птолемеевых мёбиусовых структурах (в смысле С. В. Буяло) рассмотрены классы многозначных отображений с контролируемым искажением обобщённых углов. Для них доказаны теоремы непрерывности, теоремы типа Пикара, теоремы о принадлежности этому классу обратных (многозначных) отображений к координатным вектор-функциям квазирегулярных отображений эвклидовых пространств.
Доказана теорема о совпадении подкласса однозначных отображений этого типа с классом квазимёбиусовых отображений, введенных Ю. Вяйсяля с целью распространения свойства квазиконформности на отображения произвольных полуметрических пространств. Полученные результаты позволяют считать, что успешно решена проблема распространения свойства квазимёбиусовости на случай неоднолистных и неоднозначных отображений в птолемеевых мёбиусовых структурах.
[1] Aseev V. V. On coordinate vector-functions of quasiregular mappings // Siberian Electron. Math. Reports, 2018, V.15,
p. 768-772.
[2] Асеев В. В. Обобщенные углы в птолемеевых мëбиусовых структурах. II, СМЖ, 59:5 (2018), 976–987.
[3] Асеев В. В. Обобщенные углы в птолемеевых мëбиусовых структурах, СМЖ, 59:2 (2018), 241–256.
[4] Aсеев В. В. Многозначные отображения со свойством квазимёбиусовости // Сибирский математич. журнал, 2019,
т. 60,№ 6, с. 953-973.
13. Установлена формула площади для классов отображений пространств Карно- Каратеодори, являющихся гёльдеровыми в субримановом смысле.
Рассмотрены классы гёльдеровых отображений пространств Карно-Каратеодори, а именно, отображения-графики и гладкие (в римановом смысле) отображения. Для соответствующих поверхностей-образов выведено несколько видов формулы площади. В качестве одного из шагов исследован аналог параллельного переноса, и показано, что полученные дифференциальные свойства этого аналога неулучшаемы. Кроме того, установлена структура полиномиального субриманова дифференциала для поверхностей-графиков.
[1] Карманова М. Б. О классе гёльдеровых поверхностей на пространствах Карно-Каратеодори, Сибирский математический журнал, 60:5 (2019), 1103–1132.
14. Решена обобщённая проблема Соболева-Решетняка о допустимых заменах переменной для функций с первыми обобщёнными производными на римановых многообразиях.
Получено описание метрических свойств измеримых отображений областей̆ на римановых многообразиях, индуцирующих по правилу композиции изоморфизмы пространств Соболева. Доказано, что всякое такое отображение можно переопределить на множестве нулевой̆ меры так, что оно будет квазиизометрическим, когда показатель суммируемости отличен от размерности риманова многообразия, либо совпадать с квазиконформным отображением в противном случае.
[1] Водопьянов С. К. О допустимых заменах переменных для функций классов Соболева на (суб)римановых многообразиях, Докл. АН, 468:6 (2016), 609–613.
[2] Водопьянов С. К. Допустимые замены переменных для функций классов Соболева на (суб)римановых многообразиях, Мат. сб., 210:1 (2019), 63–112.
[3] Водопьянов С. К. Изоморфизмы соболевских пространств на римановых многообразиях и квазиконформные отображения, Сиб. Мат. журн., 60:5 (2019), 996-1034.
15. Разработан метод исследования геометрических характеристик эквирегулярного субриманова многообразия по диагональной асимптотике его ядра теплопроводности.
В настоящей работе фундаментальное решение уравнения теплопроводности с сублапласианом исследуется при помощи метода возмущений, который сводит исходное уравнение к аналогичному уравнению, но для нильпотентной аппроксимации; для решения последнего мы используем теорию представлений и метод орбит Кириллова. При некотором дополнительном предположении полученные таким образом формулы дают выражение для диагональной асимптотики ядра теплопроводности в субримановом многообразии в терминах его горизонтального распределения, а также коприсоединённых орбит группы Ли, являющейся его нильпотентной аппроксимацией. Рассмотрен конкретный пример многообразия, нильпотентной аппроксимацией которого является группа Гурса.
[1] Кузнецов М. В. Применение нильпотентной аппроксимации и метода орбит для поиска диагональной асимптотики субримановых ядер теплопроводности, Сиб. мат. журн., 60:6 (2019), 1350-1378.
16. Показана взаимосвязь и найдены условия эквивалентности задачи R-линейного сопряжения и усеченного уравнения Винера – Хопфа.
В работах [1, 2] впервые показана взаимосвязь и найдены условия эквивалентности задачи R-линейного сопряжения (известной также под названием задачи Маркушевича и обобщенной краевой задачи Римана) и интегрального уравнения в свертках второго рода на конечном интервале (известного также под названием усеченного уравнения Винера – Хопфа).
В качестве следствия выявленной взаимосвязи в работе [3] получены новые условия корректной разрешимости задачи R-линейного сопряжения и усеченного уравнения Винера – Хопфа.
[1] Воронин А. Ф. О связи обобщенной краевой задачи Римана и усеченного уравнения Винера — Хопфа, СЭМИ, 15 (2018), 412-421.
[2] Воронин А. Ф. Обобщенная краевая задача Римана и интегральные уравнения в свертках первого и второго рода на конечном интервале, СЭМИ, 15 (2018), 611-623.
[3] Воронин А. Ф. Исследование задачи R-линейного сопряжения и усеченного уравнения Винера-Хопфа, Математические труды, 22:2 (2019), 21-33.
17. Бесфазовые обратные задачи для уравнений электродинамики сведены к хорошо изученной обратной кинематической задаче, что открывает путь их конструктивного решения.
Для непроводящей среды рассматриваются периодические по времени высокочастотные электромагнитные колебания, вызванные точечными источниками тока или плоскими волнами, идущими из бесконечности. Изучаются задачи об определении переменного коэффициента диэлектрической проницаемости по заданному на некотором множестве модулю вектора электрической напряженности поля (рассеянного на неоднородности среды, либо полного). Подобные задачи возникают при изучении наноструктуры веществ или биологических клеток. Установлено, что рассматриваемые задачи сводятся к хорошо изученной обратной кинематической задаче, что открывает путь их конструктивного решения. Полученные результаты имеют приоритетный характер.
[1] Романов В. Г. Задача об определении коэффициента диэлектрической проницаемости в стационарной системе уравнений Максвелла, Доклады АН, 474:4 (2017), 413-417.
[2] Романов В. Г. Задача об определении коэффициента диэлектрической проницаемости по модулю рассеянного электромагнитного поля, Сиб. матем. журн., 58:4 (2017), 916-924.
[3] Романов В. Г. Обратные задачи без фазовой информации, использующие интерференцию волн, Сиб. матем. журн.,
59:3 (2018), 626-638.
[4] Романов В. Г. Определение диэлектрической проницаемости по модулю вектора электрической напряженности высокочастотного электромагнитного поля, Доклады АН, 484:3 (2019), 269-272.
[5] Романов В. Г. О решениях уравнений Максвелла, инициируемых плоскими волнами в анизотропной среде, Сиб. матем. журн., 60:4 (2019), 845-859.
[6] Романов В. Г. Обратная бесфазовая задача для уравнений электродинамики в анизотропной среде, Доклады АН,
488:4 (2019), 365-368.
18. Установлено, что принадлежащая полю экстремаль доставляет минимум вариационному функционалу в классе функций с теми же граничными данными и графиком, лежащим в покрытом полем множестве.
Доказан основной результат теории поля для произвольного поля экстремалей без каких-либо дополнительных ограничений. Установлено, что если экстремаль принадлежит полю, то она доставляет минимум вариационному функционалу в классе функций с теми же граничными данными и с графиком, принадлежащим покрытому полем множеству. Ранее этот результат доказывался при дополнительных ограничениях в контексте теории поля Вейерштрасса−Гильберта. Теперь в теории поля предлагается прямой метод. Основной результат использует теорию регулярности решений в вариационных задачах минимизации с препятствиями.
[1] М. А. Сычев. Вариационная теория поля с точки зрения прямых методов, Сибирский математический журнал, 58:5 (2017), 1150-1158. DOI: 10.17377/smzh.2017.58.516
[2] R. Gratwick, M. A. Sychev. One-dimensional variational obstacle problems, Pure and Applied Functional Analysis, 4:3 (2019), 547-558.
19. Для первой краевой задачи для анизотропного параболического уравнения с градиентными нелинейностями доказано существование вязкого в смысле Лионса решения, непрерывного по Липшицу по пространственным переменным и непрерывного по Гёльдеру по времени.
Рассмотрена первая начально-краевая задача для анизотропного параболического уравнения с зависящими от времени показателями
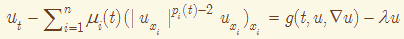 в цилиндре в цилиндре  , ,
где  , а функция , а функция  имеет произвольный рост по градиенту на бесконечности. Цель работы заключалась в построении решений, непрерывных по Липшицу по пространственным переменным. Но присутствие градиентных нелинейностей не позволяет построить обобщенные решения в соболевском смысле, обладающие указанной гладкостью. Главной проблемой является предельный переход в нелинейном градиентном члене в последовательности классических решений регуляризованных задач, аппроксимирующих решение исходной задачи. Для решения этой проблемы привлечен аппарат теории вязких по Лионсу решений, позволивший избежать предельного перехода в градиентных членах и доказать теорему существования даже при градиентных нелинейностях, не удовлетворяющих условию Бернштейна. имеет произвольный рост по градиенту на бесконечности. Цель работы заключалась в построении решений, непрерывных по Липшицу по пространственным переменным. Но присутствие градиентных нелинейностей не позволяет построить обобщенные решения в соболевском смысле, обладающие указанной гладкостью. Главной проблемой является предельный переход в нелинейном градиентном члене в последовательности классических решений регуляризованных задач, аппроксимирующих решение исходной задачи. Для решения этой проблемы привлечен аппарат теории вязких по Лионсу решений, позволивший избежать предельного перехода в градиентных членах и доказать теорему существования даже при градиентных нелинейностях, не удовлетворяющих условию Бернштейна.
[1] Alkis S. Tersenov, Aris S. Tersenov. Existence results for anisotropic quasilinear parabolic equations with time-dependent exponents and gradient term, Journal of Mathematical Analysis and Applications, 480:1 (2019), 123386.
DOI: 10.1016/j.jmaa.2019.123386
20. Получены новые функциональные предельные теоремы для обобщенных процессов восстановления.
Получено обобщение известной теоремы Анскомбе о сходимости случайных величин на случай сходимости стохастических процессов. С его помощью для обобщенных процессов восстановления (о.п.в.) в случае конечных дисперсий элементов управляющей последовательности удается получить принцип инвариантности. Установлено, что в случае бесконечных дисперсий слабая сходимость о.п.в. к устойчивым процессам относительно метрики Скорохода в том виде, в каком она имела место для случайных блужданий, отсутствует. В этом случае (а) найдено дополнительное условие (близкое к минимальному), при котором установлена слабая сходимость о.п.в. к устойчивому процессу; (б) найдена естественная метрика в пространстве
D, относительно которой имеет место слабая сходимость о.п.в. к устойчивому процессу при очень широких (так же, по-видимому, минимальных) условиях, однако эти условия все же оказываются более ограничительными по сравнению с условиями сходимости распределений в фазовом пространстве.
[1] Боровков А. А. Функциональные предельные теоремы для обобщенных процессов восстановления, Сибирский математический журнал, 60:1 (2019), 37-53.
DOI: 10.33048/smzh.2019.60.104
21. Доказано, что вопрос о хорошей обусловленности системы уравнений для построения интерполяционного сплайна через коэффициенты разложения k-й производной по B-сплайнам эквивалентен вопросу сходимости процесса интерполяции для k-й производной сплайна в классе функций с непрерывной k-й производно.
Рассматривается классическая задача интерполяции полиномиальными сплайнами минимального дефекта. Такие сплайны являются нелокальными и поэтому их вычисление требует решения каких-либо систем линейных уравнений. Ранее автором был предложен и изучен подход к построению интерполяционных сплайнов, состоящий в нахождении коэффициентов представления какой-либо производной искомого сплайна в базисе из
B-сплайнов. Были выписаны системы линейных уравнений относительно таких коэффициентов, изучены свойства матриц этих систем. Установлены оценки величины функции погрешности и производных через нормы обратных матриц выписанных систем уравнений. Таким образом, возможность «хорошей» оценки нормы обратной матрицы независимо от сетки позволяет установить соответствующую сходимость интерполяционного процесса. И наоборот, расходимость процесса интерполяции на какой-либо последовательности сеток означает плохую обусловленность матрицы системы уравнений, возникающей при построении сплайна.
Возник естественный вопрос: можно ли из сходимости процесса интерполяции говорить о хорошей обусловленности матрицы и оценке нормы ее обратной независимо от сетки? В настоящем исследовании установлено, что возможность оценки независимо от сетки норм обратных матриц рассматриваемых ранее систем уравнений для определения коэффициентов разложения какой-либо производной определяемого сплайна эквивалентна сходимости процесса сплайн-интерполяции для соответствующих производных. Результаты получены как для классических сплайнов нечётной степени, так и для менее распространённых сплайнов чётной степени.
[1] Волков Ю. С. Сходимость процессов сплайн-интерполяции и обусловленность систем уравнений построения сплайнов, Математический сборник, 210:4 (2019), 87-102.
[2] Волков Ю. С. Изучение сходимости процессов интерполяции для сплайнов чётной степени, Сибирский математический журнал, 60:6 (2019), 1247-1259.
22. В модели монополистической конкуренции с инвестициями в НИОКР получена сравнительная статика рыночного равновесия и общественной оптимальности по размеру рынка и некоторым другим параметрам модели.
Исследуется модель монополистической конкуренции с аддитивно сепарабельной функцией полезности потребителей. Предполагается, в отличие от традиционных постановок с линейной функцией издержек производителей, что предельные издержки не постоянны, а являются убывающей функцией от фиксированных издержек (инвестиций в НИОКР). При этом невозможно получить явный вид состояний рыночного равновесия и общественной оптимальности. Удалось изучить поведение при малом изменении параметров модели (локальную сравнительную статику) состояний равновесия и оптимальности по размеру рынка, а также по некоторым другим параметрам.
[1] Bykadorov I. Monopolistic competition with investments in productivity, Optimization Letters, 13:8 (2019), 1803–1817.
DOI: 10.1007/s11590-018-1336-9
[2] Bykadorov I., Kokovin S. Can a larger market foster R&D under monopolistic competition with variable mark-ups?, Research in Economics, 71:4 (2017), 663-674. DOI: 10.1016/j.rie.2017.10.006
[3] Bykadorov I. Monopolistic Competition Model with Different Technological Innovation and Consumer Utility Levels, CEUR Workshop Proceedings, 1987 (2017), 108-114.
23. Теорема Скарфа о ядре обобщена на случай нечетких кооперативных игр без побочных платежей, когда блокирование усиливается за счет нечетких коалиций.
Предлагается обобщение известной теоремы Скарфа о непустоте ядра на случай нечетких кооперативных игр без побочных платежей, когда блокирование усиливается за счет нечетких коалиций. Использование подходящей аппроксимации нечеткой игры конечнопорожденными играми и применение комбинаторной леммы Скарфа об ординальных и допустимых базисах позволяет установить достаточно общие условия существования неблокируемых дележей для F-сбалансированных нечетких игр. Полученные обобщения теоремы Скарфа применяются для доказательства непустоты нечетких ядер некоторых классических моделей рынка.
[1] Васильев В. А. Неблокируемые дележи нечетких игр II. Непустота ядер двух игр рынка, Сибирский журнал чистой и прикладной математики, 18:4 (2018), 3–18. DOI: 10.33048/pam.2018.18.401
[2] Васильев В. А. Неблокируемые дележи нечетких игр I. Существование, Сибирский журнал чистой и прикладной математики, 18:1 (2018), 35–53. DOI: 10.17377/PAM.2018.18.4
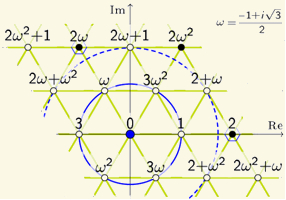
24. В графах Дуба получена характеризация максимальных дистанционно разделимых кодов (с точностью до эквивалентности), и совершенных кодов (линейных – с точностью до эквивалентности, аддитивных и произвольных – с точностью до параметров).
Граф D(M,N), задающий соответствующую метрическую схему отношений, определяется как декартово произведение
M копий графа Шрикханде и N копий полного графа K4. При M=0 это известный граф Хэмминга H(N,4), а при
M>0 известен как граф Дуба, дистанционно регулярный граф с теми же параметрами что и H(2M+N,4). Если вершинам графа Шрикханде сопоставить элементами фактор-кольца
GR(42) кольца целых комплексных чисел Эйзенштейна по модулю 4 (рис.), то вершины графа Дуба образуют модуль над этим кольцом. В серии работ описаны все возможные максимальные дистанционно разделимые (лежащие на границе Синглтона) коды, включая два бесконечных семейства кодов с минимальным расстоянием 2 [2] и 2M+N [4] и конечное число кодов с расстояниям 3 и 4 [4], все линейные (образующие подмодуль) совершенные коды [5], все параметры аддитивных (замкнутых относительно сложения) [1] и произвольных (не обязательно линейных или аддитивных) [3] совершенных кодов.
[1] M. Shi, D. Huang, D. Krotov Additive perfect codes in Doob graphs, Designs, Codes and Cryptography, 87:8 (2019),
1857-1869.
[2] D. S. Krotov, E. A. Bespalov Distance-2 MDS codes and latin colorings in the Doob graphs, Graphs and Combinatorics,
34:5 (2018), 1001-1017.
[3] D. S. Krotov Existence of perfect codes in Doob graphs, Proc. 16th Int. Workshop on Algebraic and Combinatorial Coding Theory (ACCT-XVI), Svetlogorsk , Russia, 2-8 Sept. 2018, 9-13.
[4] Е. А. Беспалов, Д. С. Кротов МДР-коды в графах Дуба, Проблемы передачи информации, 53:2 (2017), 40-59.
[5] D. S. Krotov Perfect Codes in Doob Graphs, Designs, Codes and Cryptography, 80:1 (2016), 91-102.
25. Найдена минимальная мощность носителя произвольной собственной функции с любым заданным собственным значением графа Хэмминга H(n,q) для q>3, а также в случае q=3 для половины собственных значений графа. Кроме того, для q>4 получена характеризация собственных функций с минимальной мощностью носителя.
В данном цикле работ рассматривается проблема поиска минимальной мощности носителя, или другими словами, числа ненулевых значений произвольной собственной функции с фиксированным собственным числом графа Хэмминга
H(n,q). Для q=2 данная проблема была полностью решена Потаповым в 2012 году. В настоящей работе данная проблема полностью решена для
q>2 за исключением случая q=3 и половины собственных значений. Помимо этого, для
q>4 получена характеризация собственных функций с минимальной мощностью носителя в терминах тензорного произведения элементарных собственных функций, определенных на графах Хэмминга диаметра один или два. Отметим, что хотя изначальная задача формулировалась для функций с произвольными действительными значениями, оказалось, что собственные функции с минимальным носителем принимают только три различных значения. Кроме того, получены результаты не только для собственных функций, но и для функций из прямой суммы собственных подпространств, соответствующих нескольким последовательным собственным значениям.
[1] A. Valyuzhenich Minimum supports of eigenfunctions of Hamming graphs, Discrete Mathematics, 340:5 (2017), 1064-1068. doi: 10.1016/j.disc.2016.09.018
[2] A. Valyuzhenich, K. Vorob'ev Minimum supports of functions on the Hamming graphs with spectral constraints, Discrete Mathematics, 342:5 (2019), 1351-1360. doi: 10.1016/j.disc.2019.01.015
26. Доказано, что при n = 3, 5 и при n, равном степени двойки, любое минимальное правильное разбиение множества рёбер n- мерного куба является совершенным.
Результат относится к области теории сложности и связан с известной трудной проблемой получения нижних оценок сложности схем, реализующих конкретные булевы функции. Идеальным решением этой проблемы представляется не просто получение точной (совпадающей с верхней) нижней оценки, но описание класса всех минимальных схем, реализующих данную функцию. Следствием вышеуказанного результата (как было установлено ранее) как раз и является описание классов всех минимальных параллельно-последовательных контактных схем (π-схем), реализующих линейные булевы функции, существенно зависящие от
n переменных при соответствующих (3, 5, 2k) значениях n. Более точно, этими π-схемами являются π-схемы, построенные по несколько обобщённому правилу С. В. Яблонского, и только они.
[1] Рычков К. Л. О совершенности минимальных правильных разбиений множества ребер n-мерного куба, Дискретный анализ и исследование операций, 26:4 (2019), 74-107.
27. Построен бесконечный класс 2-транзитивных разбиений пространства всех двоичных векторов над полем Галуа GF(2) на попарно непараллельные линейные совершенные коды – коды Хэмминга.
Исследованы методы построения транзитивных униформных разбиений пространства Fn на классы смежности двоичных кодов Хэмминга. Разбиение Pn = {H0, H1+e1,…,Hn+en} пространства
Fn на классы смежности двоичных кодов Хэмминга
H0, H1…, Hn длины n называется униформным, если мощность пересечения любых двух различных кодов Хэмминга
Hi, Hj, i,j из {0,1, … , n} есть константа, здесь ei – двоичный вектор длины n веса 1 с единичной i-й координатой.
Для каждого n=2m-1, m>4, построен класс неэквивалентных 2-транзитивных униформных разбиений Fn на классы смежности двоичных кодов Хэмминга. Результат справедлив также для расширенных кодов Хэмминга.
Исследования данного направления относятся к вопросам классификации всех разбиений пространства двоичных
(q-значных) векторов на совершенные коды, что, в свою очередь, напрямую связано с проблемой классификации всех совершенных кодов. Ранее аналогичный результат о разбиениях на максимально непараллельные коды Хэмминга был получен Д. С. Кротовым [Krotov D. S. A partition of the hypercube into maximally nonparallel Hamming codes // Journal of Combinatorial Designs, 22: 4 (2014), 179-187].
[1] Solov'eva F. I. On transitive uniform partitions of Fn into binary Hamming codes, Siberian Electronic Mathematical Reports,
16 (2019), 886-892.
28. Получена полиномиально-временная схема точного решения NP-трудной задачи дискретной оптимизации (PTESS).
С одной стороны, выдвигаемый результат относится к одной частной (хотя и классической) задаче Теории Расписаний.
С другой стороны, он должен представлять интерес (и он действительно интересен коллегам – как показала его презентация на международной конференции в этом году) для гораздо более широкого круга специалистов, выходящего за рамки Теории Расписаний, -- для Дискретной Оптимизации в целом, поскольку представляет собой новый тип результатов и новое направление исследований в этой области.
А именно, при исследовании зависимости сложности исходной (NP-трудной) задачи Теории Расписаний – пропорциональной задачи Open Shop для трёх машин – от некоторого её параметра Г (принимающего на множестве всех примеров задачи значения из интервала [1/3,∞)) впервые построена бесконечная серия полиномиально-разрешимых подзадач, стремящихся сколь угодно близко (по области покрываемых ими примеров) к «почти полной» задаче – за исключением единственного значения параметра Г: Г=1.
При этом для любого e>0 задача с областью определения, исключающей примеры со значением Г из интервала (1-e,1+e), решается с трудоёмкостью
 (где n – число работ во входном примере), т.е. полиномиально разрешима при любом фиксированном
e. По аналогии с давно известными схемами PTAS (polynomial-time approximation scheme), используемыми для приближённого решения NP-трудных задач, полученная нами схема (точного решения подзадач) получила название PTESS (polynomial-time exact solution scheme). (где n – число работ во входном примере), т.е. полиномиально разрешима при любом фиксированном
e. По аналогии с давно известными схемами PTAS (polynomial-time approximation scheme), используемыми для приближённого решения NP-трудных задач, полученная нами схема (точного решения подзадач) получила название PTESS (polynomial-time exact solution scheme).
[1] Sergey Sevastyanov Some positive news on the proportionate open shop problem, Siberian Electronic Mathematical Reports, 16 (2019), 406-426. DOI: 10.33048/semi.2019.16.023
29. Разработаны новые эффективные алгоритмы для построения приближённых решений NP-трудных задач синтеза оптимальных коммуникационных деревьев без дополнительных ограничений и с ограничением на диаметр искомого остовного дерева. Масштабный численный эксперимент на примерах из известной базы показал превосходство предлагаемых алгоритмов над лучшими известными алгоритмами.
В заданном неориентированном реберно-взвешенном графе требуется найти связный остовный подграф, в котором сумма по всем вершинам максимальных весов инцидентных вершине ребер минимальна. Такая задача возникает при минимизации энергозатрат на связь в современных беспроводных сетях, элементы которых способны регулировать дальность передачи. Задача известна в англоязычной литературе как Min-Power Symmetric Connectivity Problem и является NP-трудной в сильном смысле.
В работе предлагается эвристический алгоритм, использующий идеи локального поиска с чередующимися окрестностями и декомпозиции задачи (variable neighborhood decomposition search). Проведен численный эксперимент на псевдослучайно сгенерированных примерах. В результате эксперимента оказалось, что предлагаемый алгоритм решения задачи без ограничений эффективнее наилучших из известных ранее подходов. Также рассмотрена задача с дополнительным ограничением на диаметр искомого подграфа.
Для этой задачи предложен ряд новых конструктивных эвристических алгоритмов и разработаны алгоритмы, использующие идеи таких метаэвристик как: генетический локальный поиск (genetic local search), локальный поиск с чередующимися окрестностями (variable neighborhood search) и алгоритм муравьиной колонии (ant colony optimization). Предлагается постановка задачи в виде задачи целочисленного линейного программирования (ЦЛП).
Для оценки качества разработанных алгоритмов проведен численный эксперимент на псевдослучайно сгенерированных примерах, в ходе которого алгоритмы сравнивались между собой и, в случае малой размерности, с оптимальным решением задачи, полученным с помощью решения ЦЛП пакетом CPLEX. В результате эксперимента определены наиболее эффективные алгоритмы решения задачи для разных вариантов размерности и плотности исходного графа. В случае малой размерности задачи (20-50 вершин), среди предлагаемых конструктивных эвристик всегда находились такие, которые строили решение, отличающееся от оптимального решения (по значению целевой функции) не более чем на 30%, а с помощью предлагаемых метаэвристик почти всегда удавалось получить оптимальное решение задачи. В случае большой размерности, предлагаемые метаэвристики существенно улучшали решения, построенные конструктивными эвристиками: в некоторых случаях удалось почти вдвое уменьшить значение целевой функции.
[1] A. Erzin, R. Plotnikov, N. Mladenovic VNDS for Min-power symmetric connectivity problem, Optimization Letters, 13:8 (2019), 1897-1911. DOI 10.1007/s11590-018-1324-0
[2] R. Plotnikov, A. Erzin Constructive Heuristics for Min-Power Bounded-Hops Symmetric Connectivity Problem, Communications in Computer and Information Science, 1090 (2019), 390-407.
30. Описан общий вид метрических дополнений линейных подпространств булева куба и получена нижняя оценка на мощность наибольших метрически регулярных множеств в булевом кубе.
Метрическим дополнением подмножества A булева куба называется множество векторов, удалённых от данного множества на максимально возможное расстояние (называемое радиусом покрытия A). Если второе метрическое дополнение множества A совпадает с исходным множеством, то множество A называется метрически регулярным.
Задача исследования метрического дополнения множества и метрически регулярных множеств возникает при исследовании бент-функций, множество которых является метрически регулярным, и может быть определено как метрическое дополнение множества аффинных функций. Описан общий вид метрических дополнений линейных подпространств булева куба, найдена оценка на удалённость метрического дополнения произвольного подпространства от самого подпространства. Получено точное описание метрических дополнений подпространств, базис Гаусса-Жордана которых имеет специальный вид. Выделен подкласс строго метрически регулярных множеств, для которого найдены итеративные конструкции порождения его элементов и подсчитано их число. Найдены конструкции двух семейств метрически регулярных множеств большой мощности, что позволило получить наилучшую из известных нижнюю оценку на мощность наибольших метрически регулярных множеств в булевом кубе.
[1] Oblaukhov A. K. Metric complements to subspaces in the Boolean cube, Journal of Applied and Industrial Mathematics,
10:3 (2016), 397-403.
[2] Oblaukhov A. K. Maximal metrically regular sets, Siberian Electronic Mathematical Reports, 15 (2018), 1842-1849.
[3] Oblaukhov A. K. Lower bound on the size of the largest metrically regular subset of the Boolean cube, Cryptography and Communications, 11:4 (2019), 777-791.
31. Найден новый распад «патриарха» тяжёлых мезонов
X(3872), аномально нарушающий изотопическую симметрию за счёт его сложной топологии, треугольной логарифмической сингулярности в амплитуде распада.
Обсуждается нарушающий изотопическую симметрию распад  , обусловленный переходом , обусловленный переходом  , содержащим треугольную логарифмическую сингулярность, , содержащим треугольную логарифмическую сингулярность,
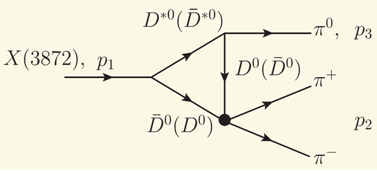
которая доминирует в относительной вероятности распада
 в узкой области в узкой области 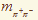 -масс около порога -масс около порога 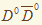 -рождения, 3730-3295 МэВ. Анализ показывает, что можно ожидать относительную величину распада -рождения, 3730-3295 МэВ. Анализ показывает, что можно ожидать относительную величину распада  порядка порядка  . Исследование этого распада на b-фабрике в Японии, c-tau-фабрике в Пекине, Большом Адроном Коллайдере в ЦЕРНЕ, в FERMI Lab в США и на установке PANDA в Германии позволят не только уточнить природу
X(3872)-мезона, но определить длину рассеяния . Исследование этого распада на b-фабрике в Японии, c-tau-фабрике в Пекине, Большом Адроном Коллайдере в ЦЕРНЕ, в FERMI Lab в США и на установке PANDA в Германии позволят не только уточнить природу
X(3872)-мезона, но определить длину рассеяния 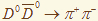 . .
[1] Achasov N. N., Shestakov G. N. Decay  and S-wave and S-wave 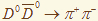 scattering length, Physical Review D, 99:11 (2019), Номер статьи 116023. scattering length, Physical Review D, 99:11 (2019), Номер статьи 116023.
|


