Важнейшие научные результаты Института математики за 2017 год

1. Построены производные объекты, позволяющие классифицировать вполне o-минимальные и слабо o-минимальные теории. Описаны значения и распределения немаксимального числа счетных моделей вполне o-минимальных теорий, из которых вытекает справедливость гипотезы Воота для класса вполне о-минимальных теорий.

1. Пусть T - вполне о-минимальная теория с малым числом счетных моделей. Тогда T имеет ровно 3^k6^s счетных моделей, где k и s являются натуральными числами. Более того, для любых натуральных k, s существует вполне o-минимальная теория T, имеющая ровно 3^k6^s счетных моделей.
2. Пусть T - счетная теория предикатной сигнатуры и с конечным числом неизолированных типов p₁,...,p_n и при этом множество (p₁,...,p_n)-типов конечно. Тогда следующие условия эквивалентны:
(1) теория T почти счетно категорична;
(2) теория T 1-локально счетно категорична.
3. Любая эренфойхтова вполне о-минимальная теория является почти счетно категоричной.
4. Пусть T - счетно категоричная слабо o-минимальная теория. Тогда для любого 1-типа r и натурального числа n алгебра P_ν(r) бинарных изолирующих формул для типа r является (P,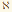₀,n)-wom-моноидом, если и только если RC_bin(r)=n.
5. Пусть T - счетно категоричная слабо о-минимальная теория, p, q – 1-типы. Тогда алгебра P_ν({p,q}) бинарных изолирующих формул для типов p и r является обобщенно коммутативным моноидом, если и только если RC_bin(p)=RC_bin(q).

[1] B. Sh. Kulpeshov, S. V. Sudoplatov Vaught's conjecture for quite o-minimal theories // Annals of Pure and Applied Logic, 2017. Vol. 168, N 1. P. 129-149.
[2] Кулпешов Б. Ш., Судоплатов С. В. Линейно упорядоченные теории, близкие к счетно категоричным // Математические заметки. 2017. Т. 101, № 3. С. 413-424. (английский перевод: Kulpeshov B.Sh., Sudoplatov S.V. Linearly Ordered Theories which are Nearly Countably Categorical // Mathematical Notes, 2017, Vol. 101, No. 3, pp. 94-102.)
[3] Емельянов Д. Ю., Кулпешов Б .Ш., Судоплатов С. В. Алгебры распределений бинарных формул в счетно категоричных слабо о-минимальных структурах // Алгебра и логика. 2017. Т. 56, N 1. С. 20-54. (английский перевод: Emel’yanov D. Yu., Kulpeshov B. Sh., Sudoplatov S. V. Algebras of distributions for binary formulas in countably categorical weakly o-minimal structures // Algebra and Logic, 2017, V. 56, No. 1, pp. 13-36.)

2. Описаны полные решетки с разложениями со свойством замены в определенных классах.

Проблема нахождения характеризации полных решёток, в которых каждый элемент имеет несократимые разложения со свойством замены, восходит к Дилуорсу. Вопрос о существовании подобных разложений в решетках имеет тесную связь с независимой базируемостью аксиоматизируемых классов алгебраических систем с одной стороны и с так называемыми комбинаторными геометриями - с другой.
В работах Дилуорса и Кроули была получена характеризация таких решёток в классе коалгебраических сильно коатомных решёток. Дальнейшие результаты в этом направлении были получены рядом других авторов. В работе Семеновой в 2001 г. были охарактеризованы полные решётки с несократимыми разложениями со свойством замены в классе непрерывных вверх и вниз решёток, а также в классе непрерывных вверх, вполне полудистрибутивных вверх решёток. Мы уточняем этот результат и приводим характеризацию полных решёток с несократимыми разложениями со свойством замены для решёток, обладающих следующими свойствами:
(1) L является либо непрерывной вверх, либо консистентной, либо полумодулярной вверх;
(2) L является либо непрерывной вниз, либо вполне полудистрибутивной вверх.

[1] Швидефски М. В. Разложения в полных решетках. II. Несократимые разложения со свойствами замены // Алгебра и логика, 2017, 56, N 3, 354 -366 (английский перевод Algebra and Logic, 2017, 56, N 3, 236-244)

3. Получены общие достаточные условия для отсутствия простых ∑ - представлений структур в наследственно-конечных надстройках над ∃ - штейницевыми структурами.

Определяется класс ∃ -штейницевых структур, содержащий, в частности, поля вещественных и комплексных чисел. Получены общие достаточные условия для отсутствия простых ∑ -представлений, позволяющие единым методом доказать отсутствие таких представлений в наследственно-конечных надстройках над ∃ -штейницевыми структурами для полугруппы непрерывных функций, некоторых моделей нестандартного анализа, булевой алгебры всех подмножеств ω, симметрической группы множества ω, и многих других.

[1] А. С. Морозов Непредставимость некоторых структур анализа в наследственно конечных надстройках // Алгебра и логика, 2017, Т. 56, No. 6
[2] А. С. Морозов Об одном достаточном условии непредставимости структур в наследственно конечных надстройках
// Алгебра и логика, 2016, Т. 55, No. 3, С. 366–379.
[3] A. S. Morozov Computable model theory over the reals // Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), 2017, No. 10010, P 354-365.

4. Разработаны основы теории нормальных модальных логик с Белнаповскими значениями истинности.

Для суперинтуиционистских логик многие результаты получаются с использование техники нормальных модальных логик. Это возможно благодаря трансляции Геделя-МакКинси-Тарского точно вкладывает интуиционистскую логику в модальную логику S4. Чтобы аналогичным образом исследовать расширения конструктивной логики Нельсона N4 в [1] введена модальная логика BK с Белнаповскими значениями истинности, описана ее семантика Крипке и семантика в терминах твист-структур над модальными алгебрами, построено точное вложение N4 в BS4, аналог логики S4. В [2] доказано, что абстрактное замыкание класса твист-структур над модальными алгебрами задает экивалентую алгебраическую семантику логики BK и найдены инварианты, определяющие строение произвольной твист-структуры. В [3] продолжено изучение алгебраической семантики BK. В [4] описана общая структура класса расширений логики BK, которая аналогична структуре класса расширений логики N4. В [5] проведено сравнение логики BK c аналогичными предложениями других авторов, что завершает первый этап исследования Белнаповских модальных логик.

[1] Odintsov S. P., Wansing H. Modal logics with Belnapian truth values // Journal of Applied Non-Classical Logics, 2010, Vol.20, No.3, P.279-301.
[2] Odintsov S. P., Latkin E. I. BK-lattices. Algebraic Semantics for Belnapian Modal Logics // Studia Logica, 2012, Vol.100,
No.1-2, P.319-338.
[3] Speranski S. O. On Belnapian modal algebras: representations, homomorphisms, congruences, and so on // SEMR, 2013, Vol.10, P. 517-534.
[4] Odintsov S. P., Speranski S. O. The lattice of Belnapian modal loics: Special extensions and counterparts // Logic and Logical Philososphy, 2016, 25, No.1, 3-33.
[5] Odintsov S. P., Wansing H. Disentangling FDE-based Paraconsistent Modal Logics // Studia Logica, 2017, Vol.105, No.6, 1221-1254, DOI: 10.1007/s11225-017-9753-9.

5. Доказано, что существует свободно порождённая проективная плоскость бесконечного ранга любой вычислимой размерности.

Известно, что вычислимая размерность произвольной счётной свободной проективной плоскости может принимать лишь два значения: 1 или ω. При этом вычислимая размерность свободной проективной плоскости равна 1, если и только если ранг проективной плоскости конечен. Возникает естественный вопрос о возможности обобщения данного описания на случай произвольных свободно порождённых проективных плоскостей. В частности, вызывает интерес вопрос о реализуемости в классе свободно порождённых плоскостей вычислимой размерности n, где 1<n<ω.
Изучение вопросов реализуемости вычислимых размерностей связано с проблемами реализуемости различных видов спектров тьюринговых степеней в счётных структурах и является одним из основных направлений исследований в теории вычислимых моделей. Подобные вопросы рассматриваются как в общем случае, так и в конкретных классах алгебраических систем.
Доказано, что класс свободно порождённых проективных плоскостей является полным относительно спектров степеней и эффективных размерностей, т.е. спектры степеней и эффективные размерности, которые удаётся реализовать в каких-либо структурах, можно также реализовать и в классе свободно порождённых плоскостей. Отсюда, как следствие, получен результат о том, что для любого натурального n>0 существует свободно порождённая проективная плоскость бесконечного ранга, вычислимая размерность которой равна n.

[1] Н. Т. Когабаев Свободно порождённые проективные плоскости конечной вычислимой размерности // Алгебра и логика, 55, No.6 (2016), 704-737.
[2] N. Kogabaev. Freely generated projective planes with finite computable dimension // The Bulletin of Symbolic Logic, 23, No.2 (2017), 246-247.

6. Доказано, что любая вычислимая локально конечная структура с конечным числом операций вычислимо изоморфна некоторой структуре, вычислимой за полиномиальное время. Доказано, что любая бесконечная структура, вычислимая за полиномиальное время, не обладает категоричностью.

Структура называется вычислимой за полиномиальное время, если она может быть представлена как множество слов в некотором конечном алфавите, и так, что множество её элементов и все операции и предикаты являются вычислимыми за полиномиальное время (т. е. заданы достаточно эффективными алгоритмами). Структуры вычислима, если указанные объекты заданы некоторыми алгоритмами, без явных ограничений на время их работы.
Доказано, что любая вычислимая локально конечная структура с конечным числом операций вычислимо изоморфна некоторой структуре, вычислимой за полиномиальное время. Доказано, что любая бесконечная структура, вычислимая за полиномиальное время, не обладает категоричностью в том смысле, что существует другая изоморфная ей структура, тоже вычислимая за полиномиальное время, такая что между ними нет вычислимого за полиномиальное время изоморфизма.
Последний результат можно усилить в случае локально конечных структур: доказано, что для любой бесконечной локально конечной структуры, вычислимой за полиномиальное время, существует другая изоморфная ей структура, тоже вычислимая за полиномиальное время такая, что между ними нет даже примитивно рекурсивного изоморфизма.

[1] Алаев П. Е. Структуры, вычислимые за полиномиальное время. I // Алгебра и логика, т.55, № 6 (2016), с.647-669.
[2] Алаев П. Е. Структуры, вычислимые за полиномиальное время. II // Алгебра и логика, т.56, №6 (2017).

7. Доказано, что в классе центральных графов Кэли над почти простыми группами и в классе картановых когерентных конфигураций, ассоциированных с простыми группами лиева типа, проблема изоморфизма решается за полиномиальное время.

Если Г – это граф Кэли над группой G с системой образующих X, то группа Aut(Г) автоморфизмов графа Г содержит регулярную подгруппу, изоморфную группе G. Поэтому при поиске группы Aut(Г) и множества Iso(Г,Г’) всех изоморфизмов из Г в произвольный граф Кэли Г’, мы обладаем некоторой дополнительной заранее известной информацией о Aut(Г). Та же ситуация возникает, когда мы рассматриваем проблему изоморфизма для шуровых когерентных конфигураций Ф=(M,S), где множество базисных отношений S совпадает с 2-орбитами некоторой группы G подстановок множества М, поскольку и в этом случае, G является подгруппой в Aut(Ф). Особый интерес представляет случай, когда G - неабелева простая или почти простая группа. Мы доказываем, что в классе центральных (система образующих X – нормальное множество в G) графов Кэли над почти простыми группами и в классе картановых когерентных конфигураций, ассоциированных с простыми группами лиева типа (здесь группа лиева типа G действует на смежных классах по своей подгруппе Картана), проблема изоморфизма решается за полиномиальное время.

[1] Ponomarenko I., Vasil'ev A. V. Testing isomorphism of central Cayley graphs over almost simple groups in polynomial time
// Записки научн. сем. ПОМИ, 2017, Т. 455, 154-180.
[2] Ponomarenko I., Vasil'ev A. V. Cartan coherent configurations // J. Algebra Comb., 2017, Vol. 45, N 2, 525-552.

8. Доказана локальная конечность периодической группы, в которой любая конечная подгруппа содержится в подгруппе, изоморфной простой симплектической группе размерности 4 над полем чётного порядка.

Пусть M – некоторое множество групп. По определению, группа G насыщена группами из M, если любая конечная подгруппа из G содержится в подгруппе, изоморфной некоторому элементу M. Известная гипотеза состоит в том, что периодическая группа локально конечна, если она насыщена конечными простыми группами лиева типа ограниченного лиева ранга. К настоящему времени эта гипотеза подтверждена для случая, когда насыщащающее множество состоит из конечных простых групп лиева ранга 1 и некоторых групп лиева ранга 2. Авторы подтверждают эту гипотезу для случая, когда насыщающее множество состоит из простых симплектических групп размерности 4 над конечными полями чётных порядков.

[1] Д. В. Лыткина, В. Д. Мазуров Характеризация простых симплектических групп размерности 4 над локально конечными полями характеристики 2 в классе периодических групп // Сибирск. матем. журнал, 58, № 5 (2017), 1098-1109.
DOI: 10.17377/smzh.2017.58.512.

9. Для несимметрических q-квазиметрических квазиметрик доказаны теоремы об их билипшицевой эквивалентности квазиметрикам и теорема об их регуляризации, обобщающая известный результат Р. Машиас и К. Сеговиа. Для достаточно широкого класса несимметрических q-квазиметрических пространств установлена их топологическая регулярность.

(q₁, q₂)-квазиметрикой называется неотрицательная функция ρ, определенная на декартовом произведении X×X, где X− некоторое множество, состоящее не менее чем из двух элементов, такая, что для нее выполняются следующие аксиомы: ρ(x,y)=0 тогда и только тогда, когда x=y; ρ(x,z)≤q₁ρ(x,y)+q₂ρ(y,z) для всех x,y,z из X, где q₁,q₂- некоторые положительные константы. (q₁, q₂)-квазиметрические пространства были введены в 2014 г. А. В. Арутюновым и
А. В. Грешновым в связи с развитием теории неподвижных точек однозначных и многозначных отображений. Примерами (q₁, q₂)-квазиметрик являются Box-квазиметрики эквирегулярных пространств Карно−Каратеодори, а также квазиметрики пространств L_p, где 0<p<1.
Доказано, что условия (q₁, 1)- и (1, q₂)-квазиметричности функции расстояния являются достаточными для существования 1-квазиметрики, билипшицево ей эквивалентной. Откуда следует, что Box-квазиметрика, определяемая при помощи базисных векторных полей класса C¹, коммутаторы которых самое большее складывают их степени, билипшицево эквивалентна некоторой метрике. Вместе с тем установлено, что необходимыми эти условия не являются. Доказано существование (q₁, q₂)-квазиметрик, для которых не существует 1-квазиметрик, липшицево им эквивалентных, откуда, в частности, вытекает другое доказательство известного результата В. Шредера. Доказано, что для произвольной (q₁, q₂)-квазиметрики ρ, определенной на некотором множестве X, всегда найдется билипшицево эквивалентная ей (p₁, p₂)-квазиметрика d такая, что для любой точки y из X и для любого r>0 множество, состоящее из тех x из X, что d(y,x)<r, является открытым в топологии «открытых шаров» (q₁, q₂)-квазиметрического пространства (X, ρ) (теорема о регуляризации (q₁, q₂)-квазиметрики). Ранее подобная теорема была известна только на квазиметрических пространствах с обобщенной симметрией. Введено понятие lim-слабо симметрических (q₁, q₂)-квазиметрических пространств, построены примеры lim-слабо симметрических (q₁, q₂)-квазиметрических пространств, не являющихся слабо симметрическими, доказано выполнение аксиомы отделимости T₃ для lim-слабо симметрических (q₁, q₂)-квазиметрических пространств.

[1] Грешнов А. В. (q₁, q₂)- Квазиметрики, билипшицево эквивалентные 1-квазиметрикам // Матем. тр., 20:1 (2017), 81–96.
[2] Грешнов А. В. Регуляризация функций расстояния и аксиомы отделимости на (q₁, q₂)-квазиметрических пространствах // Сиб. электрон. матем. изв., 14 (2017), 765–773.

10. Установлена формула площади для классов гёльдеровых отображений групп Карно.

На нильпотентных градуированных группах (и, в частности, группах Карно) исследованы классы отображений, являющихся гёльдеровыми относительно субримановых (квази)метрик. А именно, рассмотрены гладкие в римановом смысле отображения, а также их графики и графики липшицевых в субримановом смысле отображений. Для вывода метрических свойств использовано новое понятие полиномиальной субримановой дифференцируемости, суть которого состоит в аппроксимации отображением, аналогичным не линейному отображению, а полиному. Отметим, что точность приближения координатных функций такими полиномами зависит от степени соответствующего им поля. Следующим инструментом исследования является понятие внутреннего, или адаптированного, базиса, позволяющее согласовать две субримановы структуры: образа отображения и пространства-образа. Установлено, что перечисленные классы отображений являются полиномиально субриманово дифференцируемыми, и что для них в окрестности каждой точки существует адаптированный базис. Эти результаты составили основу для доказательства формулы площади, которая характеризует внутреннюю (субриманову) меру поверхности-образа. В частности, показано, что для отображений-графиков вид формулы площади аналогичен классическому.

[1] Карманова М. Б. О полиномиальной субримановой дифференцируемости некоторых гёльдеровых отображений групп Карно // Сибирский математический журнал, 2017. Т. 58, № 2, С.305-332.
[2] Карманова М. Б. Формулы площади для классов гёльдеровых отображений групп Карно // Сибирский математический журнал, 2017. Т. 58, № 5. С. 1056-1079.
[3] Карманова М. Б. Гёльдеровы отображения групп Карно и внутренние базисы // Доклады Академии наук, 2017. Т. 472, № 1. С. 7-10.
[4] Карманова М. Б. Метрические свойства классов гёльдеровых поверхностей на группах Карно // Доклады Академии наук, 2017. Т. 473, № 1. С. 17-20.

11. Дано исчерпывающее описание граничных значений конформных отображений плоских конечносвязных областей в терминах конформных модулей (экстремальных длин) пар граничных компонент рассматриваемой области в том случае, когда связность ее меньше либо равна 3.

Ранее рассматривалась и успешно решалась задача об однозначной определенности пространственных областей относительными конформными модулями их граничных конденсаторов. В работе [1] эта задача решается в случае плоских n-связных областей при n ≤ 3. Основной ее результат - утверждение о том, что всякая n-связная плоская область U при n ≤ 3 однозначно определяется относительными конформными модулями пар граничных компонент. Главные трудности в решении обсуждаемой задачи обнаруживаются при n ≤ 3 и начинаются в случае n = 3. При этом на первый план выдвигается поиск подходящих теорем о конформных отображениях многосвязных областей на области канонических видов (круговые, спиралевидные и др.).

[1] Копылов А. П. Об однозначной определенности трехсвязных плоских областей относительными плоскими конформными модулями пар граничных компонент // Сибирский журнал чистой и прикладной математики, 17:2 (2017), стр.13-20.

12. Разработаны основы теории нелинейных параметрических возмущений абстрактных гиперболических систем.

В банаховом пространстве рассмотрены дифференциальные уравнения
с замкнутыми попарно коммутативными линейными операторами A_j, порождающими равномерно ограниченные и сильно непрерывные группы 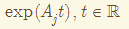; ε - малый скалярный параметр, нелинейное возмущение F(t,u) почти периодично по t. Такие уравнения являются абстрактными аналогами гиперболических систем. Подобную интерпретацию допускают уравнения Шрёдингера, системы уравнений акустики, волновые уравнения и многие другие.
Для класса систем порядка m=2 с операторами A_j, имеющими точечный спектр, найдены условия параметрического резонанса, т.е. потери устойчивости при ε ≠ 0 . Преодолена возникающая при этом проблема малых знаменателей и построена эффективная асимптотика решений, когда ε → 0. Для класса систем порядка m=1 с оператором A₁, спектр которого абсолютно непрерывен, наоборот, установлены достаточные условия устойчивости возмущенных уравнений.

[1] В. С. Белоносов Спектральные свойства обобщенных функций и асимптотические методы теории возмущений
// Матем. сб., 203:3 (2012), 3–22.
[2] В. В. Сказка О влиянии непрерывного спектра на эффект параметрического резонанса. Случай ограниченных операторов // Матем. сб., 205:5 (2014), 77–96.
[3] В. С. Белоносов Асимптотический анализ параметрической неустойчивости нелинейных гиперболических уравнений
// Матем. сб., 208:8 (2017), 4–30.
[4] В. В. Сказка Об устойчивых возмущениях линейных дифференциальных уравнений, порождающих равномерно ограниченную группу // Матем. сб., 208:8 (2017), 168–182.

13. Доказано, что на двумерном торе существуют метрики, отличные от лиувиллевых, магнитный геодезический поток которых на фиксированном уровне энергии обладает квадратичным по импульсам первым интегралом.

В работах М. Бялого и А. Е. Миронова было показано, что наличие у магнитного геодезического потока на двумерном торе на фиксированном уровне энергии полиномиального по импульсам первого интеграла, независимого от интеграла энергии, эквивалентно существованию гладких периодических решений соответствующей полугамильтоновой системы дифференциальных уравнений в частных производных на метрику и коэффициенты первого интеграла. В настоящей работе доказано существование глобальных решений у этой системы в случае интеграла второй степени. А именно, доказано, что на двумерном торе существуют метрики, сколь угодно близкие к лиувиллевым (и в то же время отличные от них), геодезический поток которых в слабом магнитном поле на фиксированном уровне энергии обладает квадратичным по импульсам первым интегралом.

[1] Agapov S. V., Bialy M., Mironov A. Е. Integrable magnetic geodesic flows on 2-torus: new examples via quasi-linear system of PDEs // Communications in mathematical physics, 2017. Vol. 351. \No 3, P. 993-1007.

14. Получены условия экспоненциальной устойчивости решений некоторых классов систем нейтрального типа с периодическими коэффициентами и установлены оценки скорости стабилизации решений на бесконечности.

Рассмотрены системы дифференциальных уравнений с запаздывающим аргументом, относящиеся к системам нейтрального типа, когда все матрицы коэффициентов являются периодическими. Получены достаточные условия экспоненциальной устойчивости решений и установлены оценки решений, характеризующие скорость убывания решений на бесконечности. Условия устойчивости формулируются в терминах дифференциальных матричных неравенств. Результаты распространены на системы с несколькими запаздываниями. При получении результатов использовались новые функционалы типа Ляпунова-Красовского.

[1] Матвеева И. И. Об экспоненциальной устойчивости решений периодических систем нейтрального типа // Сибирский математический журнал. 2017. Т. 58, № 2. С. 344-352.
[2] Матвеева И. И. Об экспоненциальной устойчивости решений периодических систем нейтрального типа с несколькими запаздываниями // Дифференциальные уравнения. 2017. Т. 53, № 6. С. 730-740.

15. Впервые установлен расширенный принцип больших уклонений для траектори случайного процесса с независимыми приращениями при выполнении слабого моментного условия Крамера.

Исследование вероятностей больших уклонений для различных схем случайных блужданий и случайных процессов с непрерывным временем играет важную роль в ряде прикладных задач, где требуется оценить вероятности редких событий. В представляемой работе установлен так называемый расширенный принцип больших уклонений для траекторий случайных процессов с независимыми приращениями при выполнении слабого моментного условия Крамера.
При получении этого результата существенную роль играет аналогичный результат для траекторий обобщенного пуассоновского процесса, впервые полученный автором в 2016 г. В данной работе в полной мере используется новый подход в задаче описания вероятностей больших уклонений для траекторий случайных процессов, предложенный недавно А. А. Боровковым и А. А. Могульским.

[1] Могульский А. А. Расширенный принцип больших уклонений для процесса с независимыми приращениями. Сибирский матем. журнал, 2017, т.58, № 3, с. 660-672.

16. Описаны асимптотические свойства первого и второго порядка для матриц восстановления и моментов для критических ветвящихся процессов Беллмана-Харриса с несколькими типами частиц, имеющими бесконечные средние продолжительности жизни и, возможно, несоизмеримые хвосты для продолжительности жизни у разных частиц.

Критические процессы Беллмана-Харриса с несколькими типами частиц и, возможно, бесконечными средними временами их жизни, где самый тяжелый хвост распределения q(t) правильно меняется с показателем –β [-1,0), были описаны в терминах этого самого тяжелого хвоста. Подходов к описанию свойств частиц с бесконечно малыми хвостами времени жизни относительно q(t) не было. Асимптотические результаты для приращений первого и второго порядков матрицы восстановления, индуцированной ветвящимися процессами, открывают возможности для точного описания свойств коротко живущих типов частиц. Для численности частиц любого типа описаны главные члены для первых и вторых моментов и приращений у первых моментов.

[1] Топчий В. А. О связанных с ветвящимися процессами матрицах восстановления с различным порядком убывания хвостов распределений // Математические труды, 2017, том 20, №2, c.139-192.
[2] В. А. Ватутин, В. А. Топчий Асимптотика вероятностей наличия частиц разных типов с различной скоростью убывания хвостов их продолжительности жизни в многомерных критических процессах Беллмана–Харриса. // Сиб. электр. мат. известия, 2017, No. 14.

17. Доказано существование устойчивой периодической траектории нелинейно динамической системы, моделирующей кольцевую генную сеть.

Изучена геометрия фазовых портретов нелинейных динамических систем, моделирующих функционирование генных сетей, регулируемых только отрицательными обратными связями (молекулярных репрессиляторов). Для этих систем описаны все особые точки, установлены условия существования циклов, построены ретрагирующиеся на эти циклы их инвариантные окрестности, установлены условия устойчивости таких циклов, описаны комбинаторные структуры их фазовых портретов. Аналогичные результаты были получены и для ряда генных сетей с переменными обратными связями; для них были также построены инвариантные поверхности, содержащие эти циклы.
Полученные результаты применяются к моделированию природных генных сетей и согласуются с данными биологических экспериментов.

[1] Голубятников В. П., Казанцев М. В. Об одной кусочно-линейной динамической системе, моделирующей генную сеть с переменной обратной связью // Сибирский журнал чистой и прикладной математики. 2016, т.16, N 4, с. 28 – 37.
[2] Аюпова Н. Б., Голубятников В. П. Трёхклеточная модель ранней стадии развития одного пронейрального кластера
// Сибирский журнал индустриальной математики. 2017, т. 20, N 2, с. 15 – 20.
[3] Аюпова Н. Б., Голубятников В. П., Казанцев М. В. О существовании цикла в одной несимметричной модели молекулярного репрессилятора // Сибирский журнал вычислительной математики. 2017, т. 20, N 2, с. 121 – 129.
[4] Голубятников В. П. Вопросы существования устойчивого цикла в одной модели молекулярного репрессилятора
// Математические структуры и моделирование. 2017, N 2 (42), с. 59 – 67.

18. Установлен аналог известной теоремы Бондаревой–Шепли о ядре для случая нечетких кооперативных игр, когда возможности блокирования расширяются за счет нечетких коалиций.

Получен аналог известной теоремы Бондаревой–Шепли для нечетких кооперативных игр, когда возможности блокирования расширяются за счет так называемых нечетких коалиций. Основу предлагаемого подхода составляет распространение классического понятия сбалансированного семейства на случай нечетких коалиций, что позволяет ввести естественное обобщение сбалансированности для рассматриваемых нечетких игр. Установлено, что указанная обобщенная сбалансированность является необходимым и достаточным условием непустоты ядра нечеткой кооперативной игры. Приводятся уточнения критерия непустоты ядра, основанные на использовании классической теоремы Хелли о пересечении выпуклых множеств. Изучается так называемое S∗-представление нечеткой игры, облегчающее в ряде случаев анализ условий существования неблокируемых дележей этой игры.

[1] В. А. Васильев. Аналог теоремы Бондаревой–Шепли I. Непустота ядра нечеткой игры // Математическая теория игр и её приложения. 2017. Том 9, вып. 1, с. 3-26.
[2] V. A. Vasil’ev A fuzzy-core extension of Scarf theorem and related topics // Contributions to game theory and management. Vol. 8. SPb.: Graduate School of Management SPbU, 2015, p. 300-314.

19. Доказана теорема существования и единственности олигополистических равновесий в экономике с аддитивно-сепарабельными предпочтениями общего вида. Проведён сравнительный анализ равновесий для трёх типов несовершенной конкуренции в терминах цен, ассортимента выпуска и функции общественного благосоcтояния.

Проведен сравнительный анализ равновесий в отрасли в условиях монополистической конкуренции и олигополий Курно и Бертрана со свободным входом фирм. Потребительский сектор характеризуется аддитивно-сепарабельными предпочтениями. Показано, что в условиях монополистической конкуренции фирмы устанавливают цены ниже, чем олигополии, в то же время спектр разнообразия товаров выше при олигополистической конкуренции. Если же размер экономики неограниченно растет, то цены для всех типов конкуренции асимптотически сходятся к одной и той же величине, которая совпадает с совершенно конкурентной ценой только лишь при определенных условиях на потребительские предпочтения.

[1] Parenti M., Sidorov A. V., Thisse J.-F., Zhelobodko E. Cournot, Bertrand or Chamberlin: Toward a Reconciliation
// International Journal of Economic Theory, 2017, V.13, Issue 1, p. 29-45.

20. Методом приближенного обращения решены задачи векторной и 2-тензорной томографии. Построены и программно реализованы алгоритмы решений.

С целью решения задач векторной и 2-тензорной томографии модифицирован и обоснован метод приближенного обращения, развиваемый более 30-ти лет А. К. Луисом (Германия) и его учениками. Теоретические основы метода лежат в функциональном анализе. Это теорема Рисса о представлении линейного функционала, понятие фундаментального решения и его свойства, приближение δ-функции. Метод прекрасно себя зарекомендовал при решении задач обращения линейных и нелинейных операторных уравнений, в частности в скалярной томографии.
Разработаны два алгоритма численного решения указанных задач, исходными данными для которых являются те или иные лучевые преобразования. Первый алгоритм позволяет восстанавливать компоненты векторного или симметричного 2-тензорного поля, в то время как второй позволяет восстановить потенциалы соленоидального и потенциальных частей полей Алгоритмы численно реализованы, приведены результаты вычислительных экспериментов.

[1] Derevtsov E. Yu., Louis A. K., Maltseva S. V., Polyakova A. P., Svetov I. E. Numerical solvers based on the method of approximate inverse for 2D vector and 2-tensor tomography problems // Inverse problems, 2017, vol.33, No 12, art. no. 124001. Special issue on 100 years of the Radon transform.

21. Построен новый генетический алгоритм для задачи календарного планирования с ограниченными ресурсами, показавший рекордные результаты на примерах из библиотеки PSPLIB.

Опубликован цикл работ, посвященных задаче календарного планирования с ограниченными ресурсами по критерию минимизации длины расписания (RCPSP). Она является классической задачей в области исследования операций, и имеет обширные приложения в различных областях. В задаче учитываются технологические ограничения предшествования работ, а также ресурсные ограничения. Все ресурсы являются возобновимыми. Эта задача принадлежит к классу NP-трудных задач. Были разработаны несколько алгоритмов решения RCPSP. Предложены быстрые жадный и стохастический жадный алгоритмы, среди жадных алгоритмов предложенный алгоритм занимает одни из лучших позиций, а на тестовых примерах J60 из PSPLIB по 50000 испытаний он показал лучший результат. Предложен также генетический алгоритм, в кроссовере которого применяется эвристика, учитывающая степень критичности ресурсов, которая выявляется из решения релаксированной задачи с ограничением на ресурсы складируемого типа. Был проведен численный эксперимент на примерах из библиотеки PSPLIB. Для девяти примеров из тестовой серии j120 были найдены лучшие решения, а для j60 (50000 и 500000 итераций) и для j120 (500000 итераций) получены лучшие средние отклонения решений от величины критического пути.

[1] Гончаров Е. Н., Леонов В. В. Генетический алгоритм для задачи календарного планирования с ограниченными ресурсами // Автомат. и телемех., 2017, № 6, c.173-189. (Перевод: Goncharov E.N., Leonov V.V. Genetic Algorithm for the Resource-Constrained Project Scheduling Problem // Automation and Remote Control, 2017, Vol. 78, № 6, pp. 1101–1114).
[2] Е. Н. Гончаров Стохастический жадный алгоритм для задачи календарного планирования с ограниченными ресурсами
// Дискретный анализ и исследование операций, Новосибирск: Изд-во ИМ СО РАН, 2014, Том 21, № 3, с. 10-23.
[3] Goncharov E. N. A greedy heuristic approach for the resource-constrained project scheduling problem // Studia Informatica Univeralis, 2012, vol. 9, N. 3, p. 79–90.

22. Доказано, что для любой стандартной нормы ℓ_p задача поиска подмножества векторов с наибольшей нормой суммы имеет порог неприближаемости в классе полиномиальных алгоритмов (если P≠NP). Для случая произвольного нормированного пространства предложен алгоритм точного решения задачи с трудоёмкостью, меньшей трудоёмкости известных алгоритмов, и полиномиальной при фиксированной размерности пространства.

Выдвигается ряд работ, посвященных следующей оптимизационной задаче. Для заданного конечного множества векторов в нормированном векторном пространстве найти подмножество, на котором достигается максимальное значение нормы суммарного вектора. Доказано, что для любой стандартной нормы ℓ_p, где 1≤p<∞, задача имеет порог неприближаемости в классе полиномиальных алгоритмов, если P≠NP. С другой стороны, для случая произвольного нормированного пространства предложен алгоритм точного решения задачи с трудоёмкостью, меньшей трудоёмкости известных алгоритмов, и полиномиальной при фиксированной размерности пространства. В частности, если векторы входного множества расположены на плоскости, задача разрешима за почти линейное время. Предложены алгоритмы, имеющие рекордную трудоёмкость, для модификаций задачи, в которых задана мощность искомого подмножества либо эта мощность влияет на значение целевой функции.

[1] Shenmaier V. V. and Algorithms for Finding a Subset of Vectors with the Longest Sum // In: Cao, Y., Chen, J. (eds.) COCOON 2017. LNCS, vol. 10392, pp. 469–480, Springer, Cham (2017).
[2] Шенмайер В. В. Точный алгоритм для нахождения подмножества векторов с суммой максимальной длины // Дискрет. анализ и исслед. операций. 2017. Т. 24, № 4. С. 111-129.
[3] Шенмайер В. В. Решение некоторых задач поиска подмножества векторов с использованием диаграмм Вороного
// Дискрет. анализ и исслед. операций. 2016. Т. 23, № 4. С. 102–115. (Перевод: Shenmaier V.V., Solving some vector subset problems by Voronoi diagrams // J. of Applied and Industrial Mathematics, 2016, Vol. 10, № 4, P.560–566.)

23. Предложен метод описания префикс-реверсальных кодов Грея, а также найдено необходимое условие существования жадных кодов Грея.

Префикс-реверсальным кодом Грея называется способ порождения перестановок на n элементах, где каждая последующая отличается от предыдущей инверсией префикса (начального сегмента перестановки), и является обобщением классического кода Грея, введенного в 1958 году. Понятие префикс-реверсального кода Грея было введено А. Вильямсом в 2013 году вместе с предложенной им, так называемой, конструкцией жадного кода Грея, где был поставлен вопрос о существовании других кодов Грея в рамках этой конструкции. Помимо конструкции Вильямса была известна только конструкция, полученная С. Заксом в 1984 году. Префикс-реверсальные коды Грея имеют прямое соответствие гамильтоновым циклам в Pancake графе, являющимся графом Кэли на симметрической группе с порождающим множеством префикс-реверсалов.
Предложен метод описания префикс-реверсальных кодов Грея, обобщающий известные конструкции Вильямса и Закса, который основывается на покрытии Pancake графа максимальным множеством независимых циклов. В рамках данного подхода получено необходимое условие существования жадных кодов Грея, а также описаны случаи несуществования префикс-реверсальных кодов Грея.

[1] E. V. Konstantinova, A. N. Medvedev Independent even cycles in the Pancake graph and greedy Prefix-reversal Gray codes
// Graphs and Combinatorics, 32 (2016) 1965-1978.
[2] E. V. Konstantinova Chromatic properties of the Pancake graphs // Discussiones Mathematicae Graph Theory, 37 (2017)
777–787.

24. Получена характеризация классов Z₄-линейных расширенных 1-совершенных кодов и Z₄-линейных кодов Адамара, описаны группы автоморфизмов этих кодов.

Z₄-линейными называются двоичные коды, полученные при помощи отображения Грея f: f(0)=00, f(1)=01, f(2)=11, f(3)=10 из линейных кодов над кольцом Z/4Z. Более общее понятие, Z₂Z₄-линейный код, обозначает двоичный код, полученный аналогичным образом из аддитивного кода в смешанном алфавите: часть координат изначально двоичная, а часть четверичная. Двоичные коды с параметрами (длина, мощность, кодовое расстояние), равными (n,2ⁿ/2n,4), называются расширенными 1-совершенными, а коды с параметрами (n,2n,n/2) - кодами Адамара. Построен класс Z₄-линейных расширенных 1-совершенных кодов, получена характеризация всех таких кодов, с точностью до эквивалентности; их число оказалось растущим, порядка log n. Аналогичный результат получен для класса Z₄-линейных кодов Адамара; позже (совместно с М. Виллануевой) завершена классификация всех неэквивалентных Z₂Z₄-линейных кодов Адамара. Описаны группы автоморфизмов Z₂Z₄-линейных расширенных 1-совершенных кодов и Z₂Z₄-линейных кодов Адамара. При этом оказалось, что все автоморфизмы Z₂Z₄-линейных расширенных 1-совершенных кодов сохраняют Z₂Z₄-структуру кода (другими словами, не разбивают пары координат, соответствующие одной Z₄-координате), за исключением кодов длины 16 и меньше. Для Z₂Z₄-линейных кодов Адамара это не так, группа автоморфизмов двоичного кода оказалась в общем случае больше, чем группа автоморфизмов соответствующего ему аддитивного кода в смешанном Z₂-Z₄ алфавите.

[1] D. S. Krotov On the automorphism groups of the Z₂Z₄-linear 1-perfect and Preparata-like codes // Designs, Codes and Cryptography, 2017, Vol. 83, Iss. 1, P. 169-177.
[2] D. S. Krotov, M. Villanueva Classification of the Z₂Z₄-linear Hadamard codes and their automorphism groups // IEEE Transactions on Information Theory, 20015, Vol. 61, Iss.2, P. 887-894.
[3] D. S. Krotov Z₄-Linear Hadamard and extended perfect codes // Electronic Notes in Discrete Mathematics, 2001,Vol. 6,
P. 107-112.
[4] Д. С. Кротов Z₄-линейные совершенные коды // Дискретн. анализ и исслед. операций, Сер. 1, 2000, Том 7, №.4,
С. 78-90.

25. Доказано, что число 1-факторов в любом d-униформном гиперграфе можно ограничить сверху с помощью перманента его матрицы смежности. Также в качестве следствия получена верхняя оценка на число 1-факторизаций полного гиперграфа.

Гиперграф H на n вершинах называется d-униформным, если каждое его гиперребро состоит из d вершин. 1-фактор в гиперграфе H – это такой набор его гиперребер, который покрывает каждую вершину ровно один раз, а 1-факторизация – это разбиение всех гиперребер гиперграфа на непересекающиеся 1-факторы. Матрицей смежности M(H) гиперграфа H назовем такую d-мерную (0,1)-матрицу порядка n, что ее элемент с индексом α=(α₁,...,α_d) равен единице тогда и только тогда, когда α есть гиперребро гиперграфа H.
Доказано, что для любого d≥4 существует такая константа 0 < μ(d) < 1 , что количество 1-факторов в любом d-униформном гиперграфе H на n вершинах не превосходит (μ(d)ⁿperM(H))^1/d . Этот результат является обобщением аналогичного утверждения для графов. Ранее было известно, что число совершенных паросочетаний в любом графе не больше, чем квадратный корень из перманента его матрицы смежности [N. Alon, S. Friedland, The maximum number of perfect matchings in graphs with a given degree sequence // Electron. J. Combin. (2008) 15].
Следствием полученного результата является первая нетривиальная асимптотическая верхняя оценка числа 1-факторизаций полного d-униформного гиперграфа на вершинах.
3-униформный гиперграф на 6 вершинах с 4 гиперребрами, содержащий два 1-фактора (синий и красный), объединение которых является 1-факторизацией гиперграфа.

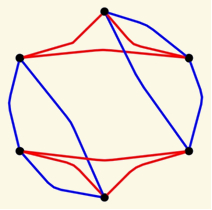
[1] A. A. Taranenko On the numbers of 1-factors and 1-factorizations of hypergraphs // Discrete Mathematics, 2017, Vol. 30,
P 753-762. DOI: 10.1016/j.disc.2016.11.024.

26. Получено асимптотически точное приближение числа n-вершинных помеченных графов в классах графов (как связных, так и не обязательно связных), содержащих кратчайшую цепь длины не менее заданной, и графов фиксированного диаметра. Описаны векторы разнообразия шаров и установлен ряд свойств для почти всех графов заданного диаметра.

Исследованы в асимптотике строение и число n-вершинных графов, содержащих кратчайшую цепь заданной длины. Известно, что почти все графы имеют диаметр 2. Доказано, что при фиксированном k≥3 асимптотически равномощны следующие классы помеченных n-вершинных графов: графы диаметра k, связные графы диаметра не менее k и графы (не обязательно связные), имеющие кратчайшую цепь длины не менее k. Получено асимптотически точное приближение числа таких n-вершинных графов, и найдена явная оценка погрешности при этом приближении. В частности, улучшены оценки для ранее полученного З. Фюреди и Ю. Кимом асимптотического приближения числа n-вершинных графов фиксированного диаметра k. Установлено, что почти все графы диаметра k имеют единственную пару диаметральных вершин, но почти все графы диаметра 2 имеют более одной пары таких вершин. Получено решение проблемы описания векторов разнообразия шаров (i-я компонента вектора равна числу различных шаров радиуса i) для почти всех графов заданного диаметра.

[1] Т. И. Федоряева Асимптотическое приближение числа n-вершинных графов заданного диаметра // Дискретный анализ и исследование операций, 2017, т.24, № 2, С.68-86. DOI: 10.17377/daio.2017.24.534
[2] T. I. Fedoryaeva Asymptotic approximation for the number of n-vertex graphs of given diameter // Journal of Applied and Industrial Mathematics, 2017, v.11, № 2, pp.204-214. DOI: 10.1134/S1990478917020065
[3] Т. И. Федоряева Строение вектора разнообразия шаров типичного графа заданного диаметра // Сибирские электронные математические известия. 2016. Т.13. С. 375-387. DOI: 10.17377/semi.2016.13.033 WOS:000407781100033

27. Получены различные конструкции нелинейных совершенных двоичных кодов бесконечной длины.

Подмножество C в бесконечномерном двоичном кубе называется совершенным двоичным кодом c расстоянием 3, если все шары единичного радиуса (в метрике Хэмминга) с центрами из C попарно не пересекаются и их объединение покрывает двоичный куб. Аналогичным образом определяется совершенный код в нулевом слое, т. е. на множестве всех векторов, имеющих конечные нормы Хэмминга. В работе доказывается, что мощность множества всех классов эквивалентности совершенных двоичных кодов в нулевом слое бесконечномерного двоичного куба равна континууму, а мощность множества классов эквивалентности совершенных двоичных кодов во всём кубе равна гиперконтинууму. Говорят, что совершенный код C имеет полную систему троек, если множество C + C содержит все векторы двоичного куба веса 3. Такие коды являются несистематическими. В конечномерном случае они были впервые построены С. В. Августиновичем и Ф. И. Соловьевой в 1996 г. с помощью свитчингов определенного набора компонент, находящихся на достаточно большом расстоянии друг от друга. Оказалось, что для кодов бесконечной длины аналогичное требование “разреженности” компонент является необходимым. В работе предлагается конструкция несистематических кодов бесконечной длины, имеющих полную систему троек.

[1] Малюгин С. А. Совершенные двоичные коды бесконечной длины // Дискретный анализ и исследование операций, 2017, т. 24, № 2, С.53-67.
[2] Малюгин С. А. Совершенные двоичные коды бесконечной длины с полной системой троек // Сибирские электронные математические известия. 2017. Т.14. С. 877-888.

28. Получены и подробно рассмотрены новые распады тяжёлых мезонов, в которых можно исследовать аномальное нарушение изотопической инвариантности на c-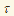-фабрике в Пекине и на супер-b-фабрике в Японии.

Теоретически открытое в 1979 году в Институте математики СО АН СССР аномальное нарушение изотопической симметрии при рождении лёгких скалярных мезонов в настоящее время открыто экспериментально и интенсивно исследуется. Исследование этих эффектов позволяет изучать как природу лёгких скалярных мезонов, так и динамические механизмы их рождения. Подробно рассмотрены три новы распада тяжёлых мезонов, в которых можно исследовать аномальное нарушение изотопической инвариантности на c--фабрике в Пекине и на супер-b-фабрике в Японии.

[1] N. N. Achasov, G. N. Shestakov Strong isospin breaking at production of light scalars // NUCLEAR AND PARTICLE PHYSICS PROCEEDINGS, 287–288, 89-94 (2017).
[2] N. N. Achasov, G. N. Shestakov Manifestations of the a00(980)−f0(980) mixing in D0→K0Sπ+π− and D0→K0Sηπ0 decays
// PHYSICAL REVIEW D 96, 016027 (2017).
[3] N. N. Achasov, G. N. Shestakov Interference phenomena in the decay D+s→ηπ0π+ induced by the a00(980)−f0(980) mixing // PHYSICAL REVIEW D 96, 036013 (2017).
[4] N. N. Achasov and G. N. Shestakov Observationof the isospin breaking decay $Y(10860) \to Y(1S)f_0(980)\to Y (1S)\eta\pi^0$ with the Belle II detector // PHYSICAL REVIEW D 96, 091501(R) (2017). DOI: 10.1103/PhisRefD.96.091501