Важнейшие научные результаты Института математики за 2016 год

1. Описаны простые йордановы супералгебры с ассоциативной полупростой четной частью.

Класс йордановых алгебр, возникших в задачах квантовой механики в 1930-х годах, отличается тем, что в нем имеется исчерпывающая классификация простых объектов (Е.И. Зельманов, 1984). В то же время, структурная теория бесконечномерных йордановых супералгебр далека от завершения. В данной работе исследуются простые йордановы супералгебры с ассоциативной ниль-полупростой четной частью, у которых два четных элемента индуцируют ненулевое дифференцирование. Доказано, что такую супералгебру можно получить из простой абелевой йордановой супералгебры, четная часть которой является дифференциально простой ассоциативной коммутативной алгеброй, а нечетная часть - конечно-порожденным проективным модулем ранга 1. Кроме того, эти супералгебры являются порядками простых супералгебр йордановых скобок.

[1] В. Н. Желябин Простые йордановы супералгебры с ассоциативной ниль-полупростой четной частью. // Сиб. мат. журнал, 2016, том 57, № 6, С. 1262-1279.

2. Описаны произвольные 2-группы, в которых любая конечная подгруппа порождается двумя элементами. Доказано, в частности, что они локально конечны.

С. И. Адян доказал, что в не локально конечных бернсайдовых группах нечетного периода любая конечная подгруппа циклическая. В 2-группах ситуация иная: например, известно, что любая неабелева 2-группа содержит конечную неабелеву подгруппу, а 2-группа, в которой любая конечная подгруппа двуступенно нильпотентна, сама двуступенно нильпотентна и, следовательно, локально конечна. Эти обстоятельства оправдывают исследования, направленные на доказательство локальной конечности 2-групп с заданными свойствами их конечных подгрупп. Первый из представленных результатов переносит на произвольные 2-группы известную классификацию2-групп, содержащих совпадающую со своим централизатором подгруппу порядка 4. Как следствие показывается, что такие группы локально конечны. На основе этого результата доказывается локальная конечность произвольных 2-групп с двупорождёнными конечными подгруппами и даётся их исчерпывающее описание.

[1] Д. В. Лыткина, В. Д. Мазуров О 2-группах с конечными подгруппами ранга 2. // Сибирск. математический журнал,
т. 57, № 3 (2016), 675-682.

3. Завершено описание почти простых групп, цоколь которых является простой исключительной группой лиева типа, изоспектральных своему цоколю.

Группы называются изоспектральными, если их множества порядков элементов совпадают. Как было установлено несколько лет назад, если S – конечная простая исключительная группа лиева типа, отличная от 3D_4(2), то любая конечная группа G, изоспектральная S, является почти простой группой с цоколем S. Более того, если S отлична от групп F_4(q), 3D_4(q), E_6(q), 2E_6(q) и E_7(q), то G изоморфна S. Мы описываем строение группы G во всех оставшихся случаях и, в частности, показываем, что G не всегда изоморфна S. Наше описание завершает исследование конечных групп, изоспектральных простым исключительным группам лиева типа.

[1] M. A. Grechkoseeva, M. A. Zvezdina On spectra of automorphic extensions of finite simple groups F_4(q) and ^3D_4(q)
// J. Algebra Appl., Vol. 15, No. 4, 1650168 (13 pages), 2016.
[2] М. А. Звездина О спектрах автоморфных расширений конечных простых исключительных групп лиева типа
// Алгебра и логика, т. 55, №5, 2016.

4. Построен аналог группы Линдона для свободной группы в категории про-p групп.

В 1960 году Линдон изучая уравнения от одной переменной над свободными группами, ввел понятие степенной группы F^Z[t] и показал, что эта группа дискриминируется свободными группами. В 1996 году А. Г. Мясников и В. Н. Ремесленников дали описание степенной группы с помощью понятия итерированного расширения централизаторов. Этот подход открыл очень удобное описание для алгебраической структуры конечнопорожденных подгрупп степенной группы: они получаются из свободных абелевых групп конечного ранга с помощью операций свободного произведения, амальгамированных произведений и HNN расширений. Авторы выдвинули гипотезу, что степенная группа F^Z[t] содержит в себе все предельные группы для свободных групп. Эта гипотеза была доказана О. Харлампович и А. Г. Мясниковым в 1998 г. и позднее другим способом Sela и Charmpetier-Guirardel. Есть большие основания предполагать, что соответствующие результаты будут верны и для свободных про-p групп и базой для них будет полученный результат.

[1] Montserrat Casals-Ruiz, Ilya Kazachkov, Vladimir Remeslennikov Pro-Hall R-groups and groups discriminated by the free pro-p group. // Journal of Group Theory. 2016. Volume 19, Issue 3. Pages 391–403, ISSN (Online) 1435-4446, ISSN (Print) 1433-5883, DOI: 10.1515/jgth-2016-0505, 2016. 2016. Vol. 12. P. 267-291. http://dx.doi.org/10.17377/semi.2016.12.022.

5. Охарактеризованы функции, вычислимые на машинах Блюм-Шуба-Смэйла, работающих в бесконечном времени.

С помощью итерированных тьюринговых скачков дана характеризация и предложена нормальная форма для функций, вычислимых на машинах Блюм-Шуба-Смэйла, работающих в бесконечном времени. Доказано, что множество ITBM--вычислимых вещественных чисел совпадает с вещественными числами из $L_{\omega^\omega}$ в конструктивной теоретико-множественной иерархии, что отвечает на вопрос П. Кёпке.

[1] П. Кёпке, А. С. Морозов О вычислительных возможностях машин Блюм-Шуба-Смэйла, работающих в бесконечном времени. // Алгебра и логика, 2016, Т. 55, Вып. 6.

6. Введено отношение обобщенно гиперарифметической сводимости на структурах, порождающее соответствующие полурешетки степеней структур. Установлено естественное вложение в эти полурешетки полурешетки гиперстепеней множеств натуральных чисел, сохраняющее операцию гиперскачка. Получено синтаксическое описание структур, имеющих гиперстепень.

Рассматривается класс аппроксимационных пространств Ершова-Скотта, порожденных допустимыми множествами и, в частности, наследственно конечными надстройками над структурами. Обобщенная вычислимость на аппроксимационных пространствах понимается как эффективная определимость в динамической логике. Аналогично понятию структуры, Сигма-определимой в допустимом множестве, вводится понятие эффективной определимости структуры на аппроксимационном пространстве, а также отношение сводимости на структурах, порождающее соответствующие полурешетки степеней структур. Установлено естественное вложение в эти полурешетки полурешетки гиперстепеней множеств натуральных чисел, сохраняющее операцию гиперскачка. В терминах определимости в динамической получено синтаксическое описание структур, имеющих гиперстепень, дополняющее аналогичные результаты из [1,2].

[1] А. И. Стукачев О степенях представимости структур. I // Алгебра и логика. 2007. Т. 46. № 6. C. 763-788.
[2] А. I. Stukachev Effective model theory: an approach via $\Sigma$-definability // In N. Greenberg, D. Hirschfeldt, J.D. Hamkins, and R. Miller (Eds.): Effective Mathematics of the Uncountable, Cambridge University Press, 2013, 204 p. [Lecture Notes in Logic Series, V. 41]. P. 164-197.
[3] А. I. Stukachev On processes and structures // Lecture Notes in Computer Science. 2013. V. 7921. P. 393-402.
[4] А. И. Стукачев Обобщенно гиперарифметическая вычислимость над структурами. // Алгебра и логика. 2016. Т. 55,
№ 5. С. 538-561.

7. Решена проблема табличности над минимальной логикой Йохансона.

Решена проблема табличности над минимальной логикой J Йохансона: указан алгоритм, позволяющий по любой конечной системе аксиом установить, является ли J-логика с этими аксиомами табличной.
Логика называется табличной, если она может быть задана с помощью конечной модели; логика предтаблична, если она нетаблична, но все ее собственные расширения табличны.
Логика является табличной, если и только если она не содержится ни в одной из предтабличных логик.
Доказано, что существуют точно семь предтабличных расширений минимальной логики, все они полностью описаны, найдена их аксиоматизация и семантическая характеризация. Доказано, что все предтабличные логики узнаваемы над J, указаны соответствующие алгоритмы. Доказана разрешимость проблемы табличности над минимальной логикой, показана NP-полнота проблемы табличности над J.

[1] Л. Л. Максимова, В. Ф. Юн Проблема табличности над минимальной логикой. // СМЖ. 2016. Т. 57, № 6. С. 1320–1332.

8. Получено полное описание степеней автоустойчивости для ординалов и почти суператомных булевых алгебр. Доказано, что для любого вычислимого ординала α существует разрешимая булева алгебра, имеющая степень автоустойчивости относительно сильных конструктивизаций 0^(α).

Одним из важных вопросов теории вычислимых моделей является проблема алгоритмической сложности изоморфизмов между алгебраическими системами. Тьюрингова степень d является степенью автоустойчивости вычислимой модели M, если d – это наименьшая из степеней, могущих вычислять изоморфизм между произвольными вычислимыми копиями М. Понятие степени автоустойчивости дает количественную оценку для сложности изоморфизмов. В работе дано полное описание степеней автоустойчивости для вычислимых ординалов и почти суператомных булевых алгебр. Доказано, что для любого вычислимого ординала α существует разрешимая атомная булева алгебра, имеющая степень автоустойчивости относительно сильных конструктивизаций 0^(α). Построена новая серия примеров степеней автоустойчивости для линейных порядков и линейно упорядоченных абелевых групп.

[1] Н. А. Баженов О степенях автоустойчивости относительно сильных конструктивизаций для булевых алгебр
// Алгебра и логика, 2016, Т. 55, № 2, 133-155.
[2] Н. А. Баженов О степенях автоустойчивости для линейных порядков и линейно упорядоченных абелевых групп
// Алгебра и логика, 2016, Т. 55, № 4, 393-418.

9. Найдены важные геометрические объекты для одного класса групп Ли с субримановой метрикой.

В работе [1] найдены основные геометрические объекты для всех групп Ли, локально изометрично накрывающих группу Ли SO_2(2,1) с левоинвариантной субримановой метрикой, инвариантной относительно правых сдвигов на элементы подгруппы SO(2).

[1] В. Н. Берестовский, И. А. Зубарева Локально изометричные накрытия группы Ли SO_0(2,1) со специальной субримановой метрикой // Мат. сб. 2016. Т. 207, № 9. С. 3-24.

10. Построен начальный список трехмерных гиперболических многообразий, допускающих построение из правильных идеальных тетраэдров пространства Лобачевского. Распознаны многообразия, являющиеся дополнениями к зацеплениям в трехмерной сфере.

Получены новые результаты о классификации трехмерных многообразий. Трехмерное гиперболическое многообразие называется тетраэдральным, если оно может быть склеено из правильных идеальных тетраэдров пространства Лобачевского. Тетраэдральные многообразия являются некомпактными и имеют максимальный объём среди всех трехмерных гиперболических многообразий, построенных из фиксированного числа произвольных тетраэдров. В [1] с существенным использованием компьютерных методов построены ориентируемые (до 25 тетраэдров) и неориентируемые (до 21 тетраэдра) тетраэдральные многообразия. Число многообразий первого типа равно 11580, а второго – 25184. Доказано, что все тетраэдральные многообразия являются арифметическими и соизмеримы с дополнением к узлу восьмерка. Установлено, какие из построенных тетраэдральных многообразий являются гомологическими зацеплениями и распознаны те их них, которые являются дополнениями к зацеплениям в трехмерной сфере. На рисунке приведены восемь зацеплений в трехмерной сфере, дополнения к которым являются тетраэдральными многообразиями, склеиваемыми из 10 правильных идеальных тетраэдров.

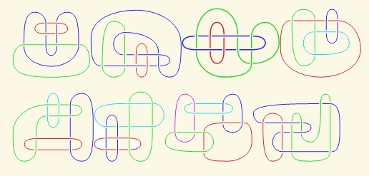
[1] E. Fominykh, S. Garoufalidis, M. Goesner, V. Tarkaev, A. Vesnin A census of tetrahedral hyperbolic manifolds // Experimental Mathematics, 2016, 25:4, 466-481.

11. Получена оценка хаусдорфовой размерности семейства «плохих» гиперплоскостей E_α, на которых следы функций из пространства Соболева W^1,p(Rⁿ) (n-1<p<n) не удовлетворяют условию Гельдера с показателем α

При p ≤ n пространство Соболева W^1,p(Rⁿ) содержит разрывные функции, но при n-1<p ≤ n на почти всех гиперплоскостях ортогональных некоторой оси следы таких функций непрерывны и удовлетворяют условию Гельдера с показателем α_p=1-(n-1)/p. Пусть 0<α< α_p и E_α – исключительное семейство гиперплоскостей S_t={x∈Rⁿ;x_n=t}, на которых следы функции u∈W^1,p(Rⁿ) (n-1<p<n) не удовлетворяют условию Гельдера с показателем α. Пусть для всех t∈F_α гиперплоскости S_t∈E_α, тогда хаусдорфова размерность dim_H(F_α) ≤ n-(1- α)p<1 и при изменении α от 0 до α_p размерность dim_H(F_α) меняется от n-p до 1. Получены оценки ``массивности´´ α-исключительного семейства липшицевых гиперповерхностей Ʃ_α в терминах p-модулей. Если 0<α<α_p и q=p(1- α)/(n-1), то Mod_q(Ʃ_α)=0.
В предельном случае p=n-1 для соболевских функций, у которых градиент принадлежит пространству Лоренца
L_n-1,1(Rⁿ), доказана (n-1)-абсолютная непрерывность следов на почти всех гиперплоскостях ортогональных некоторой оси.

[1] А. С. Романов О непрерывности соболевских функций на гиперплоскостях.//Сиб. элект. матем. изв., 2015, Т. 12,
832-841.
[2] А. С. Романов О гельдеровости соболевских функций на гиперповерхностях. //Сиб. элект. матем. изв., 2016, Т. 13, 624-634.

12. Построена теория слабой сходимости для сильных материалов с p(x)-ростом.

В последние 15 лет в литературе интенсивно изучаются вариационные задачи

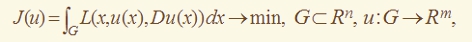
в которых каратеодориевы интегранды L имеют p(x)-рост по Du:


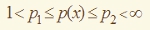
Изучается теория слабой сходимости для таких функционалов: полунепрерывность функционалов снизу относительно слабой сходимости в соболевском пространстве, свойство сходимости в энергии, построение полунепрерывной снизу оболочки исходного функционала. Многие известные авторы получали различные результаты в предположении, что p(x) − непрерывная функция, удовлетворяющая классическому условию В. В. Жикова, что обеспечивает возможность аппроксимировать в энергии соболевские функции гладкими. М. А. Сычевым показано, что в случае сильных материалов (p₁>n) теорию слабой сходимости можно построить без этого условия.

[1] M. A. Sychev, N. N. Sycheva Young measure approach to the weak convergence theory in the calculus of variations and strong materials // Annalidella Scuola Normale Superiore di Pisa, Classe di Scienze, Serie V, Vol. XV, 2016, 561-598.

13. Получено эквивалентное описание измеримых отображений, индуцирующих по правилу замены переменной изоморфизмы классов Соболева на группах Карно.

Изучаются метрические свойства измеримых отображений на группе Карно, индуцирующих по правилу замены переменной изоморфизмы пространств Соболева. Доказано, что такое отображение можно переопределить на множестве меры нуль так, что оно будет либо квазиконформным, когда показатель суммируемости совпадает с хаусдорфовой размерностью группы, либо квазиизометрическим, когда показатель суммируемости отличен от хаусдорфовой размерности группы.

[1] С. К. Водопьянов, Н. А. Евсеев Изоморфизмы соболевских пространств на группах Карно и квазиизометрические отображения // Сиб. мат. журн. 2014. Т. 55, № 5. C. 1001-1039. DOI: 10.1134/S0037446614050048
[2] С. К. Водопьянов, Н. А. Евсеев Изоморфизмы соболевских пространств на группах Карно и метрические свойства отображений // Докл. АН. 2015. Т. 464, № 2. С.131-135. DOI: 10.1134/S1064562415050117
[3] С. К. Водопьянов, Н. А. Евсеев Изоморфизмы соболевских пространств на группах Карно и квазиконформные отображения // Сиб. мат. журн. 2015. Т.56, № 5. C. 989-1029. DOI: 10.1134/S0037446615050018

14. Для класса пространственноподобных поверхностей-графиков на двуступенчатых четырехмерных сублоренцевых структурах установлена формула площади, а также получены описания базовых свойств максимальных поверхностей, в том числе, и в терминах сублоренцевой средней кривизны.

Сублоренцевы структуры являются субримановым обобщением геометрии Минковского. Неформально, в такой геометрии квадрат расстояния вдоль некоторых направлений может быть отрицательным. Интерес представляет геометрия времениподобных поверхностей, для которых имеет смысл найти их площадь. Содержательная часть работы состоит в том, чтобы вывести формулу площади таких поверхности и найти ее первую вариацию.

[1] М. Б. Карманова Формула площади графиков на 4-мерных 2-ступенчатых сублоренцевых структурах // Сиб. мат. журн., 2015. Т. 56, № 5. С. 1068-1091.
[2] М. Б. Карманова Максимальные поверхности-графики на 4-мерных 2-ступенчатых сублоренцевых структурах // Сиб. мат. журн., 2016. Т. 57, № 2. С. 350-363.

15. Получены явные формулы для подсчета корневых гиперкарт на поверхностях малого рода.

В [1] получены явные формулы для подсчета корневых гиперкарт на ориентируемой поверхности рода g<4. Число гиперкарт выражается через количество направленных полуребер — дартов. Для случаев g=1 и g=2 соответствующие формулы были получены ранее в работах Walsh (1975) и Arquès (1987). В работе [1] авторы применили метод Егорычева для подсчета комбинаторных сумм для получения новой версии формулы Arquès для случая g=1. Затем указанный подход был использован для получения формул при g=2, 3. В последних двух случаях указанный метод также опирается на недавние результаты Georgetti, Walsh, Казаряна и Зографа, которые получили две различных, но эквивалентных формы для порождающих функций гиперкарт рода 2 и 3.

[1] A. D. Mednykh, R. Nedela Counting hypermaps by Egorychev’s method // Analysis and Mathematical Physics, 2016, Vol. 6, № 3, p. 301-314.

16. Исследована обратная задача рассеяния о восстановлении коэффициента преломления в обобщенном уравнении Гельмгольца по заданному модулю рассеянного поля. Она сведена к решению известной обратной кинематической задачи, что дает возможность эффективного построения искомого коэффициента.

В приложениях довольно часто возникают задачи визуализации микроструктур размером порядка микрона. Обычно для этого используется оптическая радиация с длиной волны менее одного микрона. Хорошо известно, что только интенсивность соответствующего рассеянного волнового комплексного поля может быть измерена для таких малых длин волн. В связи с этим, возникает обратная задача для волнового уравнения в частотной области (а фактически, для обобщенного уравнения Гельмгольца) об определении коэффициента преломления среды по заданному модулю рассеянного поля. Ранее подобная задача об определении потенциала рассматривалась для уравнения Шредингера. Новая постановка обратной задачи для обобщенного уравнения Гельмгольца существенно отличается от обратной задачи квантовой рассеяния на потенциале тем, что искомый коэффициент здесь стоит множителем при квадрате частоты. Это сильно усложняет ее исследование. Полученный результат состоит в построении асимптотики рассеянного поля на высоких частотах и сведения исходной обратной задачи к хорошо известной обратной кинематической задаче. Это приводит к теоремам единственности и оценкам устойчивости решения, а также открывает путь ее конструктивного решения. Рассмотрен также и линейный вариант этой задачи. Линеаризация обратной задачи сводит ее к некоторой задаче интегральной геометрии, для которой установлена теорема единственности и предложен алгоритм решения.

[1] V. G. Romanov Some geometric aspects in inverse problems // Eurasian J. of Mathematical and Computer Applications. 2015. Vol. 3, No. 4, p. 68-84. http://ejmca.enu.kz/images/stories/4issue/romanovvg.pdf
[2] M. V. Klibanov, V. G. Romanov Two reconstruction procedures for a 3D phaseless inverse scattering problem for the generalized Helmholtz equation // Inverse Problems, 2016. Vol 32, No. 2, 015005 (16pp). DOI: 10.1088/0266-5611/32/1/015005. Web of Sciences. Импакт-фактор 2.33, https://www.researchgate.net/journal/0266-5611_Inverse_Problems
[3] M. V. Klibanov, V. G. Romanov Reconstruction procedures for two inverse scattering problem without the phase information // SIAM J. Appl. Math., Vol. 76, No. 1, p. 178-196. DOI: 10.1137/15M1022367. Web of Sciences. Импакт-фактор 1.51, https://www.researchgate.net/journal/0036-1399_SIAM_Journal_on_Applied_Mathematics

17. Установлены новые критерии экспоненциальной дихотомии для систем линейных дифференциальных и разностных уравнений с периодическими коэффициентами. Получены оценки параметров дихотомии. Доказаны теоремы о возмущении для экспоненциальной дихотомии.

В работах [1, 2] решен ряд задач об экспоненциальной дихотомии для систем линейных дифференциальных уравнений и разностных уравнений с периодическими коэффициентами. При решении этих задач были поставлены и изучены новые краевые задачи двух типов: а) для дифференциального уравнения Ляпунова; б) для системы разностных уравнений Ляпунова. Для этих краевых задач доказаны теоремы существования решений и описаны классы единственности решений. На основе полученных результатов установлены новые критерии экспоненциальной дихотомии для дифференциальных и разностных уравнений с периодическими коэффициентами. Используя решения краевых задач, получены оценки параметров дихотомии. Рассмотрены системы линейных дифференциальных и разностных уравнений с возмущениями коэффициентов. Получены достаточные условия на возмущения, при которых сохраняется экспоненциальная дихотомия. Доказательство теорем о возмущении основано на полученных оценках параметров дихотомии. В случае постоянных коэффициентов полученные результаты являются аналогами теорем
М. Г. Крейна, С. К. Годунова и А. Я. Булгакова.

[1] G. V. Demidenko On conditions for exponential dichotomy of systems of linear differential equations with periodic coefficients // Int. J. Dynamical Systems and Differential Equations. 2016. V. 6, No. 1. P. 63-74.
[2] Г. В. Демиденко, А. А. Бондарь Экспоненциальная дихотомия систем линейных разностных уравнений с периодическими коэффициентами // Сиб. мат. журн. 2016. Т. 57, № 6. С. 1240-1254.

18. Изучено строение фазовых портретов широкого класса нелинейныхдинамических систем химической кинетики. Описаны их стационарные точки. Получены условия существования циклов, в том числе неустойчивых. Построены их инвариантные окрестности, ретрагирующиеся на эти циклы. Полученные результаты и разработанные подходы послужили основой построения адекватных моделей ряда биологических процессов.

Исследовано комбинаторное и геометрическое строение фазовых портретов ряда динамических систем, моделирующих функционирование генных сетей, построены инвариантные поверхности этих систем, описаны их стационарные точки. Получены условия существования циклов, в том числе неустойчивых, построены инвариантные окрестности устойчивых циклов. Для систем размерности 4 обнаружены нетривиальные зацепления (зацепление Хопфа) циклов и инвариантных поверхностей, см. рисунок. Полученные результаты и разработанные подходы послужили основой построения адекватных моделей биологических процессов, происходящих на раннем этапе развития плодовой мушки D.melanogaster.

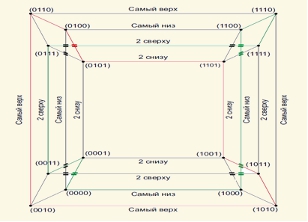
Зацепление Хопфа в одномерном остове четырехмерного куба.

[1] Н. Б. Аюпова, В. П. Голубятников О двух классах нелинейных динамических систем. Четырехмерный случай. // Сибирский математ. журнал. 2015, т. 56, N 2, с. 282 – 289.
[2] В. П. Голубятников, А. Э. Калёных О строении фазовых портретов некоторых нелинейных динамических систем. //Вестник НГУ, серия Математика, механика, информатика. 2015, т. 15, N 1, с. 45 – 53.
[3] T. A. Bukharina, D. P. Furman, V. P. Golubyatnikov A model study of the morphogenesis of D. melanogaster mechanoreceptors: The central regulatory circuit. // Journal of Bioinformatics and Computational Biology. February 2015,
v. 13, N. 01, DOI: 10.1142/S0219720015400065, p. 1540006-1 – 1540006-15. (15 страниц)
[4] T. A. Bukharina, D. P. Furman, V. P. Golubyatnikov Gene network controlling morphogenesis of D. melanogaster macrochaetes: an expanded model. // Russian Journal of Development Biology. 2016. V. 47, N 5. P. 288 – 293.
[5] А. А. Акиньшин, Т. А. Бухарина, В. П. Голубятников, Д. П. Фурман Математическое моделирование взаимодействия двух клеток в пронейральном кластере крылового имагинального диска D.melanogaster. // Вестник НГУ, 2014, т. 14,
N 4, с. 3–10.

19. Для системы уравнений Навье-Стокса несжимаемой жидкости в трехмерном полупространстве доказано существование прямых (по времени) автомодельных (=самоподобных) решений для сколь угодно больших самоподобных исходных данных.

Для системы уравнений Навье-Стокса несжимаемой жидкости в трехмерном полупространстве доказано [1] существование прямых (по времени) автомодельных (=самоподобных) решений для сколь угодно больших самоподобных исходных данных. (Решение уравнений Н.-С. называется самоподобным, если выполняется тождество u(x,t)=s u(sx,s^2t) для всех положительных параметров s.) Данный результат является дополнением классической теоремы Нечаса, Ружички и Шверака [2] о НЕ существовании обратных повремени самоподобных решений системы Н.-С. Для доказательства применяются методы «от противного», которые недавно помогли решить [3] проблему Лерэ о существовании решений краевой задачи для стационарной системы уравнений Н.-С.

[1] M. V. Korobkov, T.-P. Tsai Forward Self-Similar Solutions of the Navier-Stokes Equations in the Half Space // Analysis and PDE, Vol.9, No.8 (2016).
[2] J. Necas, M. Ruzicka, V. Sverak On Leray’s self-similar solutions of the Navier-Stokes equations // Acta Math. 176 (1996), 283–294.
[3] M. V. Korobkov, K. Pileckas, R. Russo Solution of Leray's problem for stationary Navier-Stokes equations in plane and axially symmetric spatial domains // Ann. of Math., 181, No. 2 (2015), 769–807. http://dx.doi.org/10.4007/annals.2015.181.2.7

20. Получены новые асимптотические результаты в граничных задачах для случайных блужданий и обобщенных процессов восстановления.

1. Найдена аппроксимация второго порядка в так называемых переходных явлениях для систем обслуживания при большой нагрузке, когда среднее значение приращения соответствующего процесса отрицательно и мало. Одновременно найдено простое доказательство аппроксимации первого порядка (теоремы Кингмана-Прохорова) об экспоненциальности предельного распределения в переходных явлениях [1].
2. Найдено предельное распределение времени первого прохождения произвольной удаленной границы траекторией случайного блуждания [2].
3. Получены интегральные теоремы для времени первого прохождения произвольной границы обобщенным процессом восстановления [3].
4. Установлен принцип больших уклонений в граничных задачах для обобщенных процессов восстановления [4].

[1] А. А. Боровков Теоремы непрерывности и асимптотика второго порядка в переходных явлениях для граничных функционалов от случайных блужданий // Математические труды. 2016. Т. 19, вып.1. С. 46-69.
[2] А. А. Боровков О распределении времени первого прохождения случайным блужданием произвольной удаленной границы // Теория вероятностей и ее применения. 2016. Т. 61, вып. 2. С. 210-233.
[3] А. А. Боровков Интегральные теоремы для времени первого прохождения произвольной границы обобщенным процессом восстановления // Сибирский математический журнал. 2015. Т. 56, вып. 5. С. 961-981.
[4] А. А. Боровков Принципы больших уклонений в граничных задачах для обобщенных процессов восстановления // Сибирский математический журнал. 2016. Т. 57, вып. 3. С. 562-595.

21. Предложены алгоритмы построения полиномиальных сплайнов в общей задаче интерполяции. Установлены оценки погрешности интерполяции через нормы обратных матриц рассматриваемых систем уравнений для построения сплайнов.

Рассматривается общая задача полиномиальной сплайн-интерполяции. Имеем сетку узлов $\Delta$, в узлах которой известны значения некоторой функции. Требуется построить полиномиальный сплайн $s(x)$ степени $n$ наименьшего дефекта 1, т.е. гладкости $C^{n-1}$ (простой сплайн), проходящий через заданные значения. В классической задаче полиномиальной сплайн-интерполяции предполагается если степень $n$ нечётная, то узлы сплайна $s(x)$ совпадают с заданными точками интерполяции; если $n$ чётно, то классическими можно назвать две конструкции: по Субботину - узлы сплайна расположены строго посреди между точками интерполяции, и по Марсдену - точки интерполяции расположены строго посреди узлов сплайна. В работе рассмотрена общая задача интерполяции, т.е. помимо сетки $\Delta$ точек интерполяции задана ещё одна сетка $\delta$, сетка узлов сплайна $s(x)$ степени $n$, интерполирующего заданные значения.
Простой сплайн $s(x)$, являющийся решением общей задачи интерполяции, является нелокальным (при $n>1$) и его построение заключается в нахождении каких-либо параметров сплайна, через которые можно выразить сплайн. Задача определения таких параметров сводится к решению системы линейных уравнений. От выбора параметров сплайна зависят свойства получаемых систем уравнений.
Ранее автором был предложен подход к построению классических интерполяционных сплайнов произвольной нечётной степени, состоящий в том, что в качестве определяемых параметров сплайна выбираются коэффициенты разложения какой-либо производной сплайна по нормализованным $B$-сплайнам соответствующей степени.
При этом получение таких систем не составляет особого труда. Интересно отметить, что предложенный подход привёл к новому устойчивому способу построения даже кубических сплайнов, несмотря на их достаточно детальную изученность. В дальнейшем были изучены свойства матриц получаемых при таком подходе систем уравнений, была установлена связь обусловленности этих матриц с вопросами сходимости процессов интерполяции для соответствующих производных и, как следствие, выделены методы с хорошо обусловленными системами уравнений.
В работе этот подход распространяется на общую задачу полиномиальной сплайн-интерполяции, изучаются свойства матриц получаемых систем уравнений, оценивается погрешность интерполяции.

[1] Ю. С. Волков Обусловленность систем уравнений построения сплайнов и сходимость процессов сплайн интерполяции // Труды Международной летней математической Школы-Конференции С. Б. Стечкина по теории функций / Ред.: М. Ш. Шабозов, А. Г. Бабенко, М. В. Дейкалова. Душанбе: Офсет, 2016. C. 78-81.
[2] Ю. С. Волков Общая задача полиномиальной сплайн-интерполяции // Труды Института математики и механики УрО РАН. 2016. Т. 22, № 4. 12 с.

22. Построена математическая модель, описывающая эволюцию сорбционных и текстурных свойств сорбентов на основе оксида кальция в процессе многократного повторения циклов сорбции/регенерации.

Построена математическая модель, описывающая эволюцию сорбционных и текстурных свойств сорбентов на основе оксида кальция в процессе многократного повторения циклов сорбции/регенерации. Модель учитывает морфологические особенности сорбента, физику его спекания и кинетику сорбции диоксида углерода. Структура сорбента описывается случайной плотной упаковкой сфер, спекание моделируется динамикой упаковки, геометрические характеристики которой связаны с сорбционными свойствами оксида кальция. Полученная модель позволяет вычислить динамику емкостных характеристик сорбента в зависимости от номера цикла сорбции/регенерации и находится в хорошем соответствии с экспериментальными данными. Она может быть использована для нахождения как оптимальной структуры сорбента, так и для оптимального режима проведения сорбции/регенерации.

Согласованность модели и эксперимента для циклов сорбции/регенерации, проходящих при разной продолжительности времени сорбции (7.5 мин и 30 мин). На 80-м и 100-м циклах происходит переключение времен сорбции.

[1] Ya. V. Bazaikin, V. S. Derevschikov, A. I. Lysikov, E. G. Malkovich, A. G. Okunev Evolution of sorptive and textural properties of CaO-based sorbents during repetitive sorption/regeneration cycles // Chemical Engineering Science. 2016. Volume 152, Pages 709–716.

23. Получено разложение симметричного m-тензорного поля, заданного в круге, в сумму (m+1)-го поля, каждое из которых определяется одним потенциалом. С использованием этого разложения описаны свойства лучевых преобразований, действующих на симметричные m-тензорные поля. Получены формулы обращения.

Теоремы разложения на соленоидальную и потенциальную части играют важную роль в векторной и тензорной томографии. В двумерном случае авторами получено детальное разложение симметричного m-тензорного поля. Показано, что любое такое поле можно представить в виде суммы одного соленоидального и m потенциальных полей, каждое из которых определяется одним потенциалом (функцией). Разложение единственно при наложении на потенциалы граничных условий. Полученное разложение послужило основой для описания свойств операторов лучевых преобразований, действующих на тензорные поля. Описаны ядра и образы операторов смешанных и поперечных лучевых преобразований. Установлены связи между лучевыми преобразованиями тензорных полей и преобразованиями Радона их потенциалов. Получены формулы обращения, дающие как компоненты полей, так и их потенциалы. Доказаны проекционные теоремы и оценки устойчивости для операторов лучевых преобразований. Результаты легли в основу ряда алгоритмов тензорной томографии.

[1] Е. Ю. Деревцов Некоторые задачи нескалярной томографии. // Сибирские Электронные Математические Известия. Труды первой международной молодежной школы-конференции ``Теория и численные методы решения обратных и некорректных задач´´. Часть I. 2010, Т. 7, С.81-С.111.
[2] I. E. Svetov Properties of the ray transforms of two-dimensional 2-tensor fields defined in the unit disk. // Journal of Applied and Industrial Mathematics, 2014, Vol. 8, No. 1, P. 106-114. DOI:10.1134/S1990478914010128
[3] E. Yu. Derevtsov, I. E. Svetov Tomography of tensor fields in the plain. // Eurasian journal of mathematical and computer applications, 2015, Vol. 3, No. 2, P. 24-68.
[4] И. Е. Светов, С. В. Мальцева, А. П. Полякова Приближенное обращение операторов двумерной векторной томографии. // Сибирские электронные математические известия, 2016, Т. 13, С. 607-623.

24. Построен приближённый алгоритм синтеза энергоэффективных беспроводных сетей.

Энергозатраты на радиопередачу пропорциональны дальности передачи. В распределённых беспроводных сетях сбора и передачи данных, например, в сенсорных сетях, собранная элементами сети информация передаётся в базовую станцию, которой (в разное время) может быть любой элемент сети. При синтезе коммуникационного графа требуется определить связный неориентированный остовный подграф, энергозатраты на поддержания которого минимальны. Математическая постановка задачи может быть сформулирована следующим образом. Дан простой неориентированный взвешенный связный граф G=(V,E), каждому ребру (i,j)∈E которого приписано неотрицательное действительное число c_ij. Требуется найти остовное дерево T*, которое является решением задачи:

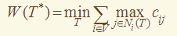
где N_i(T) – множество вершин смежных с вершиной i в дереве T.
Это хорошо известная в комбинаторной оптимизации задача, известная как Min-Power Symmetric Connectivity Problem, которая NP-трудна в сильном смысле даже в случае, когда веса рёбер принимают всего два значения.
С другой стороны, известно, что минимальное остовное дерево является 2-приближённым решением задачи. Нами получены априорные оценки точности, определены границы неаппроксимируемости, найдены частные случаи полиномиальной разрешимости, а также разработаны приближенные алгоритмы, в основе которых лежит, в частности, метод локального поиска с чередующимися окрестностями (Variable Neighborhood Search – VNS). Проведён апостериорный анализ алгоритмов, показавший высокую эффективность нашего метода. Для примеров небольшой размерности (до 30 вершин) почти всегда находится оптимальное решение. Построенные решения для задач большой размерности не удаётся сравнить с оптимальным решением (оно неизвестно), но полученные результаты являются рекордными по точности.

[1] A. Erzin, R. Plotnikov, N. Mladenovic Variable neighborhood search variants for Min-power symmetric connectivity problem // Computers & Operations Research, 2016, doi:10.1016/j.cor.2016.05.010 (Web of Science IF=1.8, Scopus)
[2] R. V. Plotnikov, A. I. Erzin, N. Mladenovic Variable Neighborhood Search-Based Heuristics for Min-Power Symmetric Connectivity Problem in Wireless Networks // In: Kochetov, Yu. et all (eds.) DOOR-2016. LNCS, vol. 9869, pp. 220–232, Springer, Heidelberg (2016), DOI: 10.1007/978-3-319-44914-2 18 (Web of Science, Scopus)
[3] R. V. Plotnikov, A. I. Erzin, N. Mladenovic Approximation Algorithms for the Min-Power Symmetric Connectivity Problem // AIP Conference Proceedings 1776, 050012 (2016); doi: 10.1063/1.4965333 (Web of Science)
[4] A. Erzin, R. Plotnikov Using VNS for the Optimal Synthesis of the Communication Tree in Wireless Sensor Networks // Electronic Notes in Discrete Mathematics, 2015, 47, 21-28, DOI: 10.1016/j.endm.2014.11.004 (Scopus)
[5] А. И. Ерзин, Р. В. Плотников, Ю. В. Шамардин О некоторых полиномиально разрешимых случаях и приближенных алгоритмах для задачи построения оптимального коммуникационного дерева // Дискретный анализ и исследование операций, Т. 20, № 1, 2013, 12-27.

25. Исследована вычислительная сложность нескольких евклидовых задач оптимального суммирования векторов. Доказана NP-трудность задач, и установлены случаи их псевдополиномиальной разрешимости.

Исследована вычислительная сложность нескольких известных дискретных экстремальных задач с измененным направлением оптимизации, а именно: c max на min. В этих задачах требуется в конечном множестве векторов найти подмножества, доставляющие минимум целевым функциям, которые зависят либо только от нормы суммы элементов подмножества, либо от этой нормы и мощности искомого подмножества. Задачи имеют приложения в физике, статистике, электроэнергетике и индуцируются проблемами интерпретации данных (Datamining). Доказано, что если размерность пространства является частью входа, то все рассмотренные задачи NP-трудны в сильном смысле. Установлено, что при фиксированной размерности пространства все задачи NP-трудны даже в двумерном случае (на плоскости) и для них не существует приближенных алгоритмов с гарантированной оценкой точности, если P≠NP. В одномерном случае (на прямой) доказана NP-трудность задачи без ограничения на мощность кластера. С другой стороны, показано, что если координаты входных векторов целочисленны, то все задачи разрешимы за псевдополиномиальное время в случае, когда размерность пространства фиксирована (ограничена сверху константой). Для случая, когда размерность пространства не фиксирована, предложен метод решения задач с использованием моделей целочисленного программирования.

[1] А. В. Еремеев, А. В. Кельманов, А. В. Пяткин О сложности некоторых евклидовых задач оптимального суммирования. Доклады Академии наук. Т. 468, N 4. 2016. С. 372-375. DOI: 10.7868/S0869565216160039
[2] А. В. Еремеев, А. В. Кельманов, А. В. Пяткин О сложности и аппроксимируемости некоторых евклидовых задач оптимального суммирования. Журнал вычислительно математики и математической физики, 2016, том 56, № 10,
с. 142-147. DOI: 10.7868/S0044466916100082

26. Доказано, что класс функций Голда содержит первую бесконечную серию примеров почти совершенно нелинейных функций, чей класс дифференциальной эквивалентности шире, чем тривиальный.

Почти совершенно нелинейной (APN) функцией называется векторная булева функция F от n переменных, для которой уравнение F(x)+F(x+a)=b имеет не более двух решений для любых двоичных векторов a и b, где a – ненулевой. APN-функции представляют интерес для использовании в криптографических алгоритмах в качестве узлов замены в силу своих оптимальных дифференциальных характеристик. Вопрос о полном описании класса APN-функций является открытым. Для F известным образом определяется ассоциированная булева функция gF от 2n переменных по правилу: gF(a,b)=1, если уравнение F(x)+F(x+a)=b имеет решение и a – ненулевой вектор, и gF(a,b)=0 иначе. В данной работе введено понятие дифференциально эквивалентных векторных булевых функций как функций, имеющих одинаковые ассоциированные булевы функции. Вопрос об описании класса эквивалентности произвольной APN-функции является открытым и представляет интерес, поскольку его решение может привести к построению новых APN-функций. В работе полностью описаны аффинные функции, сложение которых с функциями из известного класса квадратичных APN-функций Голда не выводит за рамки их классов дифференциальной эквивалентности. Показано, что класс функций Голда содержит первую бесконечную серию примеров APN-функций, чей класс дифференциальной эквивалентности шире, чем тривиальный.

[1] А. А. Городилова От криптоанализа шифра к криптографическому свойству булевой функции // Прикладная дискретная математика. 2016. № 3 (33). C. 16–44.
[2] А. А. Городилова Линейный спектр квадратичных APN-функций // Прикладная дискретная математика. 2016. № 4 (34). C. 5–16.

27. Доказано существование иммиграционно-состоятельного (устойчивого) деления на страны в многомерном пространстве (проблема в постановке Алесины и Сполаоре).

Изучается вопрос иммиграционно-состоятельного деления на страны на плоскости и в конечномерном пространстве, который ранее анализировался исключительно в одномерной постановке. Это своеобразное равновесие Тибу, где принцип миграционной состоятельности предполагает, что у пограничных жителей отсутствуют выявленные мотивы для изменения юрисдикции, т. е. в данной точке размещения населения имеется равенство издержек у граждан граничных стран. Требуется, чтобы граница была представлена непрерывной кривой (поверхностью).
Существование деления на страны установлено для измеримой плотности населения; изучались и описываются два подхода.
1) Специфическая одномерная аппроксимация, для которой находится неподвижная точка (теорема Какутани) и далее осуществляется предельный переход, — так было установлено существование деления на две страны на плоскости.
2) Общий подход, основанный на применении новой теоремы о неподвижной точке (обобщение теоремы Красносельского), — доказано существование деления на любое заданное число стран в конечномерном пространстве. Здесь частично применялись идеи из неопубликованной работы «Savvateev, A., Sorokin, C. and S.Weber (2015). Theory of spatial general equilibrium», однако представленный результат более общий и охватывает случай переменных центров.

[1] Marakulin, Valeriy M. On the existence of immigration proof partition into countries in multidimensional space // In: Kochetov, Yu. et all (eds.) DOOR-2016. LNCS (Lecture Notes in Computer Sciences), vol. 9869, pp. 494–508. Springer, Heidelberg (2016) (Scopus 0,365)
[2] Valeriy M. Marakulin Spatial general equilibrium: on immigration proof partition in multidimensional space // XXIV Европейской Школы-Семинара по Теории Общего Равновесия (European Workshop on General Equilibrium Theory (EWGET 2015)), 20 p. https://www.dropbox.com/s/4w4exn9mn7gjlnw/Marakulin.pdf?dl=0#
[3] Valeriy M. Marakulin . On the theory of spatial general equilibrium and Teibout equilibrium in multidimensional space
// 15th SAET Conference on Current Trends in Economics University of Cambridge, UK, July 27-31, 2015, 20 p. https://www.researchgate.net/profile/Valeriy_Marakulin/publications

28. Установлено взаимнооднозначное соответствие между кликовыми битрейдами в дистанционно-регулярном графе, достигающими нижней весовой оценки на мощность, и двудольными дистанционно-регулярными подграфами с определенными параметрами.

Битрейды (трейды) отражают гипотетическую разность между двумя комбинаторными конфигурациями, например блок-схемами, с одинаковыми параметрами и часто используются для построения таких конфигураций. В работе рассматриваются кликовые битрейды, обобщающие несколько известных типов битрейдов, включая латинские, Штейнеровы (k-1,k,v) и расширенные 1-совершенные битрейды. Установлено взаимнооднозначное соответствие между кликовыми битрейдами в дистанционно-регулярном графе, достигающими нижней весовой оценки на мощность, и двудольными, изометрично вложенными, дистанционно-регулярными подграфами с определенными параметрами. Как следствие, установлена минимальная мощность q-ичного Штейнерового (k-1,k,v)-битрейда и показана взаимосвязь между такими битрейдами минимальной мощности и двудольными полярными подграфами графа Грассмана Jq(v,k).

[1] D. S. Krotov, I. Yu. Mogilnykh, V. N.Potapov To the theory of q-ary Steiner and other-type trades // Discrete Mathematics. 2016. V. 339, No 3. P. 1150-1157. DOI 10.1016/j.disc.2015.11.002

29. Предсказано рождение пары адронов разделенных большим интервалом быстроты на Большом Адронном Коллайдере.

Предлагается исследовать на Большом Адронном Коллайдере (БАК) процессы рождения пар адронов в кинематической области когда детектируемые при больших поперечных импульсах адроны разделены также и большим интервалом быстроты. Такие реакции открывают новые возможности для исследования на БАК динамики сильных взаимодействий кварков и глюонов в пределе Редже. Впервые получены предсказания для сечений и угловых распределений этих процессов.

[1] Francesco G. Celiberto, Dmitry Yu. Ivanov, Beatrice Murdaca, and Alessandro Papa . High energy resummation in dihadron production at the LHC // Phys.Rev. D. 94, No. 3 (2016), 034013.