| |
Важнейшие научные результаты Института математики за 2014 год
1. Установлен критерий униформизации для наследственно конечных надстроек над моделями квазирегулярных теорий.
Наследственно конечные надстройки являются вполне адекватной математической формализацией для структуры, в которой происходит вычисление программы с заданными базовыми типами данных. Наличие в надстройке так называемого свойства униформизации позволяет утверждать наличие также важных естественных свойств, присущих классической вычислимости, в частности, наличие универсальной вычислимой функции (хорошего языка программирования над такими структурами). Автором получен критерий униформизации для наследственно конечных надстроек над моделями определенного класса теорий (так называемых квазирегулярных теорий).
Стукачев А. И. О квазирегулярных структурах вычислимых сигнатур // Сибирские электронные математические известия, - Т. 11, - 2014. - С. 444-450.
Стукачев А. И. О свойствах s-сигма сводимости // Алгебра и логика, - Т. 53, - вып. 5, - 2014.
2. Доказано, что спектр конечной простой группы лиева типа лиева ранга больше четырех отличен от спектра ее любого собственного накрытия.
Спектром конечной группы называется множество порядков ее элементов. Одним из центральных вопросов в исследовании того, насколько хорошо конечная неабелева простая группа L определяется своим спектром, является вопрос об отличии спектра группы L от спектра ее любого собственного накрытия, т.е. конечной группы гомоморфно, но не изоморфно отображающейся на L. Сложность этого вопроса обусловлена его связью с минимальными многочленами элементов группы L в ее модулярных представлениях. Решение вопроса известно для всех неабелевых простых знакопеременных групп подстановок и для всех спорадических групп. В работе доказано, что спектр конечной простой группы лиева типа, отличной от групп PSL(4,q), PSU(3,q), PSU(4,q), PSU(5,2) и тройственной группы Стейнберга над полем порядка 8, не может совпасть со спектром ее собственного накрытия
M. A. Grechkoseeva On element orders in covers of finite simple classical groups, J. Algebra 339 (2011), 304–319.
M. A. Grechkoseeva Element orders in covers of finite simple groups of Lie type, J. Algebra Appl., DOI: 10.1142/S0219498815500565
3. Получен аналог аргумента Фраттини для холловых подгрупп.
Напомним, что для данного множества простых чисел π подгруппа H группы G называется π-холловой, если порядок H делится на простые числа только из π, а индекс H в G не делится на простые числа из π. Пусть A - нормальная подгруппа конечной группы G и для некоторого множества простых чисел π группа G содержит π-холлову подгруппу. Тогда A содержит такую π-холлову подгруппу H, что G=ANG(H). Данное утверждение является одним из наиболее широко используемых в теории конечных групп и называется аргументом Фраттини.
Обоснование: Одним из важнейших применений теоремы Силова в теории конечных групп является, так называемый аргумент Фраттини. Поскольку понятие π-холловой подгруппы является прямым и наиболее естественным обобщением понятия силовской подгруппы, для теории конечных групп важно иметь аналог аргумента Фраттини для холловых подгрупп. Полученный результат является максимально общим результатом в данном направлении (любое ослабление условий или усиление заключения приводят к тому, что результат становится неверным) и открывает широкие перпективы для применения разработанной теории холловых подгрупп для изучения строения конечных групп.
Vdovin E. P., Revin D. O. Frattini argument for Hall subgroups // Journal of Algebra, 2014, v. 414, 95—104.
4. Полностью описаны все P-спектры абелевых групп для основных типов подгрупп P.
Все необходимые исторические ссылки и связанные с формулировкой представленного результата определения содержатся в статье [1]. Отметим только, что спектр S(x) называется максимальным, если S(λ) = 2λ для любого бесконечного кардинала λ.
Представленный результат состоит в следующем.
Для любой полной теории T абeлевых групп ее (P,i)-спектр для i = 1,2,3,4, где 1) сервантные подгруппы, 2) элементарные подгруппы, 3) алгебраически замкнутые подгруппы, 4) любые подгруппы, соответственно равен одному из следующих видов. При этом каждый из перечисленных видов (P,i)-спектра реализуется для некоторой полной теории T абелевых групп.
1) тождественно равен одному из следующих значений: 2ω, ω и n, где n < ω, n > 0;
2) тождественно равен одному из следующих значений: 2ω, ω, 2, 1;
3) либо максимальный, либо тождественно равен одному из следующих значений: 2ω, ω, n, где n < ω, n > 0;
4) либо максимальный, либо тождественно равен одному из следующих значений: ω и n, где n < ω, n > 0.
Е. А. Палютин P-спектры абелевых групп, Алгебра и логика, т. 53, N 2(2014), с. 216-255.
5. Изучена алгоритмическая сигма-размерность вещественного порядка в наследственно-конечной надстройке над вещественными числами.
Рассматриваемая в работе наследственно-конечная надстройка может служить атематической формализацией системы программирования с точной реализацией вещественных чисел. Эта ситуация имеет полное право на рассмотрение в связи с существованием аналоговых вычислительных устройств и последними работами по программным реализациям алгебраических чисел. В рамках одного из существующих подходов к программированию, реализации алгоритма предшествует эффективная реализация базовых структур данных, над которыми впоследствии будет разворачиваться его действие. Поэтому представляет интерес как изучение принципиальной возможности программной реализации различных алгебраических структур так и возникающих при этом специфических эффектов, в частности, определение числа попарно эффективно неизоморфных реализаций структур. Доказано, что класс возможных сигма-представлений для структуры порядка на вещественных числах в определенной мере необозрим: если разрешить использование произвольных параметров, то имеется несчётное число попарно не сигма-изоморфных (но классически изоморфных) представлений, а в случае, когда параметры фиксированы, класс таких представлений не может быть перечислен с теми же самыми параметрами. Построены также представления с некоторыми дополнительными свойствами.
Морозов А. С. Сигма-жёсткие представления вещественного порядка // Сибирский математический журнал, - Т. 55. - 2014. - вып. 3, - С. 562-572
Морозов А. С. О сигма-представлениях вещественного порядка // Алгебра и логика, - 2014. - Т. 53. - вып. 3
6. Доказана формула площади для липшицевых относительно субримановых метрик отображений пространств Карно – Каратеодори
В решении многих прикладных задач вычисление площади поверхностей имеет ключевое значение. До недавнего времени возможность посчета существовала только для ограниченного класса поверхностей: параметризованных отображениями со сравнимыми расстояниями между образами и между прообразами. Структуры неголономной геометрии возникают в теории субэллиптических уравнений, геометрической теории управления, физике, астродинамике, нейробиологии и др., но на этих структурах существует важный класс отображений, расстояние между образами которых может быть несравнимо больше расстояния между прообразами, например, если поверхность имеет фрактальную структуру.
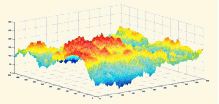
Остававшийся долгое время открытым вопрос о подсчете площади при таких параметризациях решен в работе [1]. Метод доказательства является новым и для отображений евклидовых пространств. У результата и метода уже есть успешные применения в трудной и актуальной проблеме описания минимальных поверхностей на группах Карно.
Карманова М. Б. Формула площади для липшицевых отображений пространств Карно - Каратеодори // Изв. РАН. Сер. мат. 2014. Т. 78, № 3. С. 53–78.
7. Получено обобщение теоремы Каратеодори для квазиконформных отображений.
Классическая теорема Каратеодори (1937) утверждает, что любое взаимно однозначное отображение расширенной комплексной плоскости, которое переводит окружности в окружности, является дробно-линейным или конформным. В данной работе получено обобщение теоремы Каратеодори для квазиконформных отображений. Установлено, что если отображение переводит окружности в k-квазиокружности, то оно K-квазиконформно, где K ≤ k+(k2-1)½.
Асеев В. В. «Квазиконформный аналог критерия Каратеодори мëбиусовости отображений» // Сиб. матем. журн., 2014, Т. 55, №1, С. 3-10.
8. Найдены точные константы в теореме Ball-Box.
Теорема Ball-Box была доказана Найджелом, Стейном и Вайнгером 1985 г. в связи с получениями оценок для некоторых субэллиптических операторов, например, таких, как X12+...+Xk2, где векторные поля X1,.., Xk удовлетворяют условию Хермандера. В теории субэллиптических уравнений огромную роль играет так называемая метрика Карно-Каратеодори, которая в нашем случае есть точная нижняя грань длин абсолютно непрерывных кривых таких, что их касательный вектор почти всюду принадлежит касательному подпространству, порожденному векторными полям X1,.., Xk (горизонтальные кривые). Однако, метрика Карно-Каратеоди, в силу своего сложного устройства практически непригодна для получения оценок. Теорема Ball-Box решает вопрос о нахождении билипшицево эквивалентной метрике Карно-Каратеодори квазиметрики (метрической функции, где аксиомы симметрии и неравенства треугольника понимаются в обобщенном смысле), удобной в практическом применении. Широкое применение квазиметрики было представлено в известной работе Кораньи и Рейманна «Основы теории квазиконформных отображений на группах Гейзенберга» (1995). Группалгебры H(n,α) являются естественным обобщением групп Гейзенберга, рассмотренных Кораньи и Рейманном (соответствует ситуации, когда α=−4); они (даже в более общем варианте) изучались в недавней работе Аграчева, Барилари и Боскаина «On the Hausdorff volume in sub-Riemannian geometry» (2012) в связи с вопросами геометрическое теории меры в субримановой геометрии.
Известная теорема Рашевского-Чоу гарантирует нам возможность соединения двух произвольных точек субриманова многообразия горизонтальной кривой, однако вычисление длины такой кривой, а тем более длины кратчайшей горизонтальной кривой сопряжена со значительными трудностями. Точные константы в теореме Ball-Box дают возможность альтернативного получения точных оценок в тех или иных вопросах современного геометрического анализа. Кроме того, точные константы в теореме Ball-Box являются своеобразной геометрической характеристикой сфер в метрике Карно-Каратеодори, устройство которых достаточно хорошо изучено лишь в одномерных группах Гейзенберга.
Новизна полученного результата. Задача о получении точных констант в теореме Ball-Box ранее никем не рассматривалась. Кроме того, исследовано поведение в зависимости от параметра α точных констант в теореме Ball-Box, а также сфер в метрике Карно-Каратеодори на H(n,α) . С первого взгляда может показаться, что метрическая геометрия на H(n,α) не зависит от выбора параметра α, однако нами построен пример (подобные примеры доселе также нигде не отмечались), показывающий, что при разных параметрах α соответствующие метрики Карно-Каратеодори не билипшицево эквивалентны.
Подходы и методы. Методы исследования, с одной стороны, базируются на классическом вариационном исчислении, с другой стороны, существенно используют технику вычисления в квазиметриках, что является оригинальным в данных вопросах.
Перспективы дальнейших исследований. В последнее время в субримановой геометрии и оптимальном активно решается задача об отыскании точного вида кратчайших в метрике Карно-Каратеодори на нильпотентных группах малой размерности или малой глубины (Аграчев, Сачков, Ардентов, Берестовский, Зубарева, Тайманов, Моховиков, Боскаин, Росси). Развитые нами подходы дают возможность для рассмотрения задачи о точных константах в теореме Ball-Box на таких объектах, как SO(3), SO(2,1), различных неголономных сублоренцевых обобщениях.
Грешнов А. В. Геометрия cc-шаров и константы в теореме Ball-Box на группалгебрах Гейзенберга// СМЖ. 2014. Т.55,
№ 5. С. 1040−1058
9. Получены качественные оценки локальной геометрии весовых квазиметрических пространств Карно—Каратеодори в окрестности нерегулярной точки.
Неголономные системы естественным образом возникают в задачах управления транспортными и космическими системами, термодинамики, нейробиологии, робототехники, квантовой механики и т. д. как системы с ограничениями (некоторые направления движения являются “запрещенными”, но при этом они связаны с “разрешенными” направлениями посредством коммутирования). Такие системы моделируются геометрией пространств Карно—Каратеодори, которая в рассматриваемой нами и практически важной ситуации ранее не была изучена. Полученные нами результаты важны для поиска оптимальных траекторий движения в перечисленных выше прикладных областях. 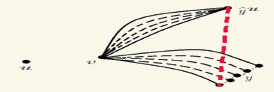
Рис. 1. Получена оценка максимального расхождения реальных траекторий в неголономной системе и их «нильпотентных аппроксимаций» (аналог линейных приближений), связанных с заданной точкой u при движении из некоторой близкой точки v. В отличие от стандартного случая, оцениваемых траекторий может быть бесконечное число.
Selivanova S. Metric Geometry of Nonregular Weighted Carnot–Carathéodory Spaces // Journal of Dynamical and Control Systems. 2014. V. 20, № 1. P. 123-148.
10. Получены асимптотически точные оценки скоростей сходимости в эргодических теоремах фон Неймана и Биркгофа для некоторых классических бильярдов и систем Аносова.
Даны новые оценки скорости сходимости в эргодической теореме Биркгофа. Получены асимптотически точные оценки скоростей сходимости в эргодических теоремах фон Неймана и Биркгофа для некоторых классических бильярдов и систем Аносова, по известным свойствам этих динамических систем: в теореме фон Неймана - через убывание корреляций (т.е. коэффициентов Фурье спектральной меры); в эргодической теореме Биркгофа - через убывание больших уклонений.
Качуровский А. Г., Подвигин И. В. Скорости сходимости в эргодических теоремах для некоторых бильярдов и систем Аносова // Докл. РАН. 2013. Т. 451, № 1. С. 11-13.
Качуровский А. Г., Подвигин И. В. Большие уклонения и скорости сходимости в эргодической теореме Биркгофа // Мат. заметки. 2013. Т. 94, № 4. С. 569-577.
Качуровский А. Г., Подвигин И. В. Скорости сходимости в эргодических теоремах для периодического газа Лоренца на плоскости // Докл. РАН. 2014. Т. 455, № 1. С. 11-14.
Подвигин И. В. Об экспоненциальной скорости сходимости в эргодической теореме Биркгофа // Мат. заметки. 2014.
Т. 95, № 4. С. 638-640.
Качуровский А. Г., Подвигин И. В. Оценки скоростей сходимости в эргодических теоремах фон Неймана и Биркгофа // Труды Московского мат. общества. 2015. Т. 76, № 1. 60 с. (принято к печати).
11. Построена дискретная вычислительная модель образования волн при сварке взрывом.
В 60 – х годах прошлого столетия академиком М.А. Лаврентьевым была поставлена проблема объяснение явления образования волн при косом соударении пластин, которые разгоняются скользящей детонационной волной. Несмотря на большое число работ, посвященных этой проблеме, она не поддавалась решению. Данным авторским коллективом эта проблема исследовалась экспериментально и теоретически методами численного моделирования на уровне сплошной среды и методом молекулярной динамики, в результате чего был предложен механизм образования волн на контактной границе при косом соударении пластин [1, 2]. В настоящее время сварка взрывом используется для изготовления высокопрочных композитных материалов. Результаты численных расчетов и эксперимента по развитию волн на контактной границе показаны на рисунке.

Рис. 1. а – численный расчет соударения алюминиевых пластин по схеме Годунова в упругопластической модели;
б - расчет соударения алюминиевых пластин методом молекулярной динамики; в – рентгеновский снимок соударения алюминиевой и свинцовой пластин (эксперимент).
Годунов С. К., Киселев С. П., Куликов И. М., Мали В. И. Численное и экспериментальное моделирование образования волн при сварке взрывом // Труды Математического Института им. В. А. Стеклова. 2013. Т. 281, С. 16 – 31.
Годунов С. К., Киселев С. П., Куликов И. М., Мали В. И. Моделирование ударно – волновых процессов в упругопластических материалах на различных (атомный, мезо и термодинамический) структурных уровнях.
– М. – Ижевск: Ижевский институт компьютерных исследований. 2014. – 296 с.
12. Выведены основные уравнения магнито-фотоупругости для общего случая неоднородной изотропной референтной среды и для переменного внешнего магнитного поля. Выполнена линеаризация этих уравнений относительно переменных коэффициентов, и найдено явное аналитическое решение линеаризованных уравнений.
Закаленное стекло широко применяется в современной промышленности: автомобильные стекла, стеклянные панели в строительстве и многое другое. Правильно закаленное стекло на порядок прочнее по отношению к вибрационным и ударным нагрузкам, чем то же стекло до закаливания. Закаливание стеклянной пластины состоит в основном в создании так называемых остаточных напряжений внутри стекла; причем эти напряжения должны быть неравномерно распределены по толщине пластины: растягивающие напряжения в средней части пластины и сжимающие напряжения вблизи граничных плоскостей. Для создания таких напряжений используется довольно сложная технология термической обработки, состоящая из медленного нагревания и быстрого охлаждения, причем для получения нужного профиля остаточных напряжений этот процесс нагревания и охлаждения повторяется несколько раз в разных режимах. Нарушения этой технологии зачастую приводят к противоположному результату: неправильно закаленная пластина оказывается более хрупкой, чем та же пластина до закаливания.
Современная стекольная промышленность остро нуждается в средствах контроля процесса закаливания: требуется определить распределение остаточных напряжений в закаленной стеклянной пластине с целью контроля двух основных характеристик: (1) равномерности распределения напряжений по площади пластины и (2) правильности профиля напряжений по толщине пластины. Для первой задачи используется классический метод фотоупругости, состоящий в просвечивании пластины монохроматическим поляризованным светом и измерении параметров поляризации прошедшей электромагнитной волны. В частности, в случае постоянства напряжений по толщине пластины, известный закон Вертгейма позволяет выразить две компоненты тензора напряжений через измеренные параметры поляризации. Если же напряжения меняются по толщине пластины, то измерение поляризации прошедшей волны дает лишь среднее арифметическое значение искомого профиля. Поэтому классическая фотоупругость недостаточна для решения второй задачи. Используя квазиизотропное приближение геометрической оптики,
В. А. Шарафутдиновым выведены основные уравнения магнито-фотоупругости для общего случая неоднородной изотропной референтной среды и для переменного внешнего магнитного поля. Выполнена линеаризация этих уравнений относительно переменных коэффициентов, отвечающих за оптическую анизотропию, вызванную тензором напряжений и найдено явное аналитическое решение линеаризованных уравнений, которое тривиализует обратную задачу для (2). Результаты поляризационных измерений позволяют получить коэффициенты Фурье искомого профиля, что также решает проблему необходимой точности измерений и требуемого их количества, сводя эти вопросы к хорошо изученным свойствам рядов Фурье.
Vladimir Sharafutdinov The linearized problem of magneto-photoelasticity. Inverse Problems and Imaging. Vol. 8, No. 1. 2014, 247-257. doi:10.3934/ipi.2014.8.247
13. Получены формулы конструктивного построения решений и коэффициентов дифференциальных уравнений с практической целью предсказательного моделирования волновых, тепловых и других процессов.
В работах авторов приведены новые представления решений и коэффициентов уравнений математической физики, которые являются дифференциально-алгебраическими тождествами. Полученные представления частично использованы при изучении многомерных и одномерных обратных задач.
Для общих эволюционных уравнений, содержащих переменный параметр, сформулированы результаты представления решений и функций источников, зависящих не только от пространственной переменной, но и от времени, найдены формулы для решений обратных задач типа управления. При этом следует подчеркнуть, что получение зависимости данных обратных задач от параметра связано с дополнительными измерениями. С другой стороны, появляется возможность прогнозирования, так как при наличии переменного параметра находятся не факторизованные, а общие коэффициенты и функции источников, зависящие от пространственной переменной и времени.
Приведены новые представления решений и коэффициентов эволюционных дифференциальных уравнений 2-го порядка в линейном и нелинейном случаях. Получены новые тождества и представления, связанные с преобразованием Хопфа-Коула. Найденные авторами формулы для линейных уравнений содержат значительный произвол, что может быть использовано в задачах идентификации.
Кроме того, исследован ряд конкретных уравнений математической физики. Так для волнового уравнения в пространстве произвольной размерности доказано, что 1) формула Смирнова-Соболева дает все вещественнозначные функционально инвариантные решения, 2) многофазные решения являются существенно комплекснозначными. Рассмотрена задача построения амплитуд обобщенных функционально инвариантных решений по заданной фазе. Решена задача описания амплитуд обобщенных функционально инвариантных решений волнового уравнения для фазовых функций типа сферической волны. Для нелинейных одномерных уравнений изучаются вопросы типа бегущей волны.
1. Anikonov Yu. E., Neshchadim M. V. Representations for the solutions and coefficients of second-order differential equations. Journal of Applied and Industrial Mathematics. V. 7, N 1(2013), p. 1–7.
2. Anikonov Yu. E., Neshchadim M. V. Representations for the solutions and coefficients of evolution equations. Journal of Applied and Industrial Mathematics. V. 7, N 3(2013), p. 326 –334.
3. Нещадим М. В. Классы обобщенных функционально инвариантных решений волнового уравнения. I. Сибирские электронные математические известия. Т. 10(2013), с. 418 – 435. http://semr.math.nsc.ru
4. Anikonov Yu. E., Neshchadim M. V. Analytical methods of the theory of inverse problems for parabolic equations. Journal of Mathematical Sciences. December 28, 2013, Volume 195, Issue 6, pp. 754 – 770.
5. Нещадим М. В. Сферические обобщенные функционально инвариантные решения волнового уравнения. Вестник НГУ, сер. математика, механика, информатика. Т. 14, N 2(2014), с. 42-48.
6. Нещадим М. В. Интегральная средняя кривизна и бесконечно малые изгибания поверхностей в 3-х мерном римановом пространстве. СМЖ. Т. 55, N 5(2014), с. 1167 – 1174.
7. Аниконов Ю. Е. Дифференциальные тождества для уравнений с частными производными. Сибирский журнал индустриальной математики. Т. 17, N 2(2014), 11 – 17.
8. Аниконов Ю. Е., Аюпова Н. Б. Преобразование Хопфа-Коула и многомерные представления решений эволюционных уравнений, Сибирский журнал индустриальной математики. Т. 17, N 4(2014), 31 – 37.
14. Получены формулы для восстановления оператора свертки на полупрямой.
Исследуется интегральное уравнение Вольтерра первого рода в свертках на полупрямой при достаточно естественных предположениях о ядре и правой части уравнения (ядро интегрального оператора имеет ограниченный носитель). В этом случае впервые поставлена и решена обратная задача по восстановлению решения уравнения и ядра интегрального оператора по значениям правой части уравнения. В работе получены необходимые и достаточные условия разрешимости поставленной обратной задачи, доказана теорема единственности, получены явные формулы для восстановления решения и ядра.
Результаты работы могут найти применения в геофизике, при обработке сейсмических измерений, в частности, на стадии создания измерительных приборов, а также в теории сигналов.
А. Ф. Воронин Восстановление оператора свертки по правой части на вещественной полуоси. Сиб. журн. индустр. матем., 2014, 17:2, 32–40
15. Установлены условия экспоненциальной устойчивости решений некоторых классов систем дифференциальных уравнений с запаздывающим аргументом нейтрального типа, получены оценки решений.
Проведены исследования устойчивости решений некоторых классов систем линейных дифференциальных уравнений с запаздывающим аргументом нейтрального типа. Рассмотрены классы уравнений с постоянными и периодическими коэффициентами при постоянных и переменных запаздываниях. Получены достаточные условия экспоненциальной устойчивости решений и изучена робастная устойчивость. Условия устойчивости формулируются в терминах матричных неравенств типа Ляпунова-Риккати. Установлены оценки решений, характеризующие скорость стабилизации на бесконечности, и указан диапазон возмущений коэффициентов дифференциальных уравнений, при которых сохраняется экспоненциальная устойчивость решений. При получении результатов использовались введенные ранее функционалы типа Ляпунова-Красовского и доказанные теоремы о разрешимости краевых задач для дифференциального уравнения Ляпунова.
Демиденко Г. В., Матвеева И. И. Об экспоненциальной устойчивости решений одного класса систем дифференциальных уравнений нейтрального типа // Сибирский журнал индустриальной математики. 2014. Т. 17, № 3.
Демиденко Г. В., Матвеева И. И. Об оценках решений систем дифференциальных уравнений нейтрального типа с периодическими коэффициентами // Сибирский математический журнал. 2014. Т. 55, № 5.
Demidenko G. V., Matveeva I. I. Estimates for solutions to linear systems of neutral type with several delays // Journal of Analysis and Applications. 2014. V. 12, No 1.
Скворцова М. А. Асимптотические свойства решений систем уравнений нейтрального типа с переменным запаздыванием // Вестник НГУ. Серия: Математика, механика, информатика. 2013. Т. 13, № 4.
16. Доказана локальная по времени теорема существования и единственности решения задачи со свободной границей плазма-вакуум в подходящих весовых анизотропных пространствах Соболева в предположении, что в начальный момент времени плотность плазмы строго положительна вплоть до границы, а магнитные поля в плазме и вакууме не коллинеарны в каждой точке свободной границы.
Задача со свободной границей плазма-вакуум рассмотрена в классической постановке, когда течение плазмы описывается гиперболическими уравнениями магнитной гидродинамики идеальной сжимаемой жидкости для вектора неизвестных U = (p,v,H,S), а магнитное поле в вакууме H подчиняется эллиптической системе предмаксвелловской динамики rot H = 0, div H = 0, где p = p(p, S) — давление, p — плотность плазмы, S — энтропия, v и H — векторы скорости и магнитного поля в плазме. Свободная граница Г(t) = { F(t, x) = 0} между плазмой и вакуумом движется со скоростью частиц плазмы на ней:
dF/dt = 0 на Г(t)
(для всех t € [0,T]), где d/dt = dt + (v-V). Остальные граничные условия требуют непрерывности полного давления
q = p+2 |H|2 и параллельности свободной границе магнитных полей со стороны плазмы и со стороны вакуума:
[q] = 0, H * N = 0, H * N = 0 на Г(t),
где N = V— — нормаль к Г, а [q] = q|r — 21H|2Г.
Задача со свободной границей плазма-вакуум используется для моделирования удержания плазмы магнитными полями, а в астрофизике при моделировании движения звезды (например, солнечной короны). Основные теоретические исследования этой задачи были связаны с огромной популярностью (особенно в 50-е-70-е годы XX века) вопроса удержания плазмы и посвящены нахождению критериев устойчивости состояний равновесия. Типичной работой в этом направле¬нии является классическая статья [I. B. Bernstein, E. A. Frieman, M. D. Kruskal, R. M. Kulsrud, Proc. Roy. Soc. A 244 (1958), 17-40]. До сих пор, однако, не было результатов о корректности полной (нестационарной) задачи со свободной границей плазма-вакуум.
В предположении, что в начальный момент времени плотность плазмы строго положительна вплоть до границы, а магнитные поля в плазме и вакууме не коллинеарны в каждой точке свободной границы, доказана локальная по времени теорема существования и единственности решения задачи со свободной границей плазма-вакуум в весовых анизотропных пространствах Соболева Hs.
Trakhinin Y. On the well-posedness of a linearized plasma-vacuum interface problem in ideal com-pressible MHD // Journal of Differential Equations. - 2010. - V. 249. - N. 10. - P. 2577-2599.
Secchi P., Trakhinin Y. Well-posedness of the linearized plasma-vacuum interface problem // Interfaces and Free Boundaries. - 2013. - V. 15. - N. 3. - P. 323-357.
Secchi P., Trakhinin Y. Well-posedness of the plasma-vacuum interface problem // Nonlinearity. - 2014. - V. 27. - N. 1. - P. 105-169.
17. Описана геометрия фазовых портретов нелинейных динамических систем химической кинетики малых размерностей. Построены инвариантные многообразия, содержащие периодические траектории.
Установлены достаточные условия, при которых нелинейная несимметричная динамическая система размерности 3, моделирующая функционирование молекулярного репрессилятора имеет в точности один цикл. Установлены условия неединственности циклов в фазовых портретах аналогичных нелинейных динамических систем размерностей 4 и 5. Описаны стационарные точки таких систем и дискретные схемы их фазовых портретов. Для размерности 4 описан конструктивный метод нахождения сепаратрисной гиперповерхности, разделяющей области притяжения устойчивых стационарных точек и содержащей цикл. Для всех описанных динамических систем описан конструктивный метод нахождения инвариантных поверхностей, содержащих их циклы.
Акиньшин А. А., Голубятников В. П., Голубятников И. В. О некоторых многомерных моделях функционирования генных сетей. Сиб. журнал индустриальной математики, 2013, том 16, N 1, с. 3 - 9
Ayupova N. B., Golubyatnikov V. P. On the uniqueness of a cycle in an asymmetric three-dimensional model of a molecular repressilator. Journal of applied and industrial mathematics, 2014, v. 17, N 1, p. 3 – 7.
18. Найдена аппроксимация второго порядка для распределения максимума случайного блуждания с отрицательным сносом и бесконечной дисперсией.
Задача о распределении максимума случайного блуждания с отрицательным сносом возникает при изучении вероятностей сбоев разного рода систем в таких прикладных областях как теория риска, теория коммуникационных систем и систем обслуживания, теория страхования и др. Аппроксимация первого порядка для малых вероятностей такого рода была найдена в 1972 г. и нашла широкое применение. Однако выяснилось, что она дает систематическую погрешность и не всегда является удовлетворительной. Поэтому стала востребованной задача об аппроксимации второго порядка. В случае существования дисперсии скачка блуждания такая аппроксимация была найдена автором в 2002 г. Случай, когда дисперсия не существует, не менее востребован, но он аналитически оказался более трудным. В предлагаемой работе эта задача при широких условиях решена.
А. А. Боровков Аппроксимация второго порядка для распределения максимума случайного блуждания с отрицательным сносом и бесконечной дисперсией // Теория вероятностей и ее применения. 2014. Т. 59, №1. С. 5 – 24.
19. Завершен цикл работ, связанных с получением оценок и предельных теорем для максимальной длины пути в различных классах направленных ациклических случайных графов. Доказан ряд эргодических и функциональных предельных теорем. Развита теория условных регенерирующих случайных процессов.
Ациклические случайные графы возникают в различных прикладных моделях: коммуникационных сетях и системах обслуживания, биологических системах и т.д. Первые такие модели были предложены Е. Гелембе (1989-90) для описания систем и сетей обслуживания со случайными зависимостями. Модели со случайными ребрами фиксированной длины и связанные с ними биологические модели были рассмотрены в цикле работ Ч. Ньюмана с соавторами (1991-97), авторами были доказаны предельные теоремы пуассоновского типа в схеме серий. В работах С. Г. Фосса с соавторами рассматривается другой тип предельного перехода: вероятности существования ребер фиксируются, как и распределения их длин, а число ребер устремляется к бесконечности. Доказано, что если распределение случайной длины типичного ребра имеет конечный второй момент, то структура графов является условно регенерирующей и предельные процессы являются функционалами от броуновских движений; если же второй момент бесконечен, то предельные процессы оказываются совсем иными. Попутно развита теория регенерирующих случайных процессов, зависящих от бесконечного будущего. Это позволило также получить качественно новые результаты в теории контактных процессов. Показана тесная связь рассматриваемых вопросов с известной проблемой last-passage percolation в размерностях один и два, а также с т.н. процессами с «долгой памятью» (processes with long memory) и проблемами точного моделирования (perfect simulation) в них; с аналогичными проблемами в теории случайных матриц и в других направлениях.
[1]. S. Foss and T. Konstantopoulos. Extended renovation theory and limit theorems for stochastic ordered graphs. Markov Processes and Related Fields, 9 (3), 2003, 413—468.
[2]. D. Denisov, S. Foss, and T. Konstantopoulos. Limit theorems for a random directed slab graph. The Annals of Applied Probability, 22 (2), 2012, 702—733.
[3]. S. Foss and S. Zachary. Stochastic sequences with aregenerative structure that may depend both on the future and on the past. Advances in Applied Probability, 45 (4), 2013, 1083—1110.
[4]. S. Foss, J. Martin, P. Schmidt. Long-range last-passage percolation on the line. The Annals of Applied Probability, 24 (1), 2014 198—234
20. Изучены аппроксимационные свойства интерполяционных сплайнов четной степени двух конструкций (по Субботину и по Марсдену), установлена связь между условиями сходимости процессов интерполяции этих конструкций.
Исследованы две принципиально различные конструкции интерполяционных сплайнов
четной степени 2m (по Субботину и по Марсдену). Отличие между этими конструкциями заключается в том, что для сплайна по Субботину задаются узлы интерполяции, а узлы сплайны (точки склейки звеньев сплайна) выбираются посредине между узлами интерполяции. Наоборот, для конструкции сплайна по Марсдену задаются узлы сплайна, а узлы интерполяции выбираются между ними. На основе разработанного ранее автором подхода к построению полиномиальных сплайнов впервые получены системы для параметров сплайнов произвольной четной степени 2m обеих конструкций. Доказаны теоремы о погрешности приближения интерполируемой функции и ее производных. Полученные результаты показывают, что хотя интерполяционные сплайны по Марсдену и по Субботину – это две совершенно разные конструкции, вопросы сходимости таких сплайнов тесно связаны между собой. В частности, условия сходимости k-й производной для сплайна степени 2m по Марсдену и (2m-k)-производной сплайна по Субботину будут одинаковыми при интерполировании функций с соответствующими минимальными требованиями к гладкости.
Волков Ю. С. Интерполяция сплайнами четной степени по Субботину и Марсдену // Украïнский математичний журнал. 2014. Т. 66, № 7. С. 891-908.
21. Показана линейная асимптотическая неустойчивость стационарного течения полимерной среды в плоском канале в случае периодических возмущений.
Изучается новая реологическая модель, описывающая течения реальных растворов и расплавов линейных полимеров различных молекулярных масс и концетраций в областях со сложной геометрией. Предложенная модель - обобщение известной модели Покровского - Виноградова - ввиду нового реологического соотношения учитывает тонкие особенности, которые необходимо учитывать при создании новых технологий, например, появление второго вихря у кромки на входе в узкий канал, появление периодического и непериодического поведения потока при достижении некоторой критической скорости течения (т.е. нужных значений чисел Вайсенберга и Деборы).
В случае течения в бесконечном плоском канале (рис. 1) у модели существует экспериментально наблюдаемый аналог течения Пуазейля для системы уравнений Навье-Стокса (профили скорости при различных значениях физических параметров представлены на рис.2).
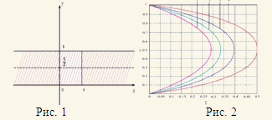 Для малых периодических по длине канала возмущений сформулирована и исследована линейная смешанная задача для нахождения компонент вектора скорости, тензора анизотропии второго ранга и давления. Доказано, что аналог течения Пуазейля не является асимптотически устойчивым по Ляпунову.
Для малых периодических по длине канала возмущений сформулирована и исследована линейная смешанная задача для нахождения компонент вектора скорости, тензора анизотропии второго ранга и давления. Доказано, что аналог течения Пуазейля не является асимптотически устойчивым по Ляпунову.
Таким образом, предложенная реологическая модель, дающая описание течений полимеров, требует существенной коррекции.
Блохин А. М., Ткачев Д. Л. Линейная асимптотическая неустойчивость стационарного течения, полимерной среды, в плоском, канале в случае периодических возмущений // Сиб. журн. индустр. матем., 2014, Т. 17, №3. С. 13-25.
22. Исследованы свойства решений задачи Коши для систем интегро-дифференциальных и разностных уравнений, описывающих в новой постановке процесс распространения и контроля туберкулеза в регионах России.
Разработана и исследована новая версия математической модели распространения и контроля туберкулеза в отдельно взятых регионах России. Уравнения модели построены с учетом воспроизводства населения региона и импульсного изменения численностей групп индивидуумов под влиянием различных факторов. Найдены решения модели, соответствующие полному искоренению туберкулеза в регионе. Получены решения модели, обосновывающие возможность поддержания численностей групп инфицированных и больных индивидуумов в регионе на заданном допустимом уровне.
Перцев Н. В. Непрерывно-дискретная модель распространения и контроля туберкулеза // Сибирский журнал индустриальной математики. 2014. Т.XVII. №3. С. 86-97.
Pertsev N. V., Leonenko V. N. Analysis of stochastic model for the spread of tuberculosis with regard to reproduction and seasonal immigration of individuals // RJNAMM. 2014. V.29. №5. P.285-295.
23. Поставлена и исследована задача радиационного зондирования среды, когда используется всего одно или два направления (ракурса) излучения.
Известными данными считаются результаты измерения плотности радиационного потока, прошедшего через среду. Целью работы является получение информации о внутреннем строении обследуемого объекта. Исследование выполнено Аниконовым Д.С. совместно с его учениками, и его выводы опубликованы в четырех статьях, последняя из которых: Аниконов Д.С., Назаров В.Г., Прохоров И. В. Интегро-дифференциальный индикатор для задачи одноракурсной томографии // Сибирский журнал индустриальной математики, 2014. Т. 17, №2(58). С. 3-10.
Кроме того, получен патент на изобретение и три свидетельства о госрегистрации соответствующих программ.
Ниже приведена реконструкция границ двух шарообразных включений в среде, зондируемой очень слабым рентгеновским излучением. Слева показана реконструкция, основанная на непосредственном измерении потока фотонов (фотография). На изображении справа дана реконструкция, основанная на одном из алгоритмов, предложенных авторами. Другие численные эксперименты также подтверждают соответствие предложенных алгоритмов поставленной задаче.
 Достигнутые результаты могут быть использованы для создания локатора нового типа, когда в качестве зондирующего сигнала используется естественная радиация окружающей среды.
Достигнутые результаты могут быть использованы для создания локатора нового типа, когда в качестве зондирующего сигнала используется естественная радиация окружающей среды.
1. Аниконов Д. С., Прохоров И. В., Назаров В. Г., Солнышко Н. В. Способ маскировки изделий. //Патент Российской Федерации № 2264424. Бюллетень № 32, 20.11.2005, заявка № 2003124026 от 30.07.2003 г.
2. Аниконов Д. С., Ковтанюк А. Е., Назаров В. Г., Прохоров И. В., Суровенко Н. С., Яровенко И. П. База данных радиационных характеристик веществ, представляющих интерес в рентгенодиагностике. // Свидетельство о государственной регистрации базы данных № 2009620348, зарегистрировано в Реестре баз данных 19.06.2009. Опубликовано в официальном бюллетене «Программы для ЭВМ, базы данных, топологии интегральных микросхем». 2009. № 3. С. 334-335.
3. Аниконов Д. С., Ковтанюк А. Е., Назаров В. Г., Прохоров И. В., Суровенко Н. С., Яровенко И. П. Определение контраста неоднородной среды в рентгеновской томографии. //Свидетельство о государственной регистрации программ для ЭВМ № 2009613135, Зарегистрировано в Реестре программ для ЭВМ 16.06.2009. Опубликовано в официальном бюллетене «Программы для ЭВМ, базы данных, топологии интегральных микросхем». 2009. С. 479-480.
4. Аниконов Д. С., Назаров В. Г. Улучшение качества двумерных изображений в задачах одноракурсной томографии
// Свидетельство о государственной регистрации программы для ЭВМ № 2012618709. Зарегистрировано в Реестре программ для ЭВМ 30 июля 2012 года, бюллютень №4
5. Anikonov D. S., Nazarov V. G. & Prokhorov I. V. Algorithm of finding a body projection within an absorbing and scattering medium. Journal Inverse and Ill-Posed Problems. 2011, V. 19, № 2, P.11-19.
6. Аниконов Д. С., Назаров В. Г., Прохоров И. В. Задача одноракурсного зондирования неизвестной среды. Сибирский журнал индустриальной математики. 2011, Т. 14, № 2(46), С. 9-16.
7. Аниконов Д. С., Назаров В. Г. Задача двуракурсной томографии // ЖВМиМФ, 2012. 52,№ 3, стр. 372-378.
8. Аниконов Д. С., Назаров В. Г., Прохоров И. В. Интегро-дифференциальный индикатор для задачи одноракурсной томографии // Сибирский журнал индустриальной математики, 2014. Т. 17, №2(58). С. 3-10.
24. Дано полное описание элементов ядра вполне положительной кооперативной игры, согласованных с иерархией ее участников. Ключевую роль в характеризации этих элементов играет развитый автором структурный подход, опирающийся на методы теории векторных решеток.
Аксиоматизирован принцип оптимальности теории кооперативных игр, сопоставляющий каждой вполне положительной игре v совокупность CГ(v) элементов классического ядра C(v), согласованных с иерархией Г. При этом иерархия Г определяется некоторым отношением подчиненности между игроками, а под согласованностью дележа (u1,...,un) с этой иерархией понимается выполнение, среди прочих, следующего условия: ui ≥ uj для любого игрока j, подчиненного i в Г. Используя развитый автором структурный подход [1,2], опирающийся на методы теории полуупорядоченных векторных пространств, удается получить полное описание многозначного отображения v → CГ(v), v  V+, в основном, в терминах частичного порядка, порожденного конусом V+. Определяющим обстоятельством при этом оказывается дизъюнктная аддитивность соответствующего отображения Харшаньи [1]. Среди других аксиом, дающих описание ограниченного ядра CГ(v), следует отметить аксиому структурной монотонности, формализующую упоминавшуюся уже согласованность дележей из CГ(v) с иерархией Г. V+, в основном, в терминах частичного порядка, порожденного конусом V+. Определяющим обстоятельством при этом оказывается дизъюнктная аддитивность соответствующего отображения Харшаньи [1]. Среди других аксиом, дающих описание ограниченного ядра CГ(v), следует отметить аксиому структурной монотонности, формализующую упоминавшуюся уже согласованность дележей из CГ(v) с иерархией Г.
Полученные теоретико-игровые результаты нацелены на анализ ряда актуальных проблем водопользования:
1) рациональное распределение индивидуальных издержек на строительство совместных очистных сооружений,
2) выбор эффективного объема водопотребления вдоль речных сетей (с учетом естественных линейных иерархий потребителей) и т.п. В частности, показано, что построенная общая аксиоматизация ограниченного (иерархического) ядра дает исчерпывающее описание этих ядер и для так называемых DR-игр. Последние особенно интересны тем, что помимо экологических, моделируют и ряд других важных задач коллективного выбора [3].
1. Vasil’ev V. A., van der Laan G. The Harsanyi set for cooperative TU-games // Siberian Adv. Math, (2002), 12, p,97-125.
2. Vasil’ev V. A. Cores and generalized NM-solutions for some classes of cooperative games // In: Russian Contributions to Game Theory and Equilibrium Theory (eds. T. Driessen, G. van der Laan, V. Vasil’ev, and E. Yanovskaya), Berlin-New York: Springer Verlag (2006), p. 91-150.
3. R. van den Brink, G. van der Laan, V. Vasil’ev Constrained core solutions for totally positive games with ordered players
// Int. J. Game Theory (2014), 43, p.351-368.
25. Исследованы модели экономики с выпуклым и невыпуклым производством с помощью оригинального договорного подхода, представляющего новую модель совершенной конкуренции. Доказан ряд теорем об эквивалентности равновесий и договорных распределений разного типа с частичным разрывом договоров, в следствии чего было обосновано важное понятие равновесия по предельным затратам.
Исследуются модели экономики с выпуклым и невыпуклым производством с помощью оригинального договорного подхода. Понятийная база теории договоров модифицируется и адаптируется к моделям этого типа: уточняются понятия сети договоров, доминирования сетей по коалициям, частичный разрыв договоров и др. Для модели с невыпуклым производством введено новое понятие маргинально договорного распределения, которое затем используется в анализе равновесия с ценообразованием по предельным затратам (MCP-равновесие). Основные результаты представлены в ряде теорем об эквивалентности равновесий и договорных распределений разного типа с частичным разрывом договоров. В частности, доказана эквивалентность между MCP-равновесием и маргинально договорными распределениями, что можно рассматривать как теоретическое обоснование концепции MCP-равновесия в невыпуклых экономиках. В целом работа развивает договорной подход как универсальный метод моделирования условий совершенной конкуренции.
Маракулин В. М. О договорном подходе в моделях экономики типа Эрроу - Дебре -Маккензи // Экономика и Математические Методы, 2014. Том 50, № 1, с. 61—79
26. Получены новые нижние оценки на число ребер в критических по раскраске графах. В частности, доказана известная гипотеза Галлаи (1963 года) на эту тему и асимптотически доказана гипотеза Оре (1967 года).
k-Раскраской графа называется функция f, сопоставляющая каждой вершине графа число от 1 до k так что смежные вершины получают разные цвета. Граф называется k-критическим, если он не допускает (k-1)-раскраски, но каждый его подграф допускает. Знание структуры k-критических графов важно для понимания природы раскрасок. Получены новые нижние оценки на минимально возможное число ребер в k-критических графах с n вершинами. В частности, доказана соответствующая гипотеза Галлаи 1963 года и асимптотически доказана Гипотеза Оре 1967 года.
Используя эти оценки, получены новые результаты о раскраске плоских графов, особенно о 3-раскраске. В частности, описаны все 4-критические плоские графы с ровно 4 треугольниками. Тем самым отвечено на вопрос Аксенова 1978 года и Эрдеша 1991 года. Эти результаты уже используются другими математиками.
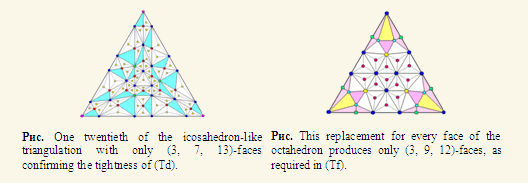
Kostochka, Alexandr; Yancey, Matthew; Ore's conjecture on color-critical graphs is almost true. J. Combin. Theory Ser. B 109 (2014), 73–101.
Borodin, Oleg V.; Dvorak, Zdenek; Kostochka, Alexandr V.; Lidicky, Bernard; Yancey, Matthew; Planar 4-critical graphs with four triangles. European J. Combin. 41 (2014), 138–151.
Kostochka, Alexandr; Yancey, Matthew; Ore's conjecture for k=4 and Grotzsch's theorem. Combinatorica 34 (2014), no. 3, 323–329.
Borodin, Oleg V.; Kostochka, Alexandr V.; Lidicky, Bernard; Yancey, Matthew; Short proofs of coloring theorems on planar graphs. European J. Combin. 36 (2014), 314–321.
Kostochka, Alexandr; Yancey, Matthew; On coloring of sparse graphs. Computer science — theory and applications, 224–234, Lecture Notes in Comput. Sci., 7913, Springer, Heidelberg, 2013.
27. Доказано, что задача поиска разреза максимального веса в полном неориентированном графе, вершинами которого являются точки q-мерного пространства, относится к числу NP-трудных в сильном смысле задач и для неё не существует полностью полиномиальной приближенной схемы (FPTAS) в случаях, когда длины рёбер равны евклидовым расстояниям между точками пространства и квадратам этих расстояний, если P≠NP.
Задача Max-Cut (максимальный разрез) известна под номером 21 в списке классических NP–полных задач (Karp, 1972). Вопрос о статусе сложности евклидового случая задачи, когда вершинами являются точки q-мерного пространства, поднимался в литературе в 90-е годы, но оставался открытым. Доказано, что задача NP-трудна в сильном смысле, когда длины ребер равны: 1) евклидовым расстояниям между точками пространства, 2) квадратам этих расстояний. Из полученных результатов следует, что для этих случаев задачи не существует ни точных полиномиальных алгоритмов, ни точных псевдополиномиальных алгоритмов (в предположении, что гипотеза P≠NP верна). Показано также, что для них не существует полностью полиномиальной приближенной схемы (FPTAS), если P≠NP.
Агеев А. А., Кельманов А. В., Пяткин А. В. Труднорешаемость задачи о разрезе максимального веса в евклидовом пространстве // Доклады РАН. 2014. Т. 456, №5. С. 511-513.
Агеев А. А., Кельманов А. В., Пяткин А. В. Cложность задачи о разрезе максимального веса в евклидовом пространстве // Дискретный анализ и исследование операций, 2014. Т. 21, №4. С. 3-11.
28. Доказана NP-трудность оптимальной рекомбинации для задачи минимизации общего времени завершения работ на одной машине. Показана полиномиальная разрешимость «почти всех» индивидуальных задач оптимальной рекомбинации для данной задачи.
Работоспособность генетических алгоритмов существенно зависит от выбора оператора кроссинговера, где комбинируются элементы родительских решений при построении решений-потомков. Задача оптимальной рекомбинации (ЗОР) состоит в отыскании наилучшего возможного результата кроссинговера при заданных двух родительских решениях комбинаторной задачи оптимизации. В генетических алгоритмах для задач, где множество допустимых решений составляют перестановки, алгоритмы кроссинговера подобного типа применялись в работах
M. Yagiura и T. Ibaraki (1996), C. Cotta с соавт. (1998), W. Cook и P. Seymour (2003) и др.
Задача минимизации общего времени завершения работ на одной машине с произвольными длительностями переналадки, обозначаемая в теории расписаний 1|sij|Cmax, состоит в отыскании перестановки работ, при которой минимизируется суммарная длительность переналадок машины. Посредством сводимости NP-трудной задачи коммивояжера с предписаниями вершин доказана NP-трудность ЗОР для 1|sij|Cmax. Предложен алгоритм решения ЗОР для 1|sij|Cmax, основанный на переборе совершенных паросочетаний в специальном двудольном графе. Показано, что для «почти всех» пар родительских решений трудоемкость данного алгоритма полиномиально ограничена.
Новизна полученного результата состоит в том, что впервые для задачи оптимальной рекомбинации, труднорешаемой в общем случае (если верна гипотеза P≠NP), предложен эффективный алгоритм c полиномиальным временем работы для «почти всех» индивидуальных задач.
Решение задачи оптимальной рекомбинации в генетических алгоритмах позволяет во многих случаях получать более эффективные варианты генетических алгоритмов по сравнению с классическими. Задача минимизации общего времени завершения работ имеет приложения в машиностроении (покраска автомобилей различными красками), химической (производство пластмасс с различными свойствами), пищевой промышленности и др.
Еремеев А. В., Коваленко Ю. В. О сложности оптимальной рекомбинации для одной задачи составления расписаний с переналадками // Дискретный анализ и исследование операций. 2012. Т. 19, № 3, С. 13-26.
Еремеев А. В., Коваленко Ю. В. О сложности оптимальной рекомбинации для некоторых задач на перестановках
// Материалы Международной конференции "Интеллектуализация обработки информации", (16-22 сентября 2012 г. Будва, Черногория). - C. 245-248.
Eremeev A. V., Kovalenko J. V. Optimal recombination in genetic algorithms for combinatorial optimization problems: Part II
// Yugoslav Journal of Operations Research. 2014. Vol. 24. N 2, P. 165-186.
29. Доказана инвариантность межвесового спектра совершенных кодов и их обобщений – полностью регулярных кодов и совершенных раскрасок (регулярных разбиений). Выведены рекуррентные и прямые формулы для вычисления межвесового распределения по параметрам полностью регулярного кода или регулярного разбиения.
Инвариантность межвесового распределения регулярных разбиений и его вычисление.
Серия работ посвящена вычислению межвесовых распределений полностью регулярных кодов и регулярных разбиений (также известных как совершенные раскраски) по их параметрам.
История вопроса. В знаменитой статье “On the Mathematical Theory of Error-Correcting Codes” 1959г Х.С.Шапиро и Д.Л.Злотник доказывают дистанционную инвариантность совершенных кодов: весовой спектр такого кода, то есть распределение расстояний вершин кода до фиксированной кодовой вершины, зависит только от параметров кода (мы будем рассматривать только двоичные коды, то есть подмножества множества вершин гиперкуба). На основе этой теоремы они делают ошибочное предположение, что совершенный код, исправляющий одну ошибку, единственный для каждой допустимой длины – код Хэмминга. Вскоре, в 1962г., эта гипотеза опровергается Ю.Л.Васильевым, который строит дважды экспоненциальное относительно длины число неэквивалентных 1-совершенных кодов. И согласно теореме Шапиро и Злотника, все эти коды имеют один и тот же весовой спектр. В первой статье [1] цикла доказывается еще более удивительный факт: не только весовое, но и межвесовое распределение всех двоичных 1-совершенных кодов одной длины одинаково. Под межвесовым распределением подразумевается число пар кодовых вершин (Y,Z) с данными расстояниями d(X,Y), d(X,Z) и d(Y,Z) от фиксированной вершины X и между собой. Во второй статье [2] результат обобщается на значительно более широкий класс объектов – совершенные раскраски и полностью регулярные коды. В завершающей статье [3] цикла выводятся формулы для вычисления межвесового распределения совершенных раскрасок, в том числе полностью регулярных кодов. Предложены как рекуррентные, так и прямые формулы, последние используют новое обобщение многочленов Кравчука на многочлены от трех переменных. Инвариантность межвесового распределения и формулы его вычисления уже находят применение для доказательства несуществования полностью регулярных кодов с конкретными параметрами, ведь по параметрам можно вычислить это распределение, и в случае, если оно содержит недопустимые значения, сделать выводы о несуществовании кода. В ближайшее время, используя рассматриваемые результаты, планируется создать таблицу параметров полностью регулярных кодов для малых длин. Отметим, что исследование полностью регулярных кодов важно как с точки зрения теории кодирования, поскольку этот класс включает в себя важные подклассы оптимальных кодов, так и с точки зрения алгебраической комбинаторики, поскольку эти объекты в определенном смысле являются делителями графа гиперкуба.
[1] А. Ю. Васильева Сильная дистанционная инвариантность совершенных двоичных кодов. Дискретн. анализ и исслед. опер., сер. 1, 9:4 (2002), 33-40. http://mi.mathnet.ru/da183
[2] А. Ю. Васильева Локальные и межвесовые спектры вполне регулярных кодов и совершенных раскрасок. Пробл. передачи информ., 45:2 (2009), 84-90. http://dx.doi.org/10.1134/S0032946009020069
[3] D. S. Krotov “On Calculation of the Interweight Distribution of an Equitable Partition”, Journal of Algebraic Combinatorics, 40:2 (2014), 373-386. http://dx.doi.org/10.1007/s10801-013-0492-3
30. Получена точная верхняя оценка числа бент-функций, находящихся на минимальном расстоянии от произвольной бент-функции.
Бент-функции – булевы функции от чётного числа переменных, обладающие максимальной нелинейностью (под нелинейностью подразумевается расстояние Хэмминга от функции до множества всех аффинных функций). Максимальная нелинейность - одно из важнейших криптографических свойств булевых функций. Бент-функции тесно связаны и с многими дискретными объектами, такими как матрицы Адамара, разностные множества, сильно регулярные графы.
В работе рассматриваются метрические свойства класса бент-функций, важные для проблемы их классификации. Исследуется расположение двух бент-функций на минимально возможном расстоянии d друг от друга. Получена верхняя оценка числа бент-функций, находящихся на расстоянии d от произвольной бент-функции. Доказано, что оценка является точной и достигается только на квадратичных бент-функциях. Таким образом, в классе всех бент-функций данное метрическое свойство является характеристическим для множества квадратичных бент-функций.
1. Н. А. Коломеец Перечисление бент-функций на минимальном расстоянии от квадратичной бент-функции
// Дискретн. анализ и исслед. опер., 2012, T. 19, № 1, 41–58.
2. Н. А. Коломеец Пороговое свойство квадратичных булевых функций // Дискретн. анализ и исслед. опер., 21:2 (2014), 52–58.
3. Н. А. Коломеец Верхняя оценка числа бент-функций на расстоянии 2^k от произвольной бент-функции от 2k переменных // Прикл. дискрет. матем., 2014, № 3, 28–39.
31. Построены спектры распадов X(3872) с хорошими аналитическими и унитарными свойствами, которые позволяют определить относительную интенсивность распада
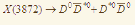 , изучая дополнительно только ещё один распад. Определена область значений для константы связи X(3872)-резонанса с тяжёлыми кваркониями , изучая дополнительно только ещё один распад. Определена область значений для константы связи X(3872)-резонанса с тяжёлыми кваркониями
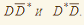 Показано, что построенные спектры позволяют эффективно оценивать различные теоретические сценарии для структуры X(3872)-мезона. Показано, что построенные спектры позволяют эффективно оценивать различные теоретические сценарии для структуры X(3872)-мезона.
Что можно узнать из интенсивности распада экзотической резонансной структуры X(3872) на тяжёлые кварконии
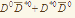 ? ?
Загадочное дитя спектроскопии чармония - резонанс X(3872), открытый десять лет назад, породил поток интерпретаций и положил начало экзотической XYZ-спектроскопии тяжёлых кваркониев, в которой мезоны являются четырёхкварковыми, по крайней мере. Между тем многие (если не все) характеристики резонанса X(3872) не ясны. В работе построены спектры распадов X(3872) с хорошими аналитическими и унитарными свойствами, которые позволяют определить относительную интенсивность распада 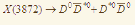 , изучая дополнительно только ещё один распад, например, , изучая дополнительно только ещё один распад, например,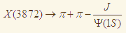 . Определена область значений для константы связи X(3872)-резонанса с тяжёлыми кваркониями . Определена область значений для константы связи X(3872)-резонанса с тяжёлыми кваркониями
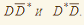 Показано, что построенные спектры позволяют эффективно оценивать различные теоретические сценарии для структуры X(3872)-мезона. Показано, что построенные спектры позволяют эффективно оценивать различные теоретические сценарии для структуры X(3872)-мезона.
N. N. Achasov, E. V. Rogozina How learn the branching ratio
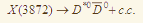 Письма в ЖЭТФ, 2014, том 100, выпуск 4, стр. 252-255 Письма в ЖЭТФ, 2014, том 100, выпуск 4, стр. 252-255
|









