Важнейшие научные результаты Института математики за 2013 год

1. Классифицированы центральные простые конечномерные некоммутативные йордановы супералгебры характеристики 0.

Классическим результатом теории йордановых алгебр является координатизационная теорема Джекобсона, сводящая изучение йордановых алгебр с набором из N>2 определенным образом связанных идемпотентов к изучению эрмитовых матриц над альтернативными алгебрами. Обобщение этой теоремы на класс некоммутативных йордановых алгебр было получено Маккримоном. В нашей работе доказана координатизационная теорема для некоммутативных йордановых супералгебр степени N>2, описывающая такие алгебры. Доказано, что симметризованная йорданова супералгебра для простой конечномерной некоммутативной йордановой супералгебры характеристики 0 и степени N>1 является простой. Классифицированы центральные простые конечномерные некоммутативные йордановы супералгебры характеристики 0.
Как следствие, описаны скобки Пуассона на простых конечномерных йордановых супералгебрах характеристики 0.

Пожидаев А. П., Шестаков И. П. Простые конечномерные некоммутативные йордановы супералгебры характеристики 0 // Сиб. мат. журн. – 2013. – Т. 54. – № 2. – С. 389-406.
Пожидаев А. П., Шестаков И. П. Некоммутативные йордановы супералгебры степени n≥2 // ДАН 431. – 2010. – № 2. – С. 165-169.
Пожидаев А. П., Шестаков И. П. Некоммутативные йордановы супералгебры степени n>2 // Алгебра и Логика. – 2010. –
Т. 49. – № 1. – С. 26-59.

2. Доказано, что существует лишь конечное число логик над известной модальной логикой S4, обладающих ограниченным интерполяционным свойством или проективным свойством Бета. Отсюда следует разрешимость над S4 всех основных вариантов интерполяционного свойства и свойства Бета.

Установлено, что все основные варианты интерполяционного свойства и свойства Бета разрешимы над модальнрй логикой S4.
Имеются 4 основных варианта интерполяционного свойства и 4 варианта свойства определимости по Бету. Исследование было начато в 1979 году, когда было доказано, что имеется лишь конечное число расширений широко известной модальной логики S4, обладающих интерполяционным свойством Крейга, и это свойство разрешимо над логикой S4. На последнем этапе построена эффективная классификация расширений логики S4. Доказано, что существует лишь конечное число логик над S4, обладающих ограниченным интерполяционным свойством IPR или проективным свойством Бета PBP, найдена верхняя оценка количества таких логик. Все эти логики финитно аппроксимируемы, разрешимы и узнаваемы над S4, откуда следует разрешимость ограниченной интерполяции и проективного свойства Бета над S4.

Максимова Л. Л. Ограниченная интерполяция над модальной логикой S4 // Алгебра и логика. – 2013. – Т. 52. – № 4. –
С. 461-501.

3. Доказано, что автоморфизм дистрибутивной решетки определяется неподвижными элементами тогда и только тогда, когда он является инволюцией. Получено полное описание подалгебр булевых алгебр, которые являются неподвижными подалгебрами автоморфизмов, определяемых неподвижными элементами.

Исследуются обогащенные булевы алгебры. Решён вопрос, поставленный С.С.Гончаровым: когда по подалгебре булевой алгебры однозначно восстанавливается автоморфизм, для которого данная подалгебра является подалгеброй неподвижных элементов. Получено полное описание подалгебр булевых алгебр, которые являются неподвижными подалгебрами автоморфизмов, определяемых неподвижными элементами; показано, что класс таких булевых алгебр с выделенной подалгеброй является конечно аксиоматизируемым.
Исследованы подалгебры неподвижных элементов автоморфизмов атомных и суператомных булевых алгебр; показано, что подалгебра неподвижных элементов автоморфизма атомной булевой алгебры определяет его тогда и только тогда, когда она имеет ширину 2. Получен критерий элементарной эквивалентности таких булевых алгебр с выделенной подалгеброй.
Доказано, что автоморфизм дистрибутивной решетки определяется неподвижными элементами тогда и только тогда, когда он является инволюцией; показано что даже для конечных модулярных решёток это не верно.

Пальчунов Д. Е., Трофимов А. В. Локальные и неисчезающие суператомные булевы алгебры с выделенной плотной подалгеброй // Алгебра и логика. – 2011. – Т. 50. – № 6. – С. 822-847.
Пальчунов Д. Е., Трофимов А. В. Автоморфизмы булевых алгебр, определяемые неподвижными элементами // ДАН. – 2012. – Т. 443. – № 1. – С. 14-15.
Пальчунов Д. Е., Трофимов А. В. Автоморфизмы булевых алгебр, определяемые неподвижными элементами // Алгебра и логика. – 2012. – Т. 51. – № 5. – С. 623-637.

4. Описаны условия сильной конструктивизируемости булевых алгебр в терминах вычислимости последовательности канонических предикатов Ершова-Тарского на булевых алгебрах.

Решена известная задача о связи сильной конструктивизируемости булевых алгебр фиксированной элементарной теории и вычислимости некоторых наборов канонических предикатов на них, куда входят идеалы из последовательности Ершова-Тарского, а также множества, соответствующие множествам атомов, идеалам безатомных, идеалам атомных элементов фактор-алгебр по идеалам последовательности Ершова-Тарского. Задача решена для булевых алгебр всех элементарных характеристик, для булевых алгебр элементарной характеристики (infinity, 0, 0) дополнительно налагается условие равномерной вычислимости рассматриваемой последовательности предикатов.

Леонтьева М. Н. Существование сильно вычислимых представлений в классе булевых алгебр // Доклады АН. – 2012. – Т. 445. – № 2. – С.132-134.
Леонтьева М. Н. Минимальность некоторых условий разрешимости для булевых алгебр // Сиб. мат. журн. – 2012. – Т. 53. – № 1. – С. 132-147.
Леонтьева М. Н. Достаточные условия разрешимости для булевых алгебр // Вестн. НГУ. Серия: Математика, механика, информатика. – 2011. – Т.11. – № 4. – С. 63-68.
Леонтьева М. Н. Булевы алгебры характеристики (1,0,1) с вычислимыми множеством атомов и идеалом Ершова-Тарского // Алгебра и логика. – 2011. – Т. 50. – № 2. – С. 133-151.
Леонтьева М. Н. Булевы алгебры характеристики (1,0,1) с вычислимыми множеством атомов и идеалом атомных элементов // Вестник НГУ. Серия: математика, механика, информатика. – 2010. – Т. 10. – № 1. – С. 65-69.
Леонтьева М. Н. Сильная конструктивизируемость булевых алгебр // Диссертация на соискание ученой степени кандидата физико-математических наук, 2013, Институт математики СО РАН, 67 с.

5. Описаны абелевы группы, теории которых являются P-стабильными для основных типов подгрупп P.

Понятие P-стабильности является обобщением классического понятия стабильности, фундаментального понятия современной теории моделей. Заметим, что из элиминации кванторов, доказанной В. Шмелев, вытекает классическая стабильность теории любой абелевой группы. Что касается P-стабильности абелевых групп, то отметим здесь результаты Т. А. Нурмагамбетова и М. А. Русалеева. Первый показал [1], что при обобщенной континуум-гипотезе теория любой абелевой группы будет P-стабильной, если P определяет элементарную подсистему. М. А. Русалеев доказал [2], что теория любой абелевой группы без кручения будет P-стабильной, если P определяет алгебраически замкнутую подгруппу. Сформулируем более подробно утверждения из обсуждаемого результата. Четыре типа P-стабильности из формулировки результата будем называть соответственно (P,s)-стабильностью, (P,e)-стабильностью, (P,p)-стабильностью и (P,a)-стабильностью. Доказано, что теория любой абелевой группы является (P,e)-стабильной, и (P,p)-стабильной. Теория абелевой группы A является (P,s)-стабильной тогда и только тогда, когда она представляет собой конечную прямую сумму элементарных абелевых групп и конечной группы. Теория абелевой группы A является (P,a)-стабильной тогда и только тогда, когда она удовлетворяет следующим двум условиям: (1) для любого простого числа p подгруппа (pA)[p] группы A конечна, (2) для любого простого числа p либо подгруппа A[p] группы A конечна, либо ее шмелевский инвариант гамма(p) конечен. Ясно, что из этих утверждений вытекают результаты Нурмагамбетова и Русалеева.
Список литературы:
[1] Т. А. Нурмагамбетов P-стабильность полных теорий абелевых групп, XI Межреспубл. конф. по мат. логике. Тез. сообщений, Казань, изд-во КГУ, 1992, с. 106.
[2] М. А. Русалеев Обобщенная стабильность абелевых групп без кручения, Алгебра и логика, т. 50, № 2 (2011), c. 231-245.

Палютин Е. А. P-суперстабильные абелевы группы // Вестник Карагандинского государственного университета. Серия математика. – 2013. – № 1(69). – С. 74-81.
Палютин Е. А. Число P-обогащений абелевых групп // Алгебра и логика. – 2013. – Т. 52. – № 2. – С. 255-258.
Палютин Е. А. P-обогащения абелевых групп // Труды Международной научно-практической конференции Современная математика: проблемы и приложения, посвященная научно-педагогической деятельности академика А. Д. Тайманова,
г. Кзылорда (Казахстан). – 2013. – С. 21-31.
Палютин Е. А. P-стабильные абелевы группы // Алгебра и логика. – 2013. – Т. 52. – № 5. – С. 606-631.

6. Изучены свойства и представления подгрупп конечного индекса групп Баумслага-Солитера

Группы Баумслага-Солитера задаются порождающими и соотношениями
        BS(p,q)=<a,t|t^-1a^pt=a^q>, p,q - целые параметры.
При различных простых параметрах, не равных единице, в терминах графов групп описаны все подгруппы групп BS(p,q). При взаимно простых целых параметрах, не равных нулю, описаны подгруппы конечного индекса групп BS(p,q) (найдены их копредставления, решена проблема изоморфизма) и найдены все их неприводимые представления над C. При взаимно простых целых параметрах, не равных 0,1,-1, описана структура абстрактного соизмерителя групп BS(p,q).

Дудкин Ф. А. Подгруппы конечного индекса в группах Баумслага—Солитера // Алгебра и логика. – 2010. – Т. 49. – № 3. – С. 331—345.
Дудкин Ф. А. Об абстрактном соизмерителе групп Баумслага—Солитера // Алгебра и логика. – 2013. – Т. 52. – № 1. – С. 64—83.
Дудкин Ф. А. Подгруппы групп Баумслага—Солитера // Алгебра и логика. – 2009. – Т. 48. – № 1. – С. 3-30.
Дудкин Ф. А. Неприводимые представления подгрупп конечного индекса групп Баумслага—Солитера // Сибирский математический журнал. – 2013. – Т. 54. – № 6. – С. 1273-1279.

7. Решена проблема распознаваемости знакопеременных групп по спектру.

Спектром группы называется множество порядков ее элементов. Будем говорить, что конечная группа G распознаваема по спектру, кратко, распознаваема, если для любой конечной группы H из равенства спектров групп G и H следует их изоморфизм. В 1983 г. Ши показал, что знакопеременная группа степени 5 распознаваема. В следующие 30 лет частичные результаты о распознаваемости знакопеременных групп были получены в работах ряда авторов, среди которых выделим Брандла, Прегер, Мазурова, Кондратьева, Заварницина и Вакулу. Совокупность этих результатов можно резюмировать следующим образом: для каждого простого числа p>5 группы A_{p}, A_{p+1}, A_{p+2} распознаваемы, так же как и группы A_n при 5\leq n\leq25 и n\neq 6, 10, а группы A_2, A_3, A_4, A_6 и A_{10} нераспознаваемы. В нашей работе доказывается, что все знакопеременные группы степени, большей 25, распознаваемы по спектру. Таким образом, получен полный ответ на вопрос о распознаваемости знакопеременных групп. Кроме того, с учетом имеющихся результатов, из этого утверждения следует, что любая конечная группа со спектром как у неабелевой простой группы имеет не более одного неабелева композиционного фактора.

Горшков И. Б. // Алгебра и логика. – 2013. – Т. 52. – № 1. – С. 57-63.

8. Доказана локальная конечность групп периода 12, не содержащих элементов порядка 12.

Группа G называется группой периода n, если порядок любого элемента группы G делит n. Вопрос о том, будет ли конечной группа периода n, порожденная конечным числом элементов, восходит к У. Бернсайду. Известно, что проблема Бернсайда имеет отрицательное решение для больших n, а для малых n вопрос до конца не исследован. Получены условия, обеспечивающие локальную конечность групп периода 12. В частности, доказано, что группы периода 12 без элементов порядка 12 локально конечны.

Лыткина Д. В., Мазуров В. Д., Мамонтов А. С. Локальная конечность некоторых групп периода 12 // Сиб. матем. журн.
– 2012. – Т. 53. – № 6. – С. 1373-1378
Мазуров В. Д., Мамонтов А. С. Инволюции в группах периода 12 // Алгебра и логика. – 2013. – Т. 52. – № 1. – С. 92-98
Мамонтов А. С. Группы периода 12 без элементов порядка 12 // Сиб. матем. журн. – 2013. – Т. 54. – № 1. – С. 150-156

9. Доказано, что позитивная логика и логика Иоганссона разрешимы по допустимости и обладают унификацией конечного типа.

Данная работа начинает изучение допустимых правил вывода и унификации в логиках со слабым (паранепротиворечивым) отрицанием, или вообще без него. Доказано, что множество правил вывода с параметрами допустимых в позитивной интуиционистской логике является разрешимым. С помощью данного результата доказывается, что позитивная интуиционистская логика обладает унификацией конечного типа, т.е. по любой формуле рапознается, унифицируема она или нет в данной логике, а в случае позитивного ответа эффективно строится конечное множество ее наиболее общих унификаторов. Аналогичные результаты получены для минимальной логики Иоганссона. Сложность доказательства обусловлена невозможностью использовать трансляцию Геделя-Тарского, в тоже время, предложенная конструкция может служить основой для исследования допустимости и унификации в широком классе логик имеющих тот же позитивный фрагмент, что и интуиционистская логика.

Odintsov S. P., Rybakov V. V. Unification and admissible rules for paraconsistent minimal Johannson's logic J and positive intuitionistic logic IPC⁺ // Ann. Pure

10. Доказана формула коплощади для гладких контактных отображений пространств Карно-Каратеодори.

Для отображений, определенных на многообразиях Карно и принимающих значения на пространствах Карно-Каратеодори, доказана формула коплощади. В частности, исследовано поведение римановой и субримановой мер на множествах уровня. Впервые рассмотрены отображения, образ которых имеет неголономную структуру. Следовательно, результат является новым и для модельного случая отображений из группы Карно в группу Карно.

Karmanova M., Vodopyanov S. Acta Applicanda Mathematicae. – 2013. – V. 128. – P. 67-111. DOI: 10.1007/
s10440-013-9822-7

11. Построен алгоритм вычисления топологических характеристик трехмерных тел, основанный на дискретизации теории Морса. Построенный алгоритм применен для оценки топологических характеристик случайных полей, возникающих при численном моделировании нефтегазовых коллекторов.

В различных прикладных областях современной науки возникает задача вычисления топологических характеристик геометрических объектов сложной формы. Это привело к появлению вычислительной топологии, которая бурно развивается в последнее время. Как правило, задача вычислительной топологии сводится к эффективному вычислению чисел Бетти, т.е. рангов групп гомологий. В работе [1] предлагается метод вычисления чисел Бетти трехмерных тел, основанный на дискретизации теории Морса. При этом тела задаются посредством объединения единичных кубиков с целочисленными координатами вершин в трехмерном евклидовом пространстве. Главной особенностью предложенного подхода является использование дискретных аналогов гладких функций, которые кроме стандартных невырожденных (морсовских) критических точек имеют также простейшие вырожденные критические точки – точки типа “обезьянего седла”. В [2] разработанный алгоритм применяется для вычисления топологических характеристик реализаций случайных полей, применяемых при численном моделировании коллекторов.

[1] Базайкин Я. В., Тайманов И. А. Об одном численном алгоритме вычисления топологических характеристик трехмерных тел // Ж. вычисл. матем. и матем. физ. – 2013. – Т. 53. – № 4. – С. – 523-530.
[2] Базайкин Я. В., Байков В. А., Тайманов И. А., Яковлев А. А. Численный анализ топологических характеристик трехмерных геологических моделей нефтегазовых месторождений // Матем. Моделирование. – 2013. – Т. 25. – № 10.
– С. 19-31.

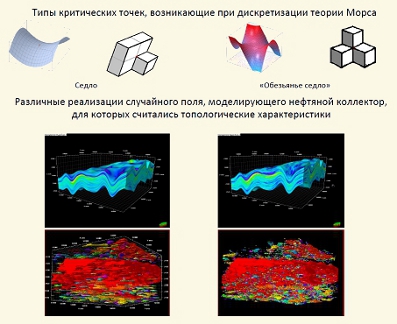
12. Доказано утверждение теоремы Морса-Сарда для соболевских классов.

Доказано утверждение теоремы Морса-Сарда для функций соболевского класса W^n_1(R^n). Кроме того, для этих функций установлено N-свойство Лузина относительно 1-меры Хаусдорфа. Использованием этих результатов показано, что почти все множества уровня таких функций суть C^1-гладкие компактные многообразия размерности n-1. Перечисленные результаты верны также для более широкого класса функций BV_n(R^n) (у которых производные порядка n являются мерами Радона). В ходе исследований установлены теоремы об аппроксимации соболевских функций гладкими с исключительным множеством малой хаусдорфовой вместимости.

Bourgain J., Korobkov M. V. and Kristensen J. On the Morse-Sard property and level sets of W^{n,1} Sobolev functions on R^n // Journal fur die reine und angewandte Mathematik (Crelles Journal)} (Online first), http://dx.doi.org/10.1515/crelle-2013-0002, March 2013.
Bourgain J., Korobkov M. V. and Kristensen J. On the Morse – Sard property and level sets of Sobolev and BV functions // Rev. Mat. Iberoam. – 2013. – V. 29. – № 1. – P. 1-23.

13. Найден симметрический вид уравнений релятивистской магнитной гидродинамики в терминах физических переменных, который затем использован для нахождения условий корректности задачи с релятивистской свободной границей "плазма-вакуум" и задачи для релятивистского тангенциального разрыва.

Отталкиваясь от вычислений в системе покоя жидкости и применяя преобразование Лоренца, найден симметрический вид уравнений релятивистской магнитной гидродинамики (РМГД) в терминах "примитивных" (физических) неизвестных. Построено также семейство так называемых вторичных симметризаций системы РМГД. Найденный конкретный вид симметрических матриц важен для исследования начально-краевых задач для системы РМГД. С помощью полученных симметризаций найдены достаточные условия корректности в пространствах Соболева задачи с релятивистской свободной границей "плазма-вакуум" и задачи для релятивистского тангенциального МГД разрыва. Для первой из названных задач важным моментом явилось также использование вторичной симметризации уравнений Максвелла в вакууме.

Trakhinin Y. Stability of relativistic plasma-vacuum interfaces // Journal of Hyperbolic Differential Equations. – 2012.
– V. 9. – P. 469-509.
Freistühler H., Trakhinin Y. Symmetrizations of RMHD equations and stability of relativistic current-vortex sheets // Classical and Quantum Gravity. – 2013. – V. 30. – P. 17. 085012.

14. Предложена модернизация уравнения состояния в среде с токами для классических уравнений Максвелла.

Годунов С. К. // ЖВМиМФ. – 2012. – Т. 52. – № 5. – С. 916-929
Годунов С. К. // ЖВМиМФ. – 2013. – Т. 53. – № 8. – С. 130-133

15. Предложен подход, позволяющий исследовать асимптотическое поведение распределений двухшаговых статистических оценок при близких к минимальным ограничениях как на точность оценки первого шага, так и на гладкость функций, определяющих оценки второго шага.

Двухшаговые статистические оценки широко применяются в прикладных статистических исследованиях при оценивании неизвестного параметра. Однако зачастую они используются без соответствующего теоретического обоснования, поскольку принято считать, что они дают достаточно точные приближения для оптимальных в некотором смысле оценок. Последнее действительно имеет место в целом ряде частных случаев благодаря соображениям, изложенным в основополагающей работе Р. А. Фишера (1925). Причем во всех известных авторам доказательствах асимптотической нормальности таких оценок предполагается существование достаточно гладких производных у основных функций, которые определяют оценки второго шага, и накладываются серьезные ограничения на точность оценки первого шага.
В 2000 – 2012 годах авторы опубликовали цикл работ, в которых построили асимптотически нормальные двухшаговые статистические оценки в ряде задач регрессии при более слабых ограничениях, когда не нужно существования производных у основных функций, а от оценок первого шага часто требуется лишь обычная состоятельность. Идеи доказательств результатов цикла удалось в работе [1] представить в виде общего подхода к изучению асимптотического поведения двухшаговых статистических оценок.
Наиболее ограничительное условие в [1] – это предположение о том, что оценка первого шага является дробно-линейной функцией от наблюдений. В [2] в случае одномерного неизвестного параметра это требование ослаблено.
В результате, метод работы [1] удалось распространить на более широкие классы оценок первого и второго шага, которые содержат знаменитые М-оценки, в том числе построенные по разнораспределенным наблюдениям в схеме серий. В итоге, при ограничениях, близких к минимальным, метод позволяет находить необходимые и достаточные условия слабой сходимости нормированной разности двухшаговой оценки и параметра к произвольному распределению.

[1] Линке Ю. Ю., Саханенко А. И. Об асимптотике распределения одного класса двухшаговых статистических оценок многомерного параметра // Математические труды. – 2013. – Т.16. – №1. – С. 89-120.
[2] Линке Ю. Ю., Саханенко А. И. Об асимптотике распределения двухшаговых статистических оценок одномерного параметра // Сибирские электронные математические известия. – 2013. – Т. 10. – С. 627-640.

16. Завершен цикл работ, связанных с исследованием распределения времени пребывания случайного блуждания в отрезке и на полуоси. Получены полные асимптотические разложения в локальной предельной теореме о времени пребывания случайного блуждания на полуоси с удаляющейся границей.

Изучение распределения времени пребывания случайного блуждания на отрезке или на полуоси является интересной, но в то же время весьма трудной задачей, и ей посвящено значительное число работ. Хорошо известен классический закон арксинуса, характеризующий предельное поведение распределения времени пребывания на положительной полуоси. В монографиях А. В. Скорохода и Н. П. Слободенюка (1970), А. Н. Бородина и И. А. Ибрагимова (1994) получены предельные теоремы о времени пребывания, основанные на использовании сходимости распределений весьма сложных функционалов от траекторий случайного блуждания к распределению соответствующих функционалов от предельных процессов.
Как правило, одним из следующих шагов после получения предельных теорем является нахождение асимптотических разложений. Это и явилось основной целью представленного цикла работ. Исследование проводилось с помощью факторизационного метода, который был разработан в Новосибирске и успешно применялся для решения ряда граничных задач для случайных блужданий и процессов. На первом этапе удалось найти факторизационные представления для интегральных преобразований над искомыми распределениями (2010), затем был выполнен асимптотический анализ этих представлений при выполнении условия Крамера на распределение скачков блуждания (2010, 2012), что позволило затем на третьем этапе (2013) получить полные асимптотические разложения для распределения времени пребывания случайного блуждания на полуоси с удаляющейся границей.

Лотов В. И. Факторизационные тождества для времени пребывания случайного блуждания в полосе // Сибирский математический журнал. – 2010. – Т. 51. – №1. – С. 146-155.
Лотов В. И. О времени пребывания случайного блуждания в полосе // Сибирский математический журнал. – 2010.
– Т. 51. – № 4. – С. 785-804.
Лотов В. И. О сходимости распределения времени пребывания случайного блуждания на полуоси // Вестник НГУ. Серия: Математика, механика, информатика. – 2012. – Т. 12. – № 2. – С. 56-60.
Лотов В. И. Асимптотические разложения распределения времени пребывания случайного блуждания на полуоси
// Труды МИ АН. – 2013. – Т. 282. – № 3. – С. 154-164.

17. Доказана локальная теорема восстановления в случае, когда распределение шага в случайном блуждании сосредоточено на целочисленной решетке и имеет бесконечное математическое ожидание.

Исследуется асимптотика локальной вероятности восстановления при условии, что плотность распределение шага в случайном блуждании относительно считающей меры правильно меняется на бесконечности. В свое время Гарсия и Ламперти (1963) получили асимптотическое представление для локальной вероятности восстановления в случае, когда распределение шага притягивается к устойчивому закону с показателем, не превосходящим 1, но большим, чем 1/2. Позже Вильямсон (1968) показал, что в случае, когда показатель устойчивого закона, к которому притягивается распределение шага, меньше или равен 1/2, для правильного поведения локальной вероятности восстановления нужны дополнительные условия. Разумеется, используемое нами условие является более сильным, нежели притяжение к устойчивому закону.

Nagaev S. V. Renewal theorems in the case of attraction to the stable law with characteristic exponent smaller than unity
// Annales Mathematicae et Informaticae. – 2012. – V. 39. – P. 173-191.

18. Разработан сплайновый метод определения скоростных характеристик среды вблизи скважины по данным вертикального сейсмического профилирования.

В процессе вертикального сейсмического профилирования регистрируются времена первого вступления продольных сейсмических волн от пунктов взрыва до приемников, расположенных в вертикальной скважине. Предложенный метод решения обратной кинематической задачи об определении скоростной характеристики среды по данным вертикального сейсмического профилирования основан на комбинированном использовании уравнения эйконала и сплайновых методов аппроксимации функций многих переменных. Задача решается в предположении горизонтально-слоистого строения среды; однако никаких предположений о количестве слоев и их толщине не делается. Вначале по данным о временах первого вступления сейсмического сигнала строится сплайн, аппроксимирующий время прихода сигнала из источников возбуждения в любую точку пространства. Затем с помощью уравнения эйконала определяется скорость распространения сигнала в среде. Результаты численных экспериментов с модельными и реальными данными убедительно демонстрируют перспективность предложенных сплайновых алгоритмов определения скоростной характеристики среды в окрестности скважины.

Богданов В. В., Волков Ю. С., Карстен В. В., Мирошниченко В. Л. Сплайновая модель скоростной характеристики среды по данным вертикального сейсмического профилирования // Интеллектуализация обработки информации: 9-я международная конференция. Черногория, г. Будва, 2012 / Сборник докладов. – М.: Торус Пресс, 2012. – С. 514-517.
Bogdanov V. V., Karsten W. V., Miroshnichenko V. L., Volkov Yu. S. Application of splines for determining the velocity characteristic of a medium from a vertical seismic survey // Central European Journal of Mathematics. – 2013. – Vol. 11, n. 4. – P. 779-786.

19. Разработаны аналоги формул Ньютона-Котеса для интегрирования функций одной и двух переменных с быстро растущими погранслойными составляющими.

Предложен способ построения квадратурных формул для функций с большими градиентами. Способ основан на аддитивном выделении с точностью до множителя составляющей, задающей погранслойный рост интегрируемой функции и построении квадратурной формулы, точной на выделенной погранслойной составляющей. Интегрируемая функция представима в виде суммы регулярной составляющей с ограниченными производными до некоторого порядка и известной с точностью до множителя погранслойной составляющей, рассматриваемой как функция общего вида. Такое представление справедливо для решения сингулярно возмущенной краевой задачи. Для построения квадратурных формул используется разработанная авторами формула интерполяции, точная на заданной погранслойной составляющей, с произвольным числом узлов интерполяции. Построены и обоснованы квадратурные формулы с 2-5 узлами. Доказано, что построенные формулы имеют погрешность порядка O(h^n-1) , равномерно по погранслойной составляющей и ее производным, где n – число узлов формулы. Формулы Ньютона-Котеса для таких функций обладают только первым порядком точности. Предложенный подход применен к построению аналога кубатурной формулы Симпсона для функции двух переменных с погранслойными составляющими по каждой переменной.

Задорин А. И., Задорин Н. А. Квадратурные формулы для функций с погранслойной составляющей // Журнал вычислительной математики и математической физики. – 2011. – Т. 51. – № 11. – С. 1952-1962.
Zadorin A. I., Zadorin N. A. Interpolation formula for functions with a boundary layer component and its application to derivatives calculation // Сибирские электронные математические известия. – 2012. – Т. 9. – С. 445-455.
Задорин А. И., Задорин Н. А. Аналог формулы Ньютона-Котеса с четырьмя узлами для функции с погранслойной составляющей // Сибирский журнал вычислительной математики. – 2013. – Т. 16. – № 4. – С. 313-323.
Zadorin A., Zadorin N. Quadrature Formula with Five Nodes for Functions with a Boundary Layer Component // Lecture Notes in Computer Science. – 2013. – V. 8236. – P. 540-546. Springer, Heidelberg.
Задорин А. И. Кубатурные формулы для функции двух переменных с погранслойными составляющими // Журнал вычислительной математики и математической физики. – 2013. – Т. 53. – № 12. – С. 51-61.

20. Получена количественная и качественная (по устойчивости) классификация равновесий в модели международной торговли Диксита-Стиглица-Кругмана с асимметричным распределением иммобильного труда.

Традиционная модель Диксита-Стиглица-Кругмана (ДСК) имеет ограничения, противоречащие экономической реальности: (1) предположение о полной идентичности торгующих стран, что приводит к выводам (например, о существовании точки бифуркации), которые не являются устойчивыми при малых колебаниях параметров; (2) ограничение анализа только двумя торгующими регионами. Представленные работы посвящены исследованию ДСК-модели в случае снятия этих ограничений. В статье «Agglomeration and Spreading in an Asymmetric World» изучается двухрегиональная ДСК-модель с асимметричными регионами. Получена исчерпывающая классификация типов динамических картин миграционных потоков, параметризованных по степени свободы торговли и степени асимметрии распределения иммобильного труда. Вторая работа, «Устойчивость равновесий полной агломерации…», посвящена частичному обобщению результатов предыдущей статьи для многорегионального аналога ДСК-модели. Получены необходимые и достаточные условия устойчивости равновесий полной агломерации.

Sidorov A. V., Zhelobodko E. Agglomeration and Spreading in an Asymmetric World // Review of Development Economics.
– 2013. – № 17(2). – P. 201-219.
Сидоров А. В. Устойчивость равновесий полной агломерации в многорегиональной модели “Ядро-Периферия”
// Журнал Новой Экономической Ассоциации. – 2013. – № 17(1). – С. 44-62.

21. В математических моделях микроэлектромеханических резонаторов разного типа исследованы свойства нелинейных колебаний и условия их существования.

В связи с математическим моделированием электромеханических резонаторов на основе МЕМС (микроэлектромеханические системы) проведено исследование ряда математических моделей, описывающих нелинейные колебания подвижного электрода (недеформируемая платформа на пружине, натянутая плёнка, упругая балка), возникающих при воздействии электростатического притяжения в узком зазоре между подвижным и неподвижным электродами. Найдены условия на параметры модели, при выполнении которых колебания не сопровождаются соударениями с поверхностью неподвижного электрода.

Косцов Э. Г., Фадеев С. И. Новые микроэлектромеханические резонаторы для гигагерцевых частот // Автометрия.
– 2013. – Т. 49. – № 2. – С. 115-122.
Фадеев C. И., Пиманов Д. О. Исследование периодических решений в математических моделях микромеханики при импульсном периодическом воздействии // Вестник Новосибирского государственного университета.
Серия: Математика, механика, информатика. – 2013. – Т.13. – № 3. – С. 122-140.
Фадеев C. И., Пиманов Д. О. Численное исследование математических моделей микромеханики при периодическом импульсном воздействии // Сибирский журнал индустриальной математики. – 2013. – Т.XVI. – №3(55). – С. 133-145.
Косцов Э. Г., Фадеев С. И. О функционировании СВЧ микромеханического резонатора // Сибирский журнал индустриальной математики. – 2013. – Т. XVI. – №4(56). – С. 75-86.

22. Получена полная характеризация циклов малой длины в Pancake графе.

Исследуется циклическая структура Pancake графа, являющегося графом Кэли на симметрической группе с порождающим множеством всех префикс-реверсалов.
Данный граф известен в связи с открытой Pancake problem, состоящей в определении его диаметра. Ранее было показано, что в данном графе содержатся все циклы длин от 6 до n! Однако, вопрос о характеризации циклов (их описание и число) оставался открытым. В настоящей работе разработан метод, основанный на иерархическом строении Pancake графа, позволяющий описывать и перечислять его циклы.
Получена полная характеризация циклов малой длины. Данный метод работает также на других графах Кэли, имеющих иерархическое строение, в частности, на Star графе.

Константинова Е. В., Медведев А. Н. Циклы длины семь в Pancake графе // Дискретный Анализ и Исследование Операций. – 2010. – Т. 17. – С. 46-55.
Константинова Е. В., Медведев А. Н. Циклы длины девять в Pancake графе // Дискретный Анализ и Исследование Операций. – 2011. – Т. 18. – С. 33-60.
Konstantinova E., Medvedev A. Small cycles in the Pancake graph // Ars Mathematica Contemporanea. – 2014. - № 7.
– P. 237-246. (published online 26 April 2013)
Konstantinova E. Some problems on Cayley graphs // Koper: University of Primorska Press. – 2013. – (Famnit lectures, ISSN 2335-3708; 1).
(http://www.hippocampus.si/ISBN/978-961-6832-51-9/index.html)

23. Доказано, что любой граф, не содержащий 3-циклов и 6-вершинных индуцированных подграфов, состоящих из двух цепей длины 2, является 4-раскрашиваемым.

Задачи о раскраске графов, не содержащих индуцированных подграфов из заданного класса C, представляют большой интерес (собственно, самая первая задача о раскраске – гипотеза о 4-х красках – относится как раз к такому типу задач). Этот интерес связан с тем, что любой наследственный класс графов можно задать множеством запрещенных подграфов. Особый интерес вызывает случай, когда это множество конечно и сравнительно невелико. Будет ли в этом случае хроматическое число таких графов ограничено, и если да, то чему может быть равно максимальное из них? Ясно, что для ограниченности хроматического числа один из подграфов должен быть полным.
Из теоремы Эрдеша вытекает, что еще один из подграфов должен быть лесом. Однако даже для графов с двумя запрещенными подграфами, один из которых является треугольником, а другой – лесом со сравнительно малым числом вершин, задача определения максимального хроматического числа остается довольно сложной и далекой от полного решения.
В настоящей работе показано, что любой граф, не содержащий треугольников и леса 2P_3, является 4-раскрашиваемым. Этот класс графов интересен тем, что с 2001 по 2010 он был единственным, для которого была неизвестна алгоритмическая сложность поиска хроматического числа, среди всех классов графов без треугольников и лесов с не более чем с 6 вершинами. Лишь в 2010 году Брусма, Головач, Лозин и Паулусма разработали весьма непростой алгоритм полиномиальной трудоемкости O(n^a) где a\ge15, определяющий хроматическое число графов без треугольников и 2P_3. При этом наиболее сложная и трудоемкая часть этого алгоритма состояла в различении графов с хроматическими числами 4 и 5. Из представляемого результата вытекает, что эта часть алгоритма совершенно не нужна, поскольку любой такой граф можно раскрасить в 4 цвета, причем такая раскраска строится за время O(n^3).

Pyatkin A. V. Triangle-free 2P3-free graphs are 4-colorable // Discrete Mathematics. – 2013. – V. 313. – P. 715–720.

24. Разработаны методы построения аддитивной комбинаторики на основе равномерно рекуррентных слов. В частности, показано, что свойство конечной суммируемости является регулярным относительно разбиения, а свойство бесконечной суммируемости – нет.

В серии работ совместно с Л. Замбони и М. Буччи проведено новое междисциплинарное исследование на стыке комбинаторики слов и аддитивной теории Рамсея. Подмножество натуральных чисел называется IP-множеством, если оно содержит все конечные суммы членов некоторой бесконечной последовательности натуральных чисел. Центральные множества являются особым классом IP-множеств, обладающим рядом дополнительных комбинаторных свойств. Введен новый метод построения IP-множеств и центральных множеств с помощью равномерно рекуррентных слов, в частности, слов Штурма и их обобщений, слова Туэ-Морса и других морфических слов. Упомянутые методы включают методы комбинаторики слов, топологических динамических систем, системы счисления, идемпотентные ультрафильтры и компактификацию Стоуна-Чеха. Для слова Туэ-Морса охарактеризованы аддитивные свойства множеств, задаваемых через вхождения факторов.
Наряду со свойством быть IP-множеством рассмотрены также два родственных аддитивных свойства, которые названы конечной и бесконечной суммируемостью. Подмножество A множества натуральных чисел назовем конечно (соотв., бесконечно) суммируемым если для каждого положительного натурального числа k множество A содержит конечные суммы с не более чем k слагаемыми из некоторой k-элементной (соотв., бесконечной) последовательности натуральных чисел.
Семейство S подмножеств натуральных чисел называется регулярным относительно разбиения, если всякое множество A из S обладает следующим свойством: для любого разбиения A на конечное число подмножеств хотя бы одно подмножество принадлежит S. Знаменитая теорема Хиндмана, 1974, говорит, что семейство IP-множеств является регулярным относительно разбиения. Показано, что свойство конечной суммируемости является регулярным относительно разбиения, а свойство бесконечной суммируемости – нет.

Bucci M., Hindman N., Puzynina S., Zamboni L. Q. Additive properties of sets defined by the Thue-Morse word // J. Comb. Theory (Series A). – 2013. – V. 120. – P. 1235-1245.
Bucci M., Puzynina S., Zamboni L. Q. Central sets generated by uniformly recurrent words // Ergodic Theory and Dynamical Systems. – 2013. – doi:10.1017/etds.2013.69.
Puzynina S., L. Q. Zamboni. Additive properties of sets and substitutive dynamics. A book chapter, to appear in a forthcoming book “Recent Mathematical Developments in Aperiodic Order” edited by J. Kellendonk, D. Lenz and J. Savinien.

25. Найден критерий вложимости собственной функции графа Джонсона с заданным собственным значением в некоторую собственную функцию графа Хэмминга с заданным собственным значением.

Собственной функцией графа называется собственный вектор матрицы смежности этого графа, соответствующий некоторому собственному значению, при этом собственная функция может быть тождественно нулевой. В силу того, что множество вершин графа Джонсона является подмножеством множества вершин графа Хэмминга, идея того, что собственные функции этих двух графов должны быть связаны, всегда казалась естественной. Впервые в явном виде получена такая связь в терминах вложимости: получен критерий вложимости собственной функции графа Джонсона с заданным собственным значением в некоторую собственную функцию графа Хэмминга с заданным собственным значением. Кроме того, получена явная формула, осуществляющая это вложение, и найден критерий его единственности.

Воробьев К. В. О вложении собственных функций графа Джонсона в собственные функции графа Хэмминга
// Дискретный анализ и исследование операций. – 2013. –Т. 20. – № 5. – С. 3–12.

26. Доказаны теоремы об “оптимальном” порядке переменных для одномерной задачи о рюкзаке в целочисленной и булевой постановках.

Выделен и исследован класс унимодулярных преобразований перестановочного типа, улучшающих структуру задачи о рюкзаке и некоторых ее обобщений, повышающих эффективность алгоритмов лексикографического перебора при их решении. Доказаны теоремы об “оптимальном” порядке переменных для одномерной задачи о рюкзаке в целочисленной и булевой постановках. Для алгоритма лексикографического перебора L классов и метода ветвей и границ построены и исследованы семейства задач целочисленного линейного программирования с L накрытиями экспоненциальной мощности, найдены унимодулярные преобразования, улучшающие их структуру. Выполнен анализ указанного лексикографического алгоритма для булевого варианта задачи о рюкзаке, получены новые оценки числа итераций, предложена и реализована его модификация с учетом специфики задачи, проведен вычислительный эксперимент.

Колоколов А. А., Орловская Т. Г., Рыбалка М. Ф. Исследование алгоритмов целочисленного программирования с использованием регулярных разбиений и унимодулярных преобразований // Автоматика и телемеханика. – 2012.
– № 2. С. 178-190.
Колоколов А. А., Орловская Т. Г. Исследование некоторых задач целочисленного программирования на основе унимодулярных преобразований и регулярных разбиений // Тр. Ин-та матем. и мех. УрО РАН. – 2013. – Т. 19. – № 2.
С. 193-202.
Колоколов А. А., Орловская Т. Г. Анализ алгоритмов решения некоторых задач о рюкзаке на основе L-разбиения // Алгебра и линейная оптимизация: тезисы междунар. конф., посвященной 100 летию С. Н. Черникова. Екатеринбург, 2012. С. 94 95.
Колоколов А. А., Орловская Т. Г. Исследование некоторых постановок задачи о рюкзаке и алгоритмов их решения с использованием унимодулярных преобразований и L-разбиения // Интеллектуализация обработки информации: 9-ая междунар. конф. Черногория, г. Будва, 2012 г.: Сборник докладов. М.: Торус Пресс, 2012. С. 286 289.
Орловская Т. Г. Улучшение структуры семейств задач о рюкзаке с использованием унимодулярных преобразований // Алгебра и линейная оптимизация: тезисы междунар. конф., посвященной 100 летию С. Н. Черникова. Екатеринбург, 2012. С. 122 124.

27. Доказано, что задача поиска в полном графе клики заданного размера с минимальной суммой весов входящих в неё вершин и ребер в общем случае не аппроксимируема. Для двух актуальных геометрических случаев задачи обоснованы алгоритмы квадратичной трудоемкости с гарантированными оценками точности, равными двум.

Рассмотрена задача поиска в полном неориентированном графе клики заданного размера с минимальной суммой весов входящих в нее вершин и ребер. Доказано, что в общем случае задача неаппроксимируема. Для двух специальных случаев задачи предложены приближенные полиномиальные алгоритмы квадратичной трудоемкости с оценками точности, равными двум. Установлено, что в случае метрического пространства гарантированная оценка точности алгоритма асимптотически достижима. Показано, что в случае, когда веса ребер равны квадратам попарных расстояний в некоторой системе точек многомерного евклидова пространства, полученная оценка точности алгоритма достижима.

Еремин И. И., Гимади Э. Х., Кельманов А. В., Пяткин А. В., Хачай М. Ю. 2-приближенный алгоритм поиска клики с минимальным весом вершин и рёбер // Труды Института механики и математики УрО РАНю – 2013. – Т. 19. – № 2.
– С. 134-143.
Доложено на конференциях:
Международная конференция «Дискретная оптимизация и исследование операций», DOOR-2013, Новосибирск, Академгородок, 24-28 июня 2013;
IV International Conference «Optimization and applications» (OPTIMA-2013), Petrovac, Montenegro, September 22 –28, 2013;
16-я Всероссийская конференция «Математические методы распознавания образов» (ММРО-16), г. Казань, 6 – 12 сентября 2013 г.

28. Для задачи поиска шара минимального радиуса, охватывающего фиксированное число точек из заданного конечного множества в евклидовом пространстве, доказано, что задача NP-трудна в сильном смысле, а также получена полиномиальная аппроксимационная схема, позволяющая решать задачу с произвольной относительной погрешностью.

Рассматривается задача поиска шара минимального радиуса, охватывающего не менее k точек из заданного конечного множества в евклидовом пространстве. В случае фиксированной размерности пространства задача полиномиально разрешима, но в общем случае сложностной статус задачи до настоящего времени не был установлен. Доказано, что задача NP-трудна в сильном смысле, а также получена полиномиальная аппроксимационная схема (PTAS), позволяющая решать задачу с произвольной относительной погрешностью ε за время O(dnα), где α =1+1/ε2,
d – размерность пространства, n – мощность исходного множества.

Шенмайер В. В. Задача о минимальном шаре, охватывающем k точек // Дискретный анализ и исслед. опер. – 2013.
– № 20:1. – С. 93-99.
Shenmaier V. V. Complexity and approximation in the smallest k-enclosing ball problem // Proceedings “The 7-h Conference on Combinatorics, Graph Theory and Applications (EuroComb 2013)”. Pisa, Italy, – P.583-588.

29. Предложен метод точного измерения масс и спинов частиц темной материи на линейных ускорителях. В основании метода лежит поиск сингулярностей в энергетическом спектре одиночного лептона.

Хиггсовский механизм и результаты LHC. Облако возможностей. В инертной дублетной модели (IDM) простейший вариант модели Хиггса дополнен набором D-частиц D, D^A, D⁺ , одна из которых (D) может оказаться частицей темной материи. Современные экспериментальные ограничения на массы новых частиц IDM получены из космологии (только для частиц темной материи) и из ускорительных данных. Обсуждается простой метод уточнения этих ограничений по данным коллайдера LEP и по будущим данным Международного линейного коллайдера (ILC). Для случая обнаружения этих частиц на ILC предложен метод определения масс этих частиц.
Модель допускает сильное взаимодействие D-частиц между собой при их слабом взаимодействии с наблюдаемыми ныне частицами.
Изучена эволюция параметров IDM с температурой в процессе охлаждения ранней Вселенной и построены возможные картины эволюции фазовых состояний Вселенной в процессе ее охлаждения с фазовыми переходами второго и первого рода. Одна из возможно возникающих фаз обладает неожиданными свойствами.

Ginzburg I. F. Measuring of mass and spin of dark matter particles at ILC // Phys. Part. Nucl. Lett. 9 (2012). – P. 678-685. Труды конференции.
Ginzburg I. F. Precise measuring mass and spin of Dark Matter particles at ILC via singularities in the single lepton energy spectrum. To be published in Proc. SPIN2012, JINR Physics of Particles and Nuclei. – 2014. – Vol. 45. – № 1. – P. 207-210. Труды конференции.