| |
Важнейшие научные результаты Института математики за 2009 год
1. Установлено, что экзистенционально замкнутые поля в классе счетных подполей классического кольца аделей являются так называемыми удивительными расширениями поля рациональных чисел.
Установлено, что экзистенционально замкнутые поля в классе счетных подполей классического кольца аделей являются так называемыми удивительными расширениями поля рациональных чисел.
Ю. Л. Ершов. О подполях кольца аделей // Алгебра и логика, 2009, 48, 6.
2. Для полурешеток степеней моделей по определимости с операцией скачка, согласованной с естественными вложениями полурешеток тьюринговых степеней и степеней перечислимости, доказана теорема об обращении скачка.
На основе введенного Ю. Л. Ершовым понятия системы, Σ-определимой (конструктивизируемой) в допустимом множестве, определяются отношения Σ-сводимости и Σ-эквивалентности на алгебраических системах. Полурешетки Σ-степеней позволяют получить оценку степени (относительной) конструктивной сложности для произвольной алгебраической системы, в том числе и несчетной, что невозможно в рамках классической теории конструктивных моделей.
Установлено существование естественных вложений полурешеток тьюринговых степеней и степеней перечислимости в полурешетки Σ-степеней, а также существование естественных гомоморфизмов полурешеток Σ-степеней в полурешетки степеней представимости. Показано, что полурешетки Σ-степеней с операцией скачка, согласованной с естественными вложениями полурешеток тьюринговых степеней и степеней перечислимости, обладают свойством обращения скачка. А именно, доказана
Теорема. Для любой системы
 с условием 0' ≤Σ с условием 0' ≤Σ
 , существует система , существует система
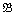 такая, что такая, что
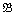 ' ≡Σ ' ≡Σ  .
Как следствие, установлено, что для полурешеток степеней представимости выполняется аналог теоремы об обращении скачка. Показано (совместно с О. В. Кудиновым), что образ операции скачка относительно естественного гомоморфизма полурешетки Σ-степеней в полурешетку степеней представимости по Мучнику имеет неподвижные точки. А именно, показано, что для системы .
Как следствие, установлено, что для полурешеток степеней представимости выполняется аналог теоремы об обращении скачка. Показано (совместно с О. В. Кудиновым), что образ операции скачка относительно естественного гомоморфизма полурешетки Σ-степеней в полурешетку степеней представимости по Мучнику имеет неподвижные точки. А именно, показано, что для системы  =(ω1CK,≤) выполнено =(ω1CK,≤) выполнено  ' ≡w ' ≡w  , где ≡w – эквивалентность по Мучнику , где ≡w – эквивалентность по Мучнику
Стукачев А. И., О степенях представимости моделей. I // Алгебра и логика, 2007, т. 46, стр. 763-788.
Стукачев А. И., О степенях представимости моделей. II // Алгебра и логика, 2008, т. 47, стр. 108-126.
Стукачев А. И., Теорема об обращении скачка для полурешеток Σ-степеней // Сибирские электронные математические известия, 2009, т. 6, стр. 182-190.
3. Завершена полная классификация суперинтуиционистских логик и расширений модальной логики Гжегорчика в соответствии с интерполяционными свойствами и свойствами неявной определимости.
Завершена полная классификация суперинтуиционистских логик и расширений модальной логики Гжегорчика Grz в соответствии с интерполяционными свойствами и свойствами неявной определимости. Доказано, что ограниченное интерполяционное свойство в указанных логиках равносильно проективному свойству Бета PB2. С учетом полученных ранее результатов, картина следующая. Из континуума суперинтуиционистских логик в точности 16 обладают ограниченным интерполяционным свойством и проективным свойством Бета, из них в точности 8 имеют интерполяционное свойство Крейга. Существуют в точности 13 расширений логики Гжегорчика с ограниченным интерполяционным свойством и проективным свойством Бета, среди них в точности 7 имеют интерполяционное свойство Крейга. Все эти логики полностью описаны. Все суперинтуиционистские логики и логики над Grz обладают слабым интерполяционным свойством и свойством Бета. Доказано, что все рассмотренные свойства разрешимы над Grz и над интуиционистской логикой.
Максимова Л. Л., Ограниченное интерполяционное свойство в суперинтуиционистских логиках // Алгебра и логика, 48, № 1 (2009), 54-89.
Maksimova L., Problem of restricted interpolation in superintuitionistic and some modal logics //Logic Journal of the IGPL, 2009; doi: 10.1093/jigpal/jzp040, 14 pp.
4. Доказана биинтерпретируемость с арифметикой ряда структур гомоморфно упорядоченных размеченных деревьев и лесов, возникших при изучении начальных сегментов полурешетки Вэджа (для случая k-разбиений).
Cтруктуры гомоморфно упорядоченных размеченных деревьев и лесов возникли при изучении начальных сегментов полурешетки Вэджа (для случая k-разбиений) в ряде работ P. Hertling и В. Л. Селиванова. Вопросы алебраического строения, разрешимости элементарной теории и группы автоморфизмов подобных структур, связанных с классическими сводимостями, всегда привлекали внимание специалистов. Также заметную роль при изучении других сводимостей (прежде всего Тьюринговой) играли различные гипотезы о биинтерпретируемости с арифметикой (2-го порядка для всей структуры степеней и 1-го порядка для локальной структуры), остающиеся по сей день нерешенными. Поскольку структуры k-размеченных лесов и деревьев не являются жесткими (их группы автоморфизмов при k>2 вычислены авторами и являются симметрическими Sk), естественно константно обогащать основной язык символами для одноэлементных деревьев, делая тем самым структуру жесткой. Установлено, что при таком обогащении при k>2 обе указанные структуры биинтерпретируемы с арифметикой. Для получения этого результата пришлось обобщать известную теорему Ганди, установив ее для широкого класса упорядоченных структур, без использования надстроечных допустимых множеств, а также устанавливать определимость операций скачка в данных структурах. Попутно, сходные результаты о биинтерпритируемости с арифметикой получены для классического порядка "быть подсловом" на словах конечного алфавита – при конечном константном обогащении языка символами для одно- и двухбуквенных слов. В частности, элементарная теория каждой из рассмотренных структур рекурсивно изоморфна теории арифметики.
Kudinov O. V., Selivanov V. L. Undecidability in the Homomorphic Quasiorder of Finite Labelled Forests // Journal of Logic and Computation, 17(6), 1135-1151 (2007)
Kudinov O. V., Selivanov V. L., Zhukov A. V. Definability in the h-quasiorder of labeled forests // Annals of Pure and Applied Logic, 2009, 159(3): 318-332.
Kudinov O. V., Selivanov V. L. Definability in the Infix Order on Words // Volker Diekert, Dirk Nowotka (Eds.): Proceedings of DLT 2009, Stuttgart, Germany, Lecture Notes in Computer Science, 2009, 5583, 454-465.
Kudinov O. V., Selivanov V. L. A Gandy Theorem for Abstract Structures and Applications to First-Order Definability // K. Ambos-Spies, B. Lowe, W. Merkle (Eds.): Proceedings of CiE 2009, Heidelberg, Germany, Lecture Notes in Computer Science, 2009, 5635,290-299.
5. Получены необходимые и достаточные условия существования структурной теории для Фреше-замкнутых классов.
А именно, доказана теорема о том, что если аксиоматизируемый класс алгебраических систем замкнут относительно приведенных степеней по фильтру Фреше и имеет стабильную некоммутативную теорию, то в этом классе можно проинтерпретировать класс всех графов. Из этого следует, что указанные выше классы не имеют какой-либо приемлемой структурной теории. С другой стороны, доказано, что коммутативные теории имеют достаточно богатую структурную теорию. Тем самым показано, что свойство коммутативности является необходимым и достаточным условием для указанных выше классов алгебраических систем иметь какую-либо нетривиальную структурную теорию.
Отметим полученные ранее результаты, относящиеся к этой теме. Построена богатая структурная теория классов колец над ассоциативными кольцами (Баур, Гараваглиа, Монк, Циглер, Прест). Доказана элиминация кванторов для коммутативных теорий над произвольным базисным множеством нормальных неприводимых формул, а также теорема об элиминации кванторов для слабо классифицируемых классов структур, замкнутых относительно приведенной степени по фильтру Фреше (Палютин). Это является обобщением теоремы Баура-Гараваглиа-Монка об аналогичной элиминации кванторов для класса всех модулей над ассоциативным кольцом. Из неструктурных результатов отметим результат об интерпретации класса всех графов в суперстабильных теориях со свойством DOP (Шелах). В конце 80-х годов было доказано, что что при условии суперстабильности условие коммутативности для классов, замкнутых относительно Фреше-степеней, равносильно свойству отсутствия свойства DOP (Палютин-Старченко). Таким образом, указанный выше результат для суперстабильных теорий был получен в конце 80-х годов прошлого столетия. Переход от суперстабильного случая к стабильному является принципиальным.
Палютин Е. А. Простые модели над нормальным базисным множеством, Сиб. электрон. матем. изв., 2007, 4, 596-604.
Палютин Е. А. Стабильные теории Фреше-степеней, Сиб. электрон. матем. известия, 2008, Т. 5 С. 699-707.
Палютин Е. А. Элиминация кванторов в фреше-замкнутых классах без интерпретации графов, Труды Международной научной конференции "Современные проблемы математики, информатики и управления" г. Алматы, 2008, стр. 469.
Palyutin E. A. Non-commutative stable theories of Freshe-power are non-classificable, Алгебра и теория моделей, 7. Сборник трудов (Под ред. А. Г. Пинуса и С. В. Судоплатова). Новосибирск: изд-во НГТУ, 2009, 60-84.
Палютин Е. А. Интерпретация графов в некоммутативных теориях Фреше-степеней, Фундаментальная и прикладная математика, 2009, т. 15, N 5, С. 201-225.
Международная конференция «Мальцевские чтения», Институт математики им. С. Л. Соболева СО РАН Новосибирск, 19-23 ноября 2008 г.
Международная школа-семинар «Новые алгебро-логические методы решения систем уравнений в алгебраических системах», Омск, 16-22 августа 2009 г.
Международная научная конференция «Вычислимость и модели», Восточно-Казахстанский государственный технический университет им. Д. Серикбаева, Усть-Каменогорск, Казахстан, 30 августа – 1 сентября 2009 г.
6. Доказано, что конечная простая группа и группа, имеющие одинаковый порядок и множество порядков элементов, изоморфны.
Спектром группы называется множество порядков ее элементов. В 1987 году В. Ши высказал гипотезу о том, что каждая конечная простая группа однозначно с точностью до изоморфизма характеризуется в классе всех конечных групп ее спектром и порядком. В 1992 году вопрос о справедливости гипотезы Ши был включен в «Коуровскую тетрадь» (вопрос 12.39). Получен положительный ответ на этот вопрос, а именно доказано, что конечная простая группа и группа, имеющие одинаковый порядок и спектр, изоморфны.
Васильев А. В., Гречкосеева М. А., Мазуров В. Д. О конечных группах, изоспектральных простым симплектическим и ортогональным группам // Сиб. мат. журн. 2009. Т. 50, №6. С. 1223-1245.
Васильев А. В., Гречкосеева М. А., Мазуров В. Д. Характеризация конечных простых групп их спектром и порядком // Алгебра и логика. 2009. Т. 49, №6.
7. Доказана нётеровость по уравнениям произвольной жесткой разрешимой группы. Описаны координатные группы неприводимых алгебраических множеств над делимыми распавшимися жесткими группами.
Исследования относятся к области алгебраической геометрии над разрешимыми группами. Группа G жесткая, если в ней существует конечный нормальный ряд, факторы которого Gi/Gi+1 абелевы и, рассматриваемые как правые Z[G/Gi]-модули, не имеют модульного кручения. Оказывается, такой ряд определяется группой G однозначно. Важными примерами жестких групп являются свободные разрешимые группы. Жесткая группа называется делимой, если элементы фактора Gi/Gi+1 делятся на ненулевые элементы кольца Z[G/Gi] или, другими словами, Gi/Gi+1 является векторным пространством над телом частных этого кольца. Жесткая группа называется распавшейся, если она распадается в полупрямое произведение абелевых групп, изоморфных соответствующим факторам жесткого ряда. Распавшаяся делимая жесткая группа определяется однозначно мощностями баз соответствующих векторных пространств. Доказана нётеровость по уравнениям всех жестких групп и установлено, что произвольная жесткая группа вкладывается в подходящую делимую распавшуюся жесткую группу. Изучены свойства делимых жестких групп. Получены важные сведения непосредственно об алгебраической геометрии над делимой распавшейся жесткой группой M, а именно характеризуются неприводимые алгебраические множества на языке координатных групп этих множеств, а также на языке уравнений, описываются группы, универсально эквивалентные над M.
Романовский Н. С. «Делимые жесткие группы», Алгебра и логика, т.47, № 6, 2008, 762-776.
Романовский Н. С. «Нетеровость по уравнениям жестких разрешимых групп», Алгебра и логика, т.48, № 2, 2009, 258-279.
Романовский Н. С. «Неприводимые алгебраические множества над распавшимися делимыми жесткими группами», Алгебра и логика, т.48, № 6, 2009, 721-747.
8. Получено описание спектров всех конечных простых классических групп.
Спектром ω(G) конечной группы G называется множество порядков ее элементов. Спектр замкнут относительно взятия делителей, т.е. если число n лежит в ω(G), то все его делители также лежат в ω(G). Обозначим через μ(G) множество максимальных по делимости элементов из ω(G). Таким образом, если ν(G) – некоторое подмножество спектра группы G, для которого выполнены включения μ(G) ν(G) ν(G) ω(G), то ω(G) определяется по ν(G) однозначно и состоит из всех делителей чисел из ν(G). Для каждой конечной простой классической группы G построено множество ν(G) такое, что μ(G) ω(G), то ω(G) определяется по ν(G) однозначно и состоит из всех делителей чисел из ν(G). Для каждой конечной простой классической группы G построено множество ν(G) такое, что μ(G) ν(G) ν(G) ω(G). ω(G).
Бутурлакин А. А., Гречкосеева А. А. Циклическое строение максимальных торов в конечных классических группах // Алгебра и логика. 2007. Т. 46, № 2. C. 129-156.
Бутурлакин А. А. Спектры конечных линейных и унитарных групп // Алгебра и логика. 2008. Т. 47, № 2. C. 157-173.
Бутурлакин А. А. Спектры конечных классических групп и изоспектральные простые группы // ИМ СО РАН. 2009. препринт № 232.
Бутурлакин А. А. Спектры конечных симплектических и ортогональных групп // Мат. труды (в печати).
9. Разработан новый метод нахождения сферических структур на узлах и зацеплениях, и дано их описание.
Изучение сферических структур на трехмерных многообразиях или, в более общей постановке, на многообразиях с особенностями стало предметом исследований многих авторов в связи с положительным решением проблемы геометризации Терстона и, как следствие, гипотезы Пуанкаре. Важным классом трехмерных многообразий с особенностями являются трехмерные сферы, сингулярные множества которых – узлы или зацепления. Возникает проблема существования геометрических структур на указанном классе многообразий. Для гиперболического случая, она принципиально решена в работах У. Терстона. Существование евклидовых структур изучено в работах Дж. Порти, М. Боле, Х. Вайсса и других авторов. Сферический случай представляется наиболее интересным и наименее изученным. В настоящей работе предложен новый метод для нахождения сферических структур на узлах и зацеплениях. Он основан на введении переменной метрики в четырехмерном проективном пространстве. Коэффициенты метрики определяются в зависимости от строения фундаментальной группы узла и во многих важных случаях могут быть выписаны в явном виде. В частности, это справедливо для торических узлов и зацеплений, для которых установлены теоремы существования сферической структуры и явно вычислены соответствующие сферические объемы.
Колпаков А. А., Медных А. Д. Сферические структуры на торических узлах и зацеплениях // Сиб. мат. журн. 2009. Т. 50, N 5, С. 1083-1096.
10. Решена известная проблема Зейделя об объёмах неевклидовых тетраэдров.
В 1986 году Дж. Зейдель сформулировал гипотезу о том, что объем идеального гиперболического тетраэдра можно выразить как функцию от определителя и перманента его матрицы Грама. Несмотря на то, что явная формула для объема указанного тетраэдра известна со времен Лобачевского, проблема долго не поддавалась решению. Десятью годами позже, американские математики И. Ривин и Ф. Лю высказали более сильную гипотезу утверждающую, что объем произвольного неевклидова тетраэдра является функцией определителя его матрицы Грама. В настоящей работе показанно, что обе проблемы, в общем случае, решаются отрицательно. При этом установлено, что в классах остроугольных и тупоугольных идеальных тетраэдров проблема Зейделя имеет положительное решение.
Абросимов Н. В. К решению проблемы Зейделя об объемах неевклидовых тетраэдров // Сиб. электрон. мат. изв. 2009. Т. 6. С. 211-218.
11. Даны описания Парето-оптимальных решений многоцелевых задач выпуклой геометрии.
Рассмотрен новый класс экстремальных задач выпуклой геометрии, в которых требуется добиться наилучшего результата при наличии противоречивых целей, например, при заданной площади поверхности
выпуклой фигуры максимизировать ее объем и минимизировать толщину. Эти задачи трактуются в духе теории многокритериального принятия решений. Даны описания Парето-оптимальных решений векторных задач изопериметрического типа на основе техники пространства выпуклых множеств, линейной мажоризации и смешанных объемов. В качестве модельных примеров даны явные решения задач Урысона, усложненных условием уплощения в заданном направлении или требованием оптимизации выпуклой оболочки нескольких фигур.
Кутателадзе С. С. Многоцелевые задачи выпуклой геометрии // Сибирский мат. журн. 2009. Т. 50, № 5. С. 1123-1136.
12. Найдено достаточное условие представимости лоренцевых групп голономии глобально гиперболическими многообразиями.
Классификация групп голономии псевдо-римановых многообразий до сих пор не является завершенной, что связано с существованием приводимых неразложимых групп голономии. В лоренцевом случае список групп голономии известен, но каждая из них реализована только локально, т.е. лоренцевым многообразием, метрика на котором определена лишь в некоторой малой окрестности. В работе большая часть групп голономии (за исключением тех, ортогональная часть которых содержит слагаемое из конечного списка групп изотропии кэлеровых симметрических пространств) реализована глобально гиперболическими пространствами – пространствами, обладающими наиболее сильными свойствами причинности, имеющими право рассматриваться как аналог полных многообразий в лоренцевом случае.
Базайкин Я. В. Глобально гиперболические пространства со специальными группами голономии // Сибирский математический журнал. 2009. Том 50, № 4. С. 721-736.
13. Доказаны теоремы единственности восстановления слабо выпуклых тел по формам их круговых проекций, получены соответствующие оценки устойчивости. Установлены достаточные условия выпуклости плоской фигуры, однозначно определяемой двумя своими выпуклыми томографическими проекциями.
1. Построены и изучены классы ε-выпуклых и (k,ε)-выпуклых тел, расширяющие класс выпуклых тел. Тела из этих расширенных классов представимы в виде дополнений к объединениям шаров радиуса 1/ε и, соответственно – цилиндров с k-мерными образующими и радиусами 1/ε. Изучены также некоторые модификации классов ε-выпуклых и (k,ε)-выпуклых тел, для некоторых из них доказаны аналоги классических теорем о выпуклых тел (теорема Хелли) и ряд результатов, относящихся к одному из важнейших вопросов геометрической томографии: Если проекции двух тел A и B на все плоскости из некоторого набора плоскостей конгруентны относительно некоторой группы преобразований G, будут ли тела A и B конгруентны относительно некоторой (другой) группы преобразований объемлющего пространства? Для случая круговых проекций и для ε-выпуклых тел доказаны теоремы единственности и получены соответствующие оценки устойчивости.
2. Пусть M – измеримое ограниченное множество на плоскости и F(x), G(y) – томографические проекции ее характеристической функции. Пусть F(x) и G(y) выпуклы, а их невозрастающие перестановки y=f(x), x=g(y) являются взаимно-обратными функциями. (Это условие эквивалентно единственности решения обратной задачи восстановления множества M по функциям F(x) и G(y)). Установлены условия на эти проекционные данные, достаточные для выпуклости восстанавливаемого множества M. Отметим, что для любого конечного набора направлений на плоскости можно построить невыпуклый многоугольник, у которого томографические проекции в этих направлениях выпуклы. Это показывает существенность условия на перестановки функций F, G. Указаны возможные многомерные обобщения этой теоремы.
СМЖ (в соавторстве с В. Ю. Ровенским), т.50, N 5, 2009, с. 1037-1049. SibAM, V. 19, N 2, 2009, 85-90.
14. Доказано существование однородной нильпотентной аппроксимации для C1-гладких векторных полей.
В некоторой окрестности O евклидова пространства RN рассматривается набор C1 –гладких базисных канонических векторных полей X1 ,…, XN , т.е. набор таких полей, что в каждой точке x из O они линейно независимы, и для любого векторного поля вида a1X1 +…+ aNXN, где все ai – достаточно малые по модулю константы, его интегральная линия является обычной прямой линией с направляющим вектором (a1,…, aN), исходящей из начала координат. Предположим, что рассматриваемые векторные поля таковы, что им соответствуют некоторые натуральные числа deg Xi (их степени), deg X1=1, образующие неубывающую последовательность, и коммутатор любых двух векторных полей самое большее может только складывать их степени в таблице коммутаторов. Пусть δτ(x)=(τdeg X1x1,…, τdeg XNxN) – неоднородный оператор растяжения, индуцированный в O степенями векторных полей. В этом случае, используя некоторые методы дифференциальных уравнений и теории групп Ли, нами доказано, что найдется некоторая окрестность начала координат B, принадлежащая O, размеры которой контролируются вдоль соответствующих координатных осей числами deg Xi , такая, что под действием оператора δ1/τ векторные поля τdeg Xi Xi , определенные на δτB, равномерно сходятся к некоторым векторным полям на B, и «предельные» векторные поля при некоторых условиях образуют нильпотентную алгебру Ли на В. Используя полученный результат, нами установлены некоторые результаты, связанные с существованием квазиметрик на C2-гладких пространствах Карно – Каратеодори. Также, в рамках используемого метода доказательства, нами исследованы вопросы, связанные с ослаблением условий гладкости на векторные поля X1 ,…, XN.
Грешнов А. В. О применении методов группового анализа дифференциальных уравнений для некоторых систем C1-гладких векторных полей // Сиб. Мат. журн. 2009. Т. 50, № 1. С. 47-62.
15. Найдены необходимые и достаточные условия однозначной определённости областей в евклидовых пространствах относительной метрикой границы, индуцированной внутренней метрикой области.
Относительная метрика на границе области определяется как продолжение по непрерывности внутренней метрики области U. (Напомним, что расстояние по внутренней метрике области U между точками x,y U равно инфимуму длин кривых, лежащих в U и соединяющих x,y.) Чтобы такое продолжение сделать возможным и в случае нерегулярных областей, вводится понятие хаусдорфовой границы, которую можно получить, пополнив область U по Хаусдорфу относительно внутренней метрики и удалив из полученного пополнения точки самой области. Предположим, что хаусдорфовы границы областей изометричны в относительных метриках. Требуется выяснить, в каком случае сами области будут конгруэнтными. Эта задача включает в себя как частный случай классическую задачу об однозначной определенности выпуклых поверхностей их внутренней метрикой, решенную А.В. Погореловым. U равно инфимуму длин кривых, лежащих в U и соединяющих x,y.) Чтобы такое продолжение сделать возможным и в случае нерегулярных областей, вводится понятие хаусдорфовой границы, которую можно получить, пополнив область U по Хаусдорфу относительно внутренней метрики и удалив из полученного пополнения точки самой области. Предположим, что хаусдорфовы границы областей изометричны в относительных метриках. Требуется выяснить, в каком случае сами области будут конгруэнтными. Эта задача включает в себя как частный случай классическую задачу об однозначной определенности выпуклых поверхностей их внутренней метрикой, решенную А.В. Погореловым.
В работе сформулированы необходимые и достаточные условия на область, чтобы она однозначно определялась относительной метрикой своей хаусдорфовой границы. При этом на области не налагается никаких априорных предположений о гладкости. Доказано, в частности, что каждая область с ограниченной границей в евклидовом пространстве размерности 3 и выше однозначно определяется указанной метрикой границы.
Коробков М. В. Критерий однозначной определенности областей в евклидовых пространствах метрикой границы, индуцированной внутренней метрикой области // Математические труды, 2009, Т.12, No.2, С.52--96.
16. На линейном уровне исследована задача об обтекании бесконечного плоского клина сверхзвуковым стационарным потоком газа. Доказана асимптотическая устойчивость по Ляпунову стационарного решения в случае слабой ударной волны для финитных начальных данных. Тем самым дано обоснование известной гипотезы Куранта-Фридрихса.
Полученный результат – вклад в объяснение ставшего уже классическим физического парадокса. Как известно, задача об обтекании равномерным сверхзвуковым потоком невязкого, нетеплопроводного газа бесконечного плоского клина (величина угла при вершине клина меньше критического значения) имеет два решения: одно отвечает сильной ударной волне (течение за ударной волной - дозвуковое), а второе – слабой ударной волне (течение за ударной волной, вообще говоря, сверхзвуковое) [R. Courant, K. O. Friedrichs, Supersonic flow and shock waves, N. Y., Interscience Publishers, 1948]. Удивительно, но если специальным образом не управлять физическим экспериментом или проведением численных расчетов [M. D. Salas, B. D. Morgan, AIAA J.,1983, V. Elling, T.-P. Liu, Proceedings of the “Eleventh International Conference on Hyperbolic Problems. Theory, Numerics, Applications”, Lyon, 2007], то реализуется решение со слабой ударной волной. Таков результат многочисленных экспериментов. Однако, строгого математического объяснения, почему это происходит, до недавнего времени не было.
Более того, как отмечают в своих недавних исследованиях T.-P. Liu и V. Elling, физические и численные эксперименты имеют ряд существенных недостатков, например: 1) влияние внешних эффектов таких, как физическая и численная диссипация, кинетические эффекты; других аномальных свойств решений; 2) эти методы не пригодны для исследования неустойчивых решений, или решений, близких к неустойчивым. Следовательно, в данном конкретном эксперименте нельзя достоверно утверждать, что реализуется тот или иной режим. В середине XX столетия R. Courant и K. O. Friedrichs высказали гипотезу о том, что, вероятно, решение, отвечающее сильной ударной волне с возрастанием времени неустойчиво (по Ляпунову), а решение, соответствующее слабой ударной волне, напротив, устойчиво. Причем это справедливо уже в случае соответствующей линейной задачи. В работах авторов эта гипотеза получила полное подтверждение [A. M. Blokhin, D. L. Tkachev, L. O. Baldan, Study of the stability in the problem on flowing around a wedge. The case of strong wave, J. Math. Anal. Appl., 319 (2006); A. M. Blokhin, D. L. Tkachev, Yu. Yu. Pashinin, Stability condition for strong shock waves in the problem of flow around an infinite plane wedge, Nonlinear Analysis: 2(2008)] в части обоснования неустойчивости сильной ударной волны. Кратко суть дела такова: даже в случае финитных начальных данных с ростом времени возмущение, приходя в вершину клина, разрушает решение. Такое поведение решения объясняется появлением в асимптотическом разложении решения в окрестности вершины клина слагаемого, содержащего отрицательную степень расстояния точки до вершины. Единственный, к сожалению, в большей степени теоретический способ уничтожить это возмущение – наложить на начальные данные дополнительные интегральные условия.
Случай слабой ударной волны кардинально отличается от уже описанного тем, что после преобразования Лапласа возникает не эллиптическая, а гиперболическая задача, а значит, нужно использовать совершенно другие методы.
Отметим определенную завершенность исследования соответствующей линейной смешанной задачи в случае, когда основное решение отвечает слабой ударной волне (течение за ударной волной - сверхзвуковое). Именно, получены следующие результаты. 1) Найдено представление классического решения линейной смешанной задачи в явном виде. 2) В случае финитных начальных данных обоснована асимптотическая устойчивость по Ляпунову стационарного решения.
Блохин А. М., Ткачев Д. Л. Устойчивость сверхзвукового обтекания клина со слабой ударной волной // Мат. сборник, 2009, 200, №2, 3-30
Blokhin A. M, Tkachev D. L. Justification of the Courant-Friedrich’s hypothesis in the case of a weak shock. Part I. Presentation of solution to linear problem // Mathematical Analysis and Applications, 2009, Vol. 355. Pp.41-52.
17. Доказана локальная по времени теорема существования и единственности в пространствах Соболева для уравнений газовой динамики с нулевым давлением на свободной границе "газ-вакуум" при условии, что плотность газа строго положительна на этой границе в начальный момент времени.
Рассматривается задача со свободной границей для уравнений газовой динамики в трехмерном случае в области со свободной границей F(t,x)=0 с граничными условиями dF/dt = 0 и p = 0, где p - давление газа, а d/dt - субстанциональная производная. То есть на границе, движущейся со скоростью частиц газа, давление равно нулю, что описывает движение идеальной сжимаемой жидкости в вакууме. Эта задача часто используется для моделирования движения океана или газообразной звезды. При моделировании движения газообразной звезды важно также учитывать релятивистские эффекты. Недавно локальная по времени корректность указанной задачи была доказана в работе Lindblad'а (2005) для изэнтропических нерелятивистских уравнений газовой динамики для случая жидкости, т.е. в предположении, что плотность газа строго положительна на этой границе в начальный момент времени. Автором результата предложен новый подход к исследованию задачи, который не предполагает переход к Лагранжевым координатам. Этот подход позволил без труда распространить результат Lindblad'а не только на полную систему газовой динамики, но и на релятивистский случай (в рамках частной теории относительности). Таким образом, доказана локальная по времени теорема существования и единственности в пространствах Соболева для уравнений газовой динамики с граничным условием p=0 на свободной границе "газ-вакуум" при условии, что плотность газа строго положительна на этой границе в начальный момент времени. Аналогичная теорема доказана для уравнений релятивистской газовой динамики в рамках частной теории относительности.
Trakhinin Y. Local existence for the free boundary problem for nonrelativistic and relativistic compressible Euler equations with a vacuum boundary condition. Comm. Pure Appl. Math. 62 (2009), 1551-1594.
18. Найдена аппроксимация для распределений, возникающих при изучении так называемых переходных явлений для случайных блужданий, порожденных суммами случайных величин, не имеющих математических ожиданий. Ранее аналогичные задачи исследовались лишь для конечных математических ожиданий. Полученные результаты позволяют найти асимптотику распределения времени ожидания в нагруженных системах обслуживания, у которых времена обслуживания имеют медленно убывающие на бесконечности распределения.
В работе изучаются так называемые переходные явления для сумм независимых случайных величин, не имеющих среднего. Под переходными явлениями для случайных величин, имеющих среднее, обычно понимают предельное поведение максимума частичных сумм случайных величин, когда математические ожидания слагаемых отрицательны и стремятся к нулю. В этом случае рассматриваемый максимум, как правило, сходится по вероятности к бесконечности. Распределение максимума, как известно, является предельным распределением времени ожидания обслуживания в одноканальных системах. Если этот максимум неограниченно возрастает, то рассматриваемая модель соответствует работе системы обслуживания в условиях большой нагрузки. Исследования переходных явлений в условиях, когда слагаемые не имеют среднего, в литературе до сих пор не рассматривалась, однако эта ситуация встречается в конкретных приложениях, и здесь требуется совсем другая постановка задачи о переходных явлениях. Например, можно предположить, что каждое слагаемое есть разность двух независимых случайных величин из областей притяжения соответствующих устойчивых распределений. Распределения слагаемых ведут себя таким образом, что рассматриваемый максимум сходится по вероятности к бесконечности. В работе получено предельное распределение максимума подобных частичных сумм при соответствующей нормировке. Рассмотрены случаи одинаково распределенных и разнораспределенных слагаемых.
А. А. Боровков, П. С. Рузанкин Переходные явления для случайных блужданий при отсутствии математического ожидания скачков. Сибирский математический журнал, 2009, т. 50, № 5, с. 987-1009.
19. Установлен ряд базовых свойств распределений, медленно убывающих на бесконечности. Эти распределения играют существенную роль при изучении стохастических моделей систем обслуживания и коммуникационных систем.
Представляемый цикл работ посвящен исследованию распределений, которые характеризуются прежде всего медленным убыванием на бесконечности.
В рамках этого цикла получено окончательное решение задачи о возможной константе в определении субэкспоненциальных распределений. Подход к доказательству основан на исследовании нижнего предела отношения хвостов свертки и исходного распределения. Получен фундаментальный результат, что для любого распределения на положительной полуоси с тяжелым хвостом нижний предел всегда равен 2. Тем самым усилен результат Б. А. Рогозина (2000), доказавшего этот факт для распределений с асимптотически плоскими хвостами.
Результаты о нижней грани отношения хвоста двойной свертки к хвосту исходного распределения обобщены на свертку случайного числа неотрицательных слагаемых, или, что эквивалентно, на распределение суммы, остановленной в случайный независимый момент времени. Доказано, что для любого распределения с тяжелым хвостом нижняя грань этого отношения равна среднему значению числа слагаемых при условии, что число слагаемых обладает некоторым конечным экспоненциальным моментом. Получены
уточняющие следствия для распределений, не все моменты которых конечны. Доказаны следствия для сложного пуассоновского распределения, устойчивых законов, для супремума случайного блуждания, обобщающие результаты Embrechts, Goldie & Veraverbeke (1979), Pakes (2004), Shimura & Watanabe (2005). Кроме того, получены общие окончательные условия на независимый момент остановки, при которых нижний предел равен среднему числу слагаемых.
Исследовано асимптотическое поведение вероятностей больших уклонений суммы независимых одинаково распределенных случайных величин, остановленной в случайный момент времени. Изучается случай тяжелых хвостов. Обобщены и дополнены результаты Greenwood & Monroe (1973, 1977), Stam (1973), Daley, Omey & Vesilo (2007), А. А. Боровкова & К. А. Боровкова (2008), Боровкова & Утева (1993), Шнеера (2004).
S. Foss, D. Korshunov. Lower limits and equivalences for convolution tails. The Annals of Probability, 2007, V. 35, P. 366-383.
Д. Денисов, Д. Коршунов, С. Фосс. Нижние пределы для хвостов распределений случайно остановленных сумм. Теория вероятностей и ее применения, 2007, Т. 52, С. 794-802.
D. Denisov, S. Foss, D. Korshunov. On lower limits and equivalences for distribution tails of randomly stopped sums. Bernoulli, 2008, V. 14, P. 391-404.
D. Denisov, S. Foss, D. Korshunov. Asymptotics of randomly stopped sums in the presence of heavy tails. Accepted to "Bernoulli".
20. Получены новые оценки скорости сходимости градиентных методов решения обратных и некорректных задач.
Новые оценки скорости сходимости получены с использованием оценок условной устойчивости некорректных задач. При этом показано, что основную роль в оценках скорости сходимости играет степень некорректности задачи. До настоящего времени существовало несколько способов определения степени некорректности задачи Aq=f, где q – искомое решение, f – данные задачи, а A – оператор, который в большинстве обратных и некорректных задач является компактным оператором. Первый, наиболее общий и естественный способ, заключается во введении модуля непрерывности обратного оператора. Однако, явное выражение для модуля непрерывности в конкретных случаях не всегда возможно, поэтому, чаще всего для конкретных задач исследователи пытаются найти оценки условной устойчивости, которые также характеризуют степень некорректности задачи. С. И. Кабанихиным показано [1], что оценка условной устойчивости позволяет получить оценку скорости сильной сходимости градиентных методов. При этом основным вопросом при исследовании обратных задач и численных методов решения оставался метод получения конкретных оценок условной устойчивости.
Более детальное исследование данного вопроса показало, что оценка условной устойчивости может быть получена при условии достаточной гладкости искомого решения на основе теоремы о сингулярном разложении компактного оператора. Показано [2-4], что степень стремления к нулю последовательности сингулярных чисел компактного оператора А является характеристикой степени некорректности задачи Aq=f. Чем быстрее сходится к нулю последовательность сингулярных чисел, тем более некорректной является задача. Вторым важным преимуществом данного подхода является возможность применения к некорректным задачам линейной алгебры (системы линейных алгебраических уравнений с прямоугольными, вырожденными или плохо обусловленными матрицами). Метод, предложенный С. К. Годуновым, дает исчерпывающий ответ на вопрос о том, какую полезную информацию о решении некорректной задачи можно извлечь с гарантированной точностью из данных задачи f c учетом уровня ошибок измерений. В случае, когда размеры системы слишком велики для непосредственного применения сингулярного разложения, поведение последовательности сингулярных чисел позволяет получить оценки скорости сходимости градиентных методов решения и, кроме того, позволяет получить правило нахождения номера итерации, на которой следует остановить вычисления [4, глава 2, теорема 2.8.1].
Kabanikhin S. I. Conditional stability stopping rule for gradient methods applied to inverse and ill-posed problems. // J. of Inverse and Ill-Posed Problems, 2006. 14(8), 805-812.
Kabanikhin S. I. Definitions and Examples of Inverse and Ill-Posed Problems. // J. Inv. Ill-Posed Problems. 2008. 16(4), 317-357.
Kabanikhin S. I. and Schieck M. Impact of conditional stability: сonvergence rates for general linear regularization methods // J. Inv. Ill-Posed Problems. 2008. 16(3), 267-282.
Кабанихин С. И. Обратные и некорректные задачи. Сибирское научное издательство, 2009. 450 с. (второе издание).
21. Разработан метод оптимального по быстродействию управления в реальном времени линейными системами с возмущениями.
В цикле работ разработан метод оптимального по быстродействию управления в реальном времени линейными системами с возмущениями. Предложен способ формирования в реальном времени кусочно-постоянного финитного управления, переводящего за фиксированное время линейную систему из любого начального состояния в начало координат и дающего приближенное решение задачи быстродействия. Получена система линейных алгебраических уравнений, связывающая отклонения фазовых координат с отклонениями начальных условий нормированной сопряженной системы и с отклонением конечного момента времени. Полученные соотношения позволяют преобразовать последовательность финитных управлений в оптимальное по быстродействию управление. Вычисления сводятся к последовательности решений систем линейных алгебраических уравнений и интегрированию матричного дифференциального уравнения на интервалах перемещения конечного момента времени и моментов переключений управления. Предложен способ задания начального приближения, значительно уменьшающий вычислительную трудоемкость. Доказана локальная сходимость с квадратичной скоростью и глобальная сходимость последовательности управлений к оптимальному по быстродействию управлению. Получены простые конструктивные условия возникновения скользящего режима, движения изображающей точки по многообразиям переключений и изменения структуры оптимального управления при сопровождении фазовой траектории движения системы с возмущением. Доказано, что если не учитывать возмущение в алгоритме управления, то фазовое состояние линейной динамической системы при одновременном действии возмущения и оптимального управления переводится в состояние динамического равновесия. Исследовано влияние различных параметров на положение точки динамического равновесия и форму предельного цикла. Приведены итерационный вычислительный алгоритм, результаты моделирования и численных расчетов.
Александров В. М. Последовательный синтез оптимального по быстродействию управления в реальном времени // Автоматика и телемеханика. 2008. № 8. С. 2-24.
Александров В. М. Последовательный синтез оптимального по быстродействию управления линейными системами с возмущениями // Сибирский журнал вычислительной математики. 2008. Т. 11, № 3. С. 251-270.
Александров В. М. Оптимальное по быстродействию управление в реальном времени линейными системами с возмущениями // Вестник НГУ. Серия: математика, механика, информатика. 2008. Т. 8, вып. 3. С. 3-25.
Александров В. М. Особенности движения динамических систем с возмущениями в окрестности многообразий переключений // Автоматика и телемеханика. 2009. № 4. С. 58-77.
Александров В. М. Численный метод решения линейной задачи минимизации расхода ресурсов // Сибирский журнал вычислительной математики. 2009. Т. 12, № 3. С. 247-267.
Александров В. М. Оптимальное по быстродействию позиционно-программное управление линейными динамическими системами // Сибирские электронные математические известия. 2009. Т. 6. С. 385-439.
22. Найдена аксиоматизация обобщенного расширения Оуэна, как для конечных, так и для широкого класса бесконечных игр. Установлено, что для неатомических игр такая аксиоматизация совпадает с описанием мультипликативного продолжения Аумана-Шепли.
Предлагается новый подход к построению обобщенного расширения Оуэна для игр с бесконечным числом участников, основанный на методах неаддитивного интегрирования. Эти методы конкретизируют идеи v-интегрируемости, разработанные в более ранних работах автора. Помимо построения и анализа ряда конструкций продолжения, включая описание строения симметрических степеней борелевской алгебры метрического компакта, большое внимание уделяется различным аспектам аксиоматизации отображения, сопоставляющего играм их обобщенные расширения Оуэна. Один из главных результатов работы показывает, что в качестве искомой аксиоматизации для широкого класса неатомических игр можно использовать, с точностью до технических деталей, характеризацию известного мультипликативного продолжения Аумана-Шепли. Таким образом, впервые дано явное, конструктивное описание указанного мультипликативного продолжения, представляющее большой теоретический и практический интерес. Это описание, вместе с бесконечномерным аналогом известного интегрального представления Оуэна, может эффективно использоваться как для численного отыскания вектора Шепли, так и для теоретического анализа взаимосвязи полярных форм и дележей Шепли неатомических игр. Что касается конечных кооперативных игр, где классическое расширение Оуэна трактуется как математическое ожидание выигрыша коалиции в игре с независимым стохастическим поведением участников, то и для этого класса впервые найдена аксиоматизация соответствующего отображения. Оказалось, что единственным принципиальным отличием от неатомического случая является частичное нарушение мультипликативности: расширение Оуэна произведения двух конечных игр равно произведению расширений сомножителей лишь при условии дизъюнктности минимальных носителей этих игр.
Васильев В. А. Об одной аксиоматизации обобщенного расширения Оуэна. «Математическая Теория Игр и её Приложения», 2009, т.1, в.2, с. 3 - 13.
23. Разработаны и исследованы модели для поиска оптимальной маркетинговой политики. Изучен специальный класс задач дробного оптимального управления, возникающих при анализе модели максимизации эффективности рекламных затрат.
Разработаны модели для поиска оптимальной маркетинговой политики.
Исследована нелинейная модель оптимизации стимулирования (оптового дисконта) фирмой-производителем ритейлера (посредника). Учет специфики задачи позволил описать структуру оптимального решения. Установлен характер зависимости вида оптимальной стратегии производителя по формированию оптовой цены от поведения ритейлера при определении розничной цены. В частности, доказано, что возрастание оптового дисконта оптимально для стимулирования «неэффективного» ритейлера; в случае же эффективного ритейлера возможно повышение розничной цены в конце периода продаж. (Совместно с С. Вианелло, Е. Моретти, А. Эллеро.)
Изучен специальный класс задач дробного оптимального управления с линейной динамикой и целевым функционалом, являющимся отношением двух интегралов. Для таких задач непосредственное применение стандартной техники оптимального управления невозможно. Использование линеаризации (известное в западной литературе как подход Динкельбаха для дробного программирования) позволило свести исходную задачу к однопараметрическому семейству задач линейного оптимального управления. Обнаруженная дифференцируемость вспомогательной функции параметра позволила провести анализ чувствительности оптимального решения к изменению входных данных. Полученные результаты применены к анализу модели максимизации эффективности рекламных затрат. (Совместно с Е. Моретти, С. Фунари, А. Эллеро.).
Bykadorov I., Ellero A., Moretti E., Vianello S. “The role of retailer’s performance in optimal wholesale price discount poli-cies.” - European Journal of Operational Research, 2009, vol. 194, no. 2, p. 538–550.
Bykadorov I., Ellero A., Funari S., Moretti E. “Dinkelbach Approach to Solving a Class of Fractional Optimal Control Prob-lems.” – Journal of Optimization Theory and Applications, 2009, vol. 142, no. 1, p. 55–66.
24. Получены новые верхние оценки хроматического числа в задачах игровой раскраски, реберного разложения на лес и подграф для нескольких классов разреженных плоских графов. Опровергнута известная гипотеза (2002) о разбиении ребер плоского графа.
Игровая раскраска графа служит моделью более общей ситуации противоборства при оценке параметров дискретного объекта. Недавно обнаруженным средством получения верхних оценок для игрового хроматического числа χg(G) графа G служит разбиение ребер графа G на лес (подграф без циклов) и подграф максимальной степени не больше k (это свойство обозначим через FMk). В свою очередь, FMk сразу вытекает из существования в разреженных (в том или ином смысле) плоских графах ребра высоты не более k+1 (данное свойство обозначим Hk). Для нескольких классов разреженных плоских графов получен ряд результатов по трем указанным задачам, усиливающих ранее известные зарубежные результаты. В частности, доказано, что любой С4-свободный плоский граф G обладает свойствами H7 (и найдена конструкция, подтверждающая неулучшаемость этого результата), FM6 и χg(G) ≤ 10, а если, более того, его обхват (длина кратчайшего цикла) не менее 9, то он обладает свойствами FM1 и χg(G) ≤ 5. С другой стороны, опровергнута гипотеза Хи, Ху, Ли, Шао, Ванга и Жу (2002) о разбиении ребер произвольного плоского графа G на лес и подграф степени не более ⌈∆(G)/2⌉+1, где ∆(G) – максимальная степень графа G.
O. V. Borodin, A. O. Ivanova, B. S. Stechkin. Decomposing a planar graph into a forest and a subgraph of restricted maximum degree, Siberian Electronic Math. Reports 4 (2007). 296-299.
O .V. Borodin, A. O. Ivanova, A. V. Kostochka and N. N. Sheikh. , Minimax degrees of quasiplane graphs without 4-faces, Siberian Electronic Math. Reports 4 (2007) 435-439.
O. V. Borodin, A. V. Kostochka, N. N. Sheikh, and Gexin Yu. Decomposing a planar graph with girth nine into a forest and a matching, Europ. J. Combin., 29 (2008) 1235-1241.
O. V. Borodin, A. O. Ivanova, A. V. Kostochka, N. N. Sheikh. Minimax degrees of quasiplanar graphs without short cycles other than triangles, Taiwanese J. of Math. 12 (2008), no. 4, 873-886.
O. V. Borodin, A. V. Kostochka, N. N. Sheikh, and Gexin Yu. M-degrees of quadrangle-free planar graphs, J. of Graph Theory 60, 1, (2009) 80-85.
O. V. Borodin, A. O. Ivanova, A. V. Kostochka, N. N. Sheikh. Planar graphs decomposable into a forest and a matching, Discrete Math. 309 (2009) 277-279.
O. V. Borodin, A. O. Ivanova, A. V. Kostochka and N. N. Sheikh. Decompositions of quadrangle-free planar graphs, Discus. Math. Graph Theory 29 (2009) 87-99.
25. Доказано, что всякий двоичный код, исправляющий одну ошибку, может быть вложен в некоторый 1-совершенный код большей длины.
В каждой грани n-мерного двоичного куба, содержащего совершенный код с расстоянием 3, содержится некоторый код с тем же кодовым расстоянием, но уже не обязательно совершенный. Это может быть произвольная система троек Штейнера, оптимальный 1-код, или любой из известных кодов с большим кодовым расстоянием. Естественно возникающий при этом вопрос: «Нет ли каких-нибудь ограничений на коды, вложимые в совершенные?» является предметом нашего рассмотрения. Оказалось, что единственным таким ограничением является кодовое расстояние 3. Для доказательства использована техника одновременного сдвига непересекающихся компонент в кодах Хемминга.
S. V. Avgustinovich, D. S. Krotov. Embedding in a Perfect Code // J. Combin. Designs. 17(5) 2009, 419–423.
26. Построены несистематические совершенные коды над любым конечным полем.
Такие коды строятся из q-значного кода Хемминга 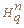 ,
n=(qn-1)/(q-1) сдвигами его непересекающихся i-компонент. Показано, что при
m≥4 минимальное число компонент, необходимое для построения несистематического кода, равно семи при q≠5,7 и равно восьми, если q=5 или 7. Доказано также, что при m=3 тоже существуют несистематические коды, если q не является простым числом (для простых q этот вопрос остался открытым). Для построения таких кодов применялись сдвиги так называемых минимальных (или простых) i-компонент кода Хемминга. ,
n=(qn-1)/(q-1) сдвигами его непересекающихся i-компонент. Показано, что при
m≥4 минимальное число компонент, необходимое для построения несистематического кода, равно семи при q≠5,7 и равно восьми, если q=5 или 7. Доказано также, что при m=3 тоже существуют несистематические коды, если q не является простым числом (для простых q этот вопрос остался открытым). Для построения таких кодов применялись сдвиги так называемых минимальных (или простых) i-компонент кода Хемминга.
Малюгин С. А. О несистематических совершенных кодах над конечными полями // Дискрет. анализ и исслед. опер, 2009. Т.16, N 1. C. 44-63.
27. Обоснован полиномиальный точный алгоритм с улучшенной на порядок временной сложностью для решения задачи размещения с одинаковыми производственными мощностями предприятий на путевом графе.
Задачи размещения составляют один из наиболее актуальных и широких разделов исследования операций. Их математический анализ в большинстве случаев приводит к рассмотрению труднорешаемых задач дискретной оптимизации. Значительные успехи в этой области к настоящему времени достигнуты в исследовании задач размещения с неограниченными производственными мощностями (Uncapacitated Facility Location Problem – UCFLP). Существенно более скромны достижения для задачи размещения с ограничениями на объемы производства предприятий (Capacitated Facility Location Problem – CFLP). В практических приложениях достаточно важной является метрическая задача размещения, когда расстояния между объектами (пунктами производства и потребления) удовлетворяют неравенству треугольника. Известно, что метрическая задача размещения на сети является NP-трудной, даже в случае неограниченных объемов производства. Авторы рассматривают подкласс метрических задач CFLP, в котором пункты производства и потребления расположены в вершинах путевого графа, а мощности предприятий одинаковы. До недавнего времени единственным полиномиальным точным алгоритмом для этого подкласса задач был предложенный одним из авторов алгоритм с временной сложностью O(m5n2+m3n3), где m и n – число предприятий и число пунктов спроса, соответственно. В представленном результате для решения задачи размещения на путевом графе с одинаковыми производственными мощностями приводится обоснование модифицированного полиномиального точного алгоритма с временной сложностью O(m4n2). Это на порядок улучшает ранее достигнутый результат как относительно числа предприятий, так и относительно количества потребителей.
А. А. Агеев, Э. Х. Гимади, А. А. Курочкин Полиномиальный алгоритм решения задачи размещения на цепи с одинаковыми ограничениями на объемы производства предприятий // Дискретный анализ и исследование операций. 2009. Т. 16, № 5, С. 3–18.
28. Получены структурные свойства оптимальных расписаний с прерываниями, позволившие обобщить большое число ранее известных результатов о сложности задач и закрывающие две ранее открытых проблемы о существовании оптимального расписания с конечным числом прерываний.
Такие результаты установлены для широкого круга моделей, включая как большинство классических, так и нетрадиционных моделей теории расписаний и календарного планирования с ресурсными ограничениями, а также – для широкого круга целевых функций, включая все классические. Кроме того, для достаточно общей расписательной модели и достаточно общих целевых функций получены две теоремы о рациональной структуре, согласно которым для любого примера с непустым множеством допустимых решений существует оптимальное расписание со следующими свойствами: (1) суммарное число прерываний не превосходит полинома от числа операций и от числа фиксированных дат, заданных на входе; (2) все точки переключения в расписании (т.е. моменты начала, завершения, прерывания и возобновления операций) совпадают с моментами времени, кратными некоторому рациональному числу д; при этом длина записи числа д ограничена полиномом от длины записи входа задачи; (3) оптимальное значение целевой функции является числом, кратным числу д, при этом длина записи коэффициента кратности также ограничена полиномом от длины записи входа. Важным следствием этих теорем о рациональной структуре является заключение о том, что распознавательные аналоги оптимизационных задач с прерываниями принадлежат классу NP.
Результат обобщает большое число известных ранее результатов о «редуцировании прерываний» в задачах с единичными длительностями, а также о сложности таких задач; он также закрывает две открытые проблемы о существовании оптимальных расписаний без прерываний в задачах минимизации суммарного взвешенного опоздания и взвешенного числа опоздавших работ на параллельных машинах с единичными работами, неодинаковыми временами их поступления в систему, ограничениями предшествования в виде цепей и разрешением прерываний.
Ph. Baptiste, J. Carlier, A. Kononov, M. Queyranne, S. Sevastyanov, and M. Sviridenko. Integrality Property in Preemptive Parallel Machine Scheduling, In: A.Frid a.o. (Eds.), Computer Science – Theory and Applications, 4th International Computer Science Symposium in Russia, CSA 2009, Novosibirsk, Russia, August 2009, Proceedings, Lecture Notes in Comp. Sci., 5675, Springer-Verlag, 2009, 38-46.
29. Установлена полиномиальная разрешимость задачи оптимальной рекомбинации в генетических алгоритмах для задач упаковки и разбиения множества, простейшей задачи размещения производства, а также задач булевого линейного программирования, имеющих не более двух переменных в каждом ограничении.
Рассмотрена оптимизационная задача, состоящая в отыскании наилучшего по целевой функции решения-потомка из множества всех возможных потомков на выходе оператора рекомбинации в генетическом алгоритме (ГА). Пара родительских решений при этом считается заданной. Оптимальная рекомбинация
исследуется в случае, когда решения задачи представляются бинарными векторами. С использованием эффективны сводимостей задач оптимальной рекомбинации нами установлена полиномиальная разрешимость подзадачи оптимальной рекомбинации для взвешенных задач упаковки и разбиения множества и простейшей задачи размещения производства, сформулированных как задачи булевого линейного программирования. Кроме того, показана полиномиальная разрешимость оптимальной рекомбинации на классе задач булевого линейного программирования, имеющих не более двух переменных в каждом ограничении. Установлена NP-трудность ряда задач оптимальной рекомбинации, в частности, задач булевого линейного программирования, имеющих три переменные в каждом ограничении, задач о рюкзаке, о покрытии множества и о p-медиане в формулировке булевого программирования. (Eremeev, 2008).
Проведены экспериментальные исследования операторов оптимальной рекомбинации, основанных на решении вспомогательных задач частично целочисленного линейного программирования. Для задачи управления поставками с ограничениями снизу на объем заказа разработано два варианта ГА (Borisovsky, Dolgui, Eremeev, 2009). В первом алгоритме используется двоичное представление решений и оператор оптимальной рекомбинации. Второй ГА основан на представлении решений с использованием перестановок и на "жадном" декодере. Проведенные эксперименты показали, что ГА с оператором оптимальной рекомбинации имеет преимущество в стоимости получаемых решений по сравнению со вторым ГА, а также по сравнению с коммерческим пакетом решения частично целочисленных задач CPLEX. Аналогичные результаты получены для задач балансировки производственной линии и составления расписаний (Еремеев, Коваленко, 2009), (Dolgui, Eremeev, Guschinskaya, 2008, 2010).
Borisovsky P., Dolgui A., Eremeev A. Genetic algorithms for a supply management problem: MIP-recombination vs greedy decoder // European Journal of Operational Research. Vol. 195 N 3, 2009, P. 770-779.
Dolgui A., Eremeev A. and Guschinskaya O. MIP-based GRASP and genetic algorithm for balancing transfer lines // In: Ma-theuristics. Hybridizing Meta-heuristics and Mathematical Programming / Maniezzo, V., Stutzle, T., Voss, S. (eds.) Series An-nals of Information Systems, Vol. 10, Springer, 2010, P. 189-208.
Dolgui A., Eremeev A., Guschinskaya O. MIP-based heuristics for scheduling batch production with shifts // Book of Abstracts of GOR Workshop "Scheduling in the Process Industry", Bad Honnef, Germany, 2008. P. 8.
Eremeev A. V. NP-hard cases of optimal recombination. Abstracts Collection of Dagstuhl Seminar 08051 "Theory of Evolu-tionary Algorithms", Dagstuhl, 2008, P.2.
Eremeev A. V. On complexity of optimal recombination for binary representations of solutions // Evolutionary Computation, Vol. 16 N 1, 2008, P. 127-147.
Еремеев А. В., Коваленко Ю. В. Приближенное решение одной задачи составления расписаний для многопродуктового производства // Материалы Всероссийской конференции "Проблемы оптимизации и экономические приложения". Омск, 2009. - С. 223.
30. Разработаны методы кластерного анализа, основанные на коллективе (ансамбле) деревьев решений. Исследованы вероятностные свойства ансамбля. Методы применены в задаче сегментации спутниковых изображений.
Разработаны методы кластерного анализа, основанные на коллективе (ансамбле) деревьев решений. Предложена модель ансамблевой классификации, основанная на сведении к задаче распознавания
образов с латентными метками классов. В рамках модели исследовано поведение вероятности ошибки при увеличении числа элементов ансамбля, найдены необходимые условия, при которых ожидаемая ошибка стремится к минимально возможному значению. Предложен новый информационный критерий качества группировки, основанный на байесовской модели распознавания образов по конечному множеству событий. При построении ансамбля учитываются расстояния между логическими высказываниями, описывающими кластеры; кроме того, используется адаптивная процедура выбора случайного подпространства переменных, в котором строится элемент ансамбля. Использование деревьев решений позволяет получать легко интерпретируемые логические модели объектов, дает возможность группировать объекты, описываемые как числовыми, так и нечисловыми переменными, выделять наиболее информативные переменные. Применение ансамбля значительно повышает устойчивость решений по отношению к выбору параметров алгоритма построения дерева. На основе разработанных методов предложен сеточный алгоритм сегментации спутниковых изображений, позволяющий выделять многомодовые кластеры сложной формы. Результаты проведенных экспериментов на модельных и реальных данных подтверждают устойчивость формируемых решений к изменению шага сетки.
Бериков В. Б., Лбов Г. С. Выбор оптимальной сложности класса логических решающих функций в задачах распознавания образов // Доклады Академии наук. 2007. Том 417, N 1. C. 26-29.
Лбов Г. С., Неделько В. М., Неделько С. В. Метод адаптивного поиска логической решающей функции. // Сибирский журнал индустриальной математики, 2009, т. ХII, № 3 (39). С. 66–74.
Бериков В. Б. Кластерный анализ с использованием коллектива деревьев решений // Научный вестник НГТУ. 2009. № 3 (36). С.67-76.
Berikov V. B. Construction of the ensemble of logical models in cluster analysis // D.-S. Huang et al. (Eds.) Emerging Intelligent Computing Technology and Applications. With aspects of artificial intelligence. ICIC 2009. Lecture Notes in Artificial Intelligence, LNAI 5755. Springer-Verlag: Berlin, Heidelberg. 2009. P. 581–590.
Бериков В. Б. Построение ансамбля логических моделей в кластерном анализе // Математические методы распознавания образов: 14-я Всероссийская конференция. Владимирская обл., г. Суздаль. 21–26 сентября 2009 г.: Сборник докладов. – М.: Макс-Пресс, 2009. – С. 85-88.
Пестунов И. А., Куликова Е. А., Бериков В. Б., Махатков И. Д. Сеточный алгоритм кластеризации с использованием ансамблевого подхода к принятию решений // Горный информационно-аналитический бюллетень. – 2009. - № 12. (принята в печать)
31. Показана несостоятельность скрытой локальной симметрии при описании процесса множественного рождения пи-мезонов в электрон-позитронных столкновениях при низких энергиях.
Показано, что киральная модель, включающая псевдоскалярые, векторные и аксиально-векторные мезоны на основе скрытой локальной симметрии, не может описать экспериментальные данные по рождению четырёх заряженных пи-мезонов в электрон-позитронных столкновениях при полной энергии ниже 1 ГэВ и требует введения аномально большого вклада радиальных возбуждений ρ-мезона.
Н. Н. Ачасов и А. А. Кожевников. Письма в ЖЭТФ 88, 3 (2008).
N. N. Achasov and A. A. Kozhevnikov. European Physical Journal A 38, 61 (2008).
|



