| |
Важнейшие научные результаты Института математики за 2008 год
1. Доказана теорема о сохранении гензелевой рациональности нормированных полей при циклических p-расширениях.
Как следствие, получено выполнение AKE-принципа для гензелева ручного поля.
Доказана теорема о сохранении гензелевой рациональности нормированных полей при циклических p-расширениях, что позволило завершить доказательство того, что гензелево ручное поле удовлетворяет AKE-принципу.
Ю. Л. Ершов. О гензелевых рациональных расширениях // ДАН, 422, N4, 2008, 450-454.
2. Получен отрицательный ответ на вопрос Ф. Стефана о совпадении условий
существования алгоритмов индуктивного синтеза программ для порождения семейства множеств конечных текстов
по конечным выборкам и предельной эквивалентности любых вычислимых представлений этих семейств.
В теории индуктивного синтеза методами теории вычислимых нумераций получен отрицательный ответ на вопрос
Ф. Стефана о Txt-распознаваемых (Txt-learnable) семейств языков с предельной эквивалентностью их вычислимых
нумераций, а также показано, что в ослабленном варианте распознаваемости языков BC-распознаваемости
(behaviorly-correct learnable) существуют BC-распознаваемые семейства, которые имеют не предельно
эквивалентные вычислимые нумерации и семейства языков, которые имеют только предельно эквивалентные
нумерации, но не являются BC-распознаваемыми семействами.
Goncharov S. S., Badaev S. A. Computability and Numberings // New Computational Paradigms, Changing Conceptions of what is Computable, ed.: S. B. Cooper, B. Lowe, A. Sorbi, Springer Science + Business Media, LLC, New York, 2008, 19-34.
Klaus Ambos-Spies, Serikzhan Badaev, Goncharov S. S. Inductive Inference and Computable Numberings // In Mathematical Structures in Computer Science, 28 с.
Klaus Ambos-Spies, Serikzhan Badaev, Goncharov S. S. On a Question of Frank Stephan // In Theory and Applications of Models of Computation, Lecture Notes in Comput. Sci., 4978, Springer, Berlin, 2008, 423-432.
3. Получена полная характеризация типов изоморфизма главных идеалов полурешётки арифметических m-степеней.
Получена характеризация типов изоморфизма главных идеалов полурешётки m-степеней, порождённых множествами, входящими в арифметическую иерархию. Доказано, что для произвольных натурального числа n и верхней полурешётки L следующие условия эквивалентны:
1. L является ограниченной дистрибутивной верхней полурешёткой, имеющей Σ0n+3-представление;
2. L изоморфна главному идеалу полурешётки m-степеней, порождённому коиммунным или вычислимым Σ0n+1-множеством;
3. L изоморфна главному идеалу полурешётки m-степеней, порождённому иммунным или вычислимым Π0n+1-множеством;
4. L изоморфна главному идеалу полурешётки m-степеней, порождённому Δ0n+2-множеством.
На основании этого описания дан ответ на некоторые вопросы, относящиеся к теории нумераций. В частности,
доказано, что для произвольного натурального числа n существует ровно 3 типа локального изоморфизма
полурешёток Роджерса R0n+2(F) для конечных семейств F; дано описание этих типов.
Доказано также, что для произвольных n, m≥n+2, F и S нетривиальные полурешётки Роджерса R0n+1(F)
и R0m+1(S) локально не изоморфны. Как следствие, они не могут быть изоморфны, что усиливает полученные
ранее результаты Гончарова, Бадаева и Сорби в этом направлении.
Сибирский Математический Журнал, 2008 г., т. 49, № 6.
4. На основе общей категорной конструкции введено общее понятие многообразия
диалгебр, ассоциированного с произвольным многообразием (обычных или конформных) алгебр. Показано, что
диалгебра Ли в смысле этого определения есть не что иное, как алгебра Лейбница, и доказано, что любая
конечномерная алгебра Лейбница вкладывается в конечномерную ассоциативную диалгебру (аналог теоремы Адо).
Понятие (ассоциативной) диалгебры было введено Ж. Л. Лодеем (1993) для исследования алгебр Лейбница – некоммутативных
аналогов алгебр Ли, возникающих при исследовании когомологий лиевых алгебр. Формально диалгебра представляет собой
пространство с двумя билинейными операциями умножения. Категория ассоциативных диалгебр играет в теории алгебр Лейбница ту же роль,
что категория ассоциативных алгебр – для алгебр Ли. С другой стороны, конформные алгебры были введены В. Г. Кацем (1996)
как формальный язык описания свойств алгебраических структур, возникающих в математической физике, а именно, вертексных алгебр. Нами обнаружена связь между этими двумя понятиями: построен функтор C→C(0) из категории
конформных алгебр в категорию диалгебр, сохраняющий принадлежность объекта любому из известных в литературе
многообразий диалгебр (ассоциативные, коммутативные, альтернативные). Операции диалгебры на C(0) оказываются
заданными через операторы левого и правого 0-умножения на конформной алгебре C. При помощи общего подхода,
использующего понятие операды (Дж. Мэй, 1972) введено понятие многообразия Var-диалгебры, ассоциированного
с данным семейством обычных однородных полилинейных тождеств, определяющих многообразие Var обычных
(или конформных) алгебр. Это определение согласовано с известными ранее понятиями ассоциативной,
коммутативной и альтернативной диалгебр. Доказана
Теорема 1. Если C – конформная алгебра многообразия Var, то C(0) – Var-диалгебра.
Показано, что функтор C→C(0) обратим в следующем смысле.
Теорема 2. Если D – диалгебра многообразия Var, то найдется конформная алгебра C многообразия Var такая, что D C(0). C(0).
В частности, класс диалгебр Ли совпадает с классом алгебр Лейбница. Используя построенное вложение любой диалгебры Ли в конформную алгебру Ли, доказана
Теорема 3. Любая (конечномерная) алгебра Лейбница имеет точное конформное представление конечного типа.
Следствие (аналог теоремы Адо). Любая конечномерная алгебра Лейбница вкладывается в конечномерную ассоциативную диалгебру.
Колесников П. С. Многообразия диалгебр и конформные алгебры // Сиб. мат. журн. 2008. Т. 49, №2. С. 323-340.
Колесников П. С. Конформные представления алгебр Лейбница // Сиб. мат. журн. 2008. Т. 49, №3. С. 540-547.
5. Для каждой конечной простой линейной группы над полем четного порядка описаны
все изоспектральные ей конечные группы. В частности, доказано, что любая такая линейная группа почти
распознаваема, а также установлено, при каких условиях она является распознаваемой.
Спектром группы называется множество порядков ее элементов. Две группы называются изоспектральными, если их спектры равны. Конечная группа называется распознаваемой по спектру, если она изоморфна любой изоспектральной ей конечной группе, и почти распознаваемой по спектру, если существует только конечное число попарно неизоморфных изоспектральных ей конечных групп.
Пусть L - конечная простая линейная группа над полем четного порядка. Доказано, что необходимым условием того, что конечная группа изоспектральна L, является ее изоморфность расширению группы L с помощью некоторого полевого автоморфизма. Как следствие, установлено, что группа L почти распознаваема по спектру. Найдены достаточные условия изоспектральности группы L и ее автоморфного расширения.
В частности, получен критерий распознаваемости группы L по спектру.
Алгебра и логика, т. 47 (2008), № 1, с. 83-93, № 4, с. 405-427, и № 5, с. 558-570.
6. Установлена распознаваемость среди накрытий простых линейных групп проективной
размерности, отличной от четырёх, и найден пример нераспознаваемой среди накрытий группы размерности четыре.
Напомним, что спектром ω(H) конечной группы H называется множество порядков её элементов. Говорят, что H
распознаваема (по спектру) среди своих накрытий, если для любой конечной группы G, накрывающей H
(т. е. для которой H является гомоморфным образом), равенство спектров ω(G)=ω(H) влечёт изоморфизм.
Исследование распознаваемости среди накрытий является важной подзадачей более общей проблемы распознаваемости
конечных групп по спектру и сводится к рассмотрению неприводимых модулярных представлений. В "Коуровскую тетрадь"
В. Д. Мазуров внёс вопрос (проблема 14.60), являются ли распознаваемыми среди накрытий простые группы PSLn(q)
при n≥3.
Доказано, что если конечная простая группа, изоморфная PSLn(q) или PSUn(q) действует на конечномерном векторном
пространстве над полем, характеристика которого совпадает с характеристикой определения группы, то соответствующее
полупрямое произведение содержит элемент, порядок которого отличен от всех порядков элементов исходной простой
группы, если выполнено одно из условий: n отлично от 4, q простое, q чётное. Отсюда в качестве следствия вытекает
распознаваемость среди накрытий проективных линейных групп PSLn(q) при n≥4. Среди групп PSL4(q) найден пример группы,
не распознаваемой по спектру среди накрытий. Отсюда вытекает решение проблемы 14.60 из "Коуровской тетради".
Заварницин А. В. Свойства порядков элементов в накрытиях групп Ln(q) и Un(q) // Сиб. Матем. Журн. 2008. Т. 49, № 2. С. 309-322.
Заварницин А. В. О распознаваемости по спектру среди накрытий конечных простых линейных и унитарных групп // Доклады Академии Наук 2008. Т. 421, № 1. С. 11-14.
Zavarnitsine A. V. Exceptional action of the simple groups L4(q) in the defining characteristic // Siberian Electronic Math. Reports. 2008. V. 5. P. 68-74
7. Доказана теорема единственности решения задачи интегральной геометрии, заключающейся в нахождении
поверхностей разрывов подынтегральной функции через известные интегралы по всевозможным прямым в n-мерном пространстве (n>1).
Рассматривается задача, в которой заданы интегралы по всем прямым от неизвестной кусочно-гладкой функции f(x,ω,y), xєG, ωєΩ, yєG, где G – заданная ограниченная область в Rn, n>1, Ω – единичная сфера в Rn. Интегрирование по прямым {x+tω, tєR1} производится по переменной y, т.е. заданы интегралы:
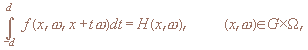
где d – диаметр области G, а функция f(x,ω,y) продолжена по y нулем вне G. Подынтегральная функция, которая считается неизвестной, зависит от 3n-1 независимых переменных, а известная функция H(x,ω) зависит только от 2n-1 переменных. Поэтому единственность решения задачи об определении подынтегральной функции вряд ли имеет место. Вместе с тем, именно подобные проблемы нередко возникают при исследовании обратных задач для уравнений математической физики, если использовать достаточно полные математические модели. В частности, к таким вопросам сводятся задачи рентгеновской томографии произвольных сред и для произвольных зондирующих излучений.
Ввиду того, что определить полностью подынтегральную функцию не представляется возможным, ставится более скромная задача нахождения ее поверхностей разрывов по переменной y. Важно отметить, что в ряде случаев, знание указанных поверхностей дает неплохое представление о неизвестном объекте. Например, для проблем локации или дефектоскопии умение найти границы внутренних неоднородностей представляется вполне достаточным.
Доказана теорема единственности решения поставленной задачи интегральной геометрии при ограничениях только общего характера и при условии наличия ненулевых разрывов по y подынтегральной функции на искомых поверхностях. Доказательство имеет отчетливый конструктивный характер, дающий простой способ построения соответствующего алгоритма.
Использованный метод позволяют надеяться на возможность дальнейшего обобщения результатов, например, для случая, когда интегрирование производится по семейству кривых, причем, не только подынтегральная функция, но и кривые могут считаться неизвестными.
Исследование выполнено в рамках нового подхода к обратным задачам, который состоит в выделении сравнительно простых частей из сложного выражения, соответствующего исходным данным. Эта проблема может рассматриваться, как мало изученная задача функциональных уравнений.
Аниконов Д. С. Специальная задача интегральной геометрии // Доклады АН, 2007, Т. 415, №1, С.7-9.
Аниконов Д. С. Индикатор контактных границ для задачи интегральной
геометрии // Сибирский математический журнал, 2008, Т. 49, № 4, С.739-755.
8. Доказано, что геометрия пространства Карно – Каратеодори моделируется локально геометрией нильпотентной градуированной группы Ли, определяемой структурными постоянными исходного многообразия.
Этот результат применяется для вывода формулы площади.
Доказательство результатов о сравнении локальных геометрий локальных групп Карно на пространстве Карно - Каратеодори
опирается на известную теорему Громова о сходимости масштабированных векторных полей к полям, которые
являются базисом некоторой нильпотентной градуированной алгебры Ли. Получено новое доказательство этой
теоремы (взамен ошибочного у Громова), которое работает и при минимальной гладкости векторных полей.
Из этого результата выводятся факты, лежащие в основаниях субримановой геометрии. Эти результаты применяются
при доказательстве субриманова аналога теоремы Радемахера о дифференцируемости почти всюду липшицевых
отображений. В качестве приложения получена субриманова формула площади для липшицевых (в субримановом
смысле) отображений. Метод доказательства является новым и для липшицевых в классическом смысле отображений
евклидовых пространств.
Водопьянов С. К., Карманова М. Б. Субриманова геометрия при минимальной гладкости векторных полей. ДАН. 2008. Т. 422, No 5. С. 583-588.
Водопьянов С. К., Карманова М. Б. Формула площади для C1-гладких контактных отображений многообразий Карно. ДАН 2008. Т. 422, No 1. С. 15-20.
Карманова М. Б. Формула площади для липшицевых отображений пространств Карно-Каратеодори. ДАН 2008. Том 423, No 5. С. 602-606.
9. Получены достаточные условия абсолютной непрерывности функций соболевского типа,
удовлетворяющих неравенству Пуанкаре на s-регулярных метрических пространствах.
В достаточно общей ситуации, включающей в себя евклидов случай, получено обобщение относительно недавнего
результата об абсолютной непрерывности функций, имеющих обобщенные производные в областях евклидова
пространства (Kauhanen J., Koskela P., Maly J., 1999). На полном метрическом пространстве (X,d)
с s-регулярной мерой изучаются свойства функций, удовлетворяющих метрическому аналогу p-неравенства Пуанкаре.
При 1<p<s< для функций, удовлетворяющих p-неравенства Пуанкаре на s-регулярном метрическом пространстве (X,d),
доказана s-абсолютная непрерывность в случае, когда "метрический аналог градиента" принадлежит соответствующему
пространству Лоренца Ls,1. Для метрического случая разработаны новые методы доказательства, которые
существенно отличаются от доказательств для евклидова случая. При этом соответствующий результат для
евклидова случая может быть получен как следствие общего результата для s-регулярных метрических пространств.
Романов А. С. О непрерывности функций соболевского типа на метрических пространствах // Доклады РАН. 2008. Т. 418, № 5. С. 599-602.
Романов А. С. Об абсолютной непрерывности функций соболевского типа на метрических пространствах // Сиб. мат. журн. 2008. Т. 49, № 5. C. 1148-1157.
10. Доказана устойчивость некоторых классов решений нелинейных дифференциальных
уравнений в частных производных первого порядка, построенных с помощью квазивыпуклых функций и нуль-лагранжианов.
Для этих классов решений установлены оценки устойчивости в равномерной норме на компактно вложенных
подобластях. В предположении строгой квазивыпуклости в добавлении к оценкам в равномерной норме получены
оценки близости в соболевской норме.
Егоров А. А. Квазивыпуклые функции и нуль-лагранжианы в проблемах устойчивости классов отображений. Сиб. мат. журн. 2008. Т. 49, N 4. С. 796-812.
11. Доказана теорема Михлина об ограниченности в Lp, 1<p<∞, одного класса сингулярных интегральных операторов, действующих на функции, заданные в областях групп Карно.
Подобные операторы, действующие на функции, заданные в областях евклидова пространства, были рассмотрены
С. Г. Михлиным. Теорема Михлина представляет собой широко применяемое в смежных областях обобщение теоремы
Зигмунда-Кальдерона об ограниченности сингулярного интегрального оператора. Полученное обобщение этого
результата на группы Карно тесно связано с теорией субэллиптических уравнений.
Романовский Н. Н. О проблеме Михлина на группах Карно. Сиб. Мат. Журн. 2008. Т. 49, No 1. С. 193-206.
12. С помощью преобразования Мутара построены двумерные операторы Шредингера с
быстро убывающими гладкими потенциалами и нетривиальными L2-ядрами и распадающиеся за конечное время решения
уравнения Веселова-Новикова с быстро убывающими гладкими начальными данными Коши.
Преобразование Мутара является обобщением преобразования Дарбу на случай двумерных операторов Шредингера.
Преобразование Дарбу широко использовалась в спектральной теории для построения интересных примеров
операторов с различными замечательными свойствами. Оно, в частности, позволяет строить по интегрируемым
одномерным потенциалам новые интегрируемые потенциалы.
Преобразование Мутара до настоящего времени в спектральной теории не использовалось. С его помощью нам
удалось построить гладкие потенциалы оператора Шредингера на двумерной плоскости, убывающие как r−8,
с кратным L2-ядром. Заметим, что в одномерном случае для быстро убывающих потенциалов ядро оператора
Шредингера нулевое. До настоящей работы примеров двумерных операторов Шредингера с быстро убывающим
потенциалом и нетривиальным ядром известно не было.
Уравнение Веселова-Новикова является интегрируемой двумеризацией уравнения Кортевега-де Фриза,
для которого решения с быстро убывающими регулярными данными Коши являются регулярными. С помощью
преобразования Мутара нами построены явные распадающиеся (blowing up) решения уравнения Веселова-Новикова
с регулярными данными задачи Коши, убывающими как r−3.
И. А. Тайманов, С. П. Царев. Распадающиеся решения уравнения Веселова-Новикова. ДАН. 2008. Т. 420, N. 6. С. 744-745.
И. А. Тайманов, С. П. Царев. Двумерные рациональные солитоны, построенные с помощью преобразования Мутара, и их распад. Теор. и матем. физика. 2008. Т. 157, N 2. С. 188-207.
13. Разработана новая параметризация неизвестных в уравнениях нелинейной теории
упругости, обеспечивающая корректность (локальную на гладких решениях) задачи Коши.
На основе этой неожиданной параметризации и на использовании стандартного метода Годунова, с линеаризованными
задачами Римана, построена вычислительно реализуемая дискретная модель, позволившая моделировать не только
гладкие, но и разрывные решения, описывающие деформации, вызванные взрывными нагрузками. Модификация модели,
путём введения в неё максвелловских релаксаций, применима для моделирования пластических (необратимых)
деформаций.
С. К. Годунов, И. М. Пешков. Симметрические гиперболические уравнения нелинейной теории упругости. ЖВМиМФ, 2008. Т. 48, № 6. С. 1034-1055.
14. Получено новое дифференциальное тождество, связанное с оператором квантового кинетического уравнения. На основе этого тождества доказана теорема единственности решения линейной обратной задачи.
Квантовое кинетическое уравнение имеет вид
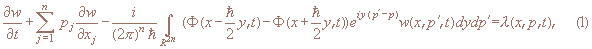
где  — область с гладкой границей
∂D вещественного евклидова пространства Rn, t≥0, Φ(x,t) – потенциал, w(x,p,t) – квантовая функция распределения – функция Вигнера, λ(x,p,t) – функция источников, возможно функционально-интегрально зависящая от w при наличии столкновительных явлений,
ħ – постоянная Планка. — область с гладкой границей
∂D вещественного евклидова пространства Rn, t≥0, Φ(x,t) – потенциал, w(x,p,t) – квантовая функция распределения – функция Вигнера, λ(x,p,t) – функция источников, возможно функционально-интегрально зависящая от w при наличии столкновительных явлений,
ħ – постоянная Планка.
Предполагая наличие всех производных функций w(x,p,t), Φ(x,t) разложением подынтегрального выражения уравнения (1) в ряд Тейлора по
ħ получают квантовое кинетическое уравнение бесконечного порядка
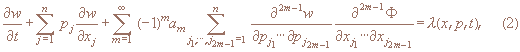
где
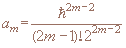
Конечные приближения уравнения, в том случае и классические (N=1), следуют из (2) стандартным способом – отбрасыванием бесконечного числа слагаемых:
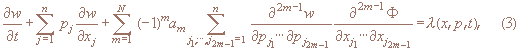
Cправедливо следующее утверждение. Пусть функции w(x,p,t), Φ(x,t) дифференцируемы достаточное число раз. Тогда имеет место тождество:
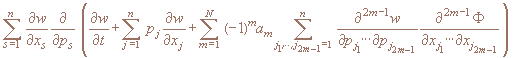
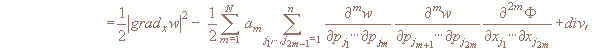
где
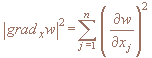
и под div понимаются дивергентные слагаемые по переменным x, p, t.
Обратная задача определения правой части.
Рассмотрим обратную задачу поиска бесконечно дифференцируемых функций w(x,p,t), λ(x,p,t),
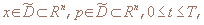 таких, что таких, что
1)
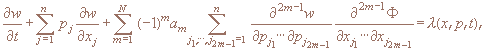
2) 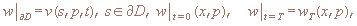
3) 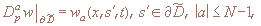 где где
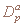 – дифференцирование по переменным p, α – мультииндекс. – дифференцирование по переменным p, α – мультииндекс.
Теорема. Если
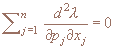 и квадратичные формы и квадратичные формы
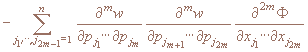
положительно определены, m=1,...,N, то обратная задача 1)-3) поиска функций в области
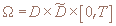 имеет
не более одного бесконечно дифференцируемого решения (w(x,p,t),λ(x,p,t)) в замыкании
имеет
не более одного бесконечно дифференцируемого решения (w(x,p,t),λ(x,p,t)) в замыкании
 . .
Аниконов Ю. Е., Нещадим М. В., Тождество для приближенных квантовых уравнений и обратные задачи, Сибирский журнал индустриальной математики, т. 10, N 4, 2007, с. 3-9.
Аниконов Ю. Е., Нещадим М. В., Некоторые обратные задачи для квантового кинетического уравнения, Вестник Новосибирского государственного университета, т. 8, N 4, 2008.
15. Для уравнений магнитной гидродинамики доказано существование лаксовских ударных волн,
вязкие профили которых нелинейно устойчивы относительно одномерных возмущений, а соответствующие сильные
разрывы неустойчивы относительно многомерных возмущений.
На примере уравнений магнитной гидродинамики доказано существование лаксовских ударных волн, вязкие профили которых нелинейно устойчивы относительно одномерных возмущений, а соответствующие сильные разрывы неустойчивы относительно многомерных возмущений. Важно отметить, что в газовой динамике ударные волны с таким свойством отсутствуют. Полученный результат указывает на то, что учет диссипативных процессов при исследовании ударных волн хотя и является очень важным моментом с физической точки зрения, но, будучи проведенным на одномерном уровне, явно недостаточен для обоснования физической реализуемости течения с ударной волной. Доказательство существования лаксовских ударных волн с вышеописанным свойством проведено аналитически и опирается на применение энергетического метода для возмущений нулевой массы для вязких законов сохранения, а также на асимптотическое разложение по малому параметру определителя Лопатинского-Крайса.
Freistuhler H., Trakhinin Y. On viscous and inviscid stability of magnetohydrodynamic shock waves. Physica D 237 (2008), 3030-3037.
16. Установлена нётеровость краевых задач в Rn+ для квазиэллиптических систем, получены необходимые и достаточные условия разрешимости в соболевских пространствах. Доказаны теоремы об изоморфизме для классов матричных квазиэллиптических операторов в Rn в специальных шкалах весовых соболевских пространств.
Цикл работ посвящен изучению свойств матричных квазиэллиптических операторов во всем пространстве Rn и
полупространстве Rn+, а также исследованию задач для систем соболевского типа. Для операторов в Rn доказаны
теоремы об изоморфизме в специальных шкалах соболевских пространств со степенными весами. Эти теоремы
применяются для доказательства безусловной разрешимости начальных задач для классов систем уравнений соболевского типа, а также для изучения асимптотических свойств решений на
бесконечности. Для краевых задач в Rn+ для квазиэллиптических систем исследованы вопросы разрешимости в
различных шкалах соболевских пространств. Доказаны теоремы о нетеровости краевых задач, удовлетворяющих
условию Лопатинского, получены оценки индексов краевых задач. Установлены достаточные условия разрешимости в
соболевских пространствах Wlp, выделен класс краевых задач, для которых эти условия являются необходимыми.
Выделены классы безусловно разрешимых краевых задач. Из доказанных теорем вытекает, что индекс краевых задач
в Rn+ в соболевских пространствах зависит от порядков операторов, размерности пространства n, степени
суммируемости p, а также от выполнения некоторых новых интегральных условий на символы дифференциальных
операторов.
Demidenko G. V. Mapping properties of quasielliptic operators and applications // Int. J. Dynamical Systems and Differential Equations. 2007. V. 1, No 1. P.58-67.
Бондарь Л. Н. Условия разрешимости краевых задач для квазиэллиптических систем // Вестн. НГУ. Сер.: Математика, механика, информатика. 2007. Т. 7, вып. 4. С. 9-26.
Бондарь Л. Н. Поведение решения на бесконечности одной системы соболевского типа // Сиб. мат. журн. 2007. Т. 48, No 5. С. 980-994.
Бондарь Л. Н., Демиденко Г. В. Краевые задачи для квазиэллиптических систем // Сиб. мат. журн. 2008. Т. 49, No 2. С. 256-273.
Демиденко Г. В. Квазиэллиптические операторы и уравнения соболевского типа // Сиб. мат. журн. 2008. Т. 49, No 5. С. 1064-1076.
17. Завершен цикл работ, посвященных изучению вероятностей больших уклонений сумм
независимых одинаково распределенных случайных векторов. Получены интегро-локальные теоремы для уклонений на
границе и вне крамеровской области, а также для сверхбольших уклонений.
В течение последних 50-60 лет шло интенсивное изучение асимптотического поведения распределений сумм случайных векторов, связанное со многими прикладными задачами. Однако исследования проводились лишь для уклонений, сосредоточенных в так называемой крамеровской области (области аналитичности функции уклонений). Вне этой области возникает качественно иная асимптотика, требующая для своего изучения новых подходов. Такие подходы за последние годы авторами были разработаны. В результате удалось получить исчерпывающее в известном смысле описание требуемой асимптотики в весьма точной форме (в терминах интегро-локальных теорем) для уклонений во всем пространстве, включая сверхбольшие уклонения.
Borovkov A. A., Borovkov K. A. Asymptotic analysis of random walks. Heavy tailed distributions. Cambridge University Press. 2008, 623 p.
Боровков А. А., Могульский А. А. О больших и сверхбольших уклонениях сумм независимых случайных векторов при выполнении условия Крамера. I. Теория вероятностей и ее применения, 2006, Т.51, N2, С.260-294.
Боровков А. А., Могульский А. А. О больших и сверхбольших уклонениях сумм независимых случайных векторов при выполнении условия Крамера. II. Теория вероятностей и ее применения, 2006, Т.51, N4, С.641-673.
Боровков А. А., Могульский А. А. Предельные теоремы для сумм случайных величин с семиэкспоненциальными распределениями, действующие на всей оси. Сибирский Математический журнал, 2006, Т. 47, N 6, 1218-1257.
Могульский А. А., Пагма Ч. Сверхбольшие уклонения сумм случайных величин с общим арифметическим суперэкспоненциальным распределением. Математические труды. 2008, Т. 11, N1, С.81-112.
Могульский А. А. Интегро-локальная теорема, действующая на всей полуоси, для сумм случайных величин с правильно меняющимися распределениями. Сибирский математический журнал. 2008, Т. 49, N4, С.837-854.
Боровков А. А., Могульский А. А. Вероятности больших уклонений для сумм независимых случайных векторов на границе и вне крамеровской зоны.I. Теория вероятн. и ее примен. 2008, Т. 53, N2, С.336-344.
Боровков А. А., Могульский А. А. Вероятности больших уклонений для сумм независимых случайных векторов на границе и вне крамеровской зоны.II. Теория вероятн. и ее примен. 2008, Т. 53, N4.
18. Получены предельные теоремы для распределений симметрических нелинейных
статистик (так называемых канонических U- и V-статистик), построенных по выборкам растущего объема слабо
зависимых наблюдений.
Исследование нелинейных функционалов от эмпирических распределений – так называемых функционалов Мизеса
(или V-статистик) и родственных объектов – U-статистик, берет своё начало с основополагающих работ Р. Мизеса
(1947) и В. Хёфдинга (1948). К началу нового века в основном была сформирована предельная теория (включая
вероятностные неравенства) для этого важного класса статистик в случае независимых наблюдений. С конца 70-х
годов началось также изучение этих статистик в случае зависимых стационарно связанных наблюдений.
В представленных работах авторами описаны предельные распределения так называемых канонических U- и V-статистик
в случае зависимых наблюдений растущего объема с сильным или равномерно сильным перемешиванием.
При этом случайная величина, соответствующая предельному распределению, допускает представление в виде
кратного ряда, построенного по последовательности зависимых гауссовских центрированных случайных величин с
известной ковариацией. Ранее удавалось получать подобные результаты только для более сильного типа зависимости –
так называемого "пси"-перемешивания. Кроме того, получены экспоненциальные неравенства (аналоги неравенства
Хёфдинга) для распределений U- и V-статистик от последовательности зависимых случайных величин с равномерно
сильным перемешиванием.
Борисов И. С., Володько Н. В. Ортогональные ряды и предельные теоремы для канонических U- и V-статистик от стационарно связанных наблюдений. Математические Труды, 2008, 11(1), с. 25-48.
Борисов И. С., Володько Н. В. Экспоненциальные неравенства для распределений канонических U- и V-статистик от зависимых наблюдений. Математические Труды, 2008, 11(2), с. 3-19.
19. Получены достаточные условия формосохранения (положительности, монотонности, выпуклости и т.д.) интерполяционного кубического сплайна.
Под формосохраняющей интерполяцией понимается интерполяция с наследованием интерполянтом положительности
исходной функции или одной из её производных. Наиболее востребованными и используемыми в подавляющем
большинстве задач, связанных с практическим приближением функций, являются кубические сплайны класса C2.
Однако при интерполяции такие сплайны, вообще говоря, не сохраняют такие геометрические свойства интерполируемой
функции, как знакопостоянство производных и самой функции. Вместе с тем имеется большое количество задач,
где от аппроксимирующей функции требуется именно сохранение таких геометрических характеристик, поэтому для
гарантированного достижения целей приходится привлекать другой аппарат, как правило, уступающий оптимальным
кубическим сплайнам по аппроксимативным свойствам, сложности реализации или по другим качествам. Поэтому
представляется естественным в тех задачах, где можно гарантировать выполнение требуемых свойств классическим
кубическим сплайном, использовать именно кубические сплайны. Авторами установлены достаточные легко проверяемые
априорно условия положительности любой производной интерполяционного кубического сплайна.
Богданов В. В., Волков Ю. С. Выбор параметров обобщённых кубических сплайнов при выпуклой интерполяции // Сибирский журнал вычислительной математики. 2006. Т. 9, № 1. С.5-22.
Волков Ю. С. О нахождении полного интерполяционного сплайна через B-сплайны // Сибирские электронные математические известия. 2008. Т. 5. С. 334-338.
Волков Ю. С., Богданов В. В., Мирошниченко В. Л., Шевалдин В. Т. Формосохраняющая интерполяция кубическими сплайнами. Математические заметки, 11 с. (в печати)
Волков Ю. С., Богданов В. В. Формосохраняющая интерполяция кубическими сплайнами. Международная конференция, посвящённая 100-летию С. Л. Соболева. Новосибирск: ИМ СО РАН, 2008. С. 464.
20. Предложен способ сплайн-интерполяции функций одной переменной с большими градиентами, основанный на выделении аддитивной составляющей, задающей основной рост. Показано, что формулы линейной и квадратической сплайн-интерполяции обладают равномерной точностью на априорно сгущающихся сетках.
Известно, что при применении методов полиномиальной сплайн-интерполяции к функциям с большими градиентами могут возникать существенные погрешности. Однако, если известен вид составляющей, отвечающей за рост решения, то это можно учесть при построении сплайн-интерполяционной формулы. В случае произвольной сетки построена сплайн-интерполяционная формула, точная на погранслойной составляющей, первого порядка точности независимо от градиентов интерполируемой функции. Показано, что построенная формула может быть применена в случаях, когда интерполируемая функция является решением задачи с экспоненциальным или степенным пограничным слоем, распространена на случай функции двух переменных. Показано, что при использовании сетки, априорно сгущающейся в пограничном слое, линейная и квадратическая сплайн-интерполяции обладают равномерной точностью второго и третьего порядка, соответственно, по числу узлов. Показано, как на основе предложенной сплайн-интерполяции можно построить двухсеточный алгоритм решения нелинейной сингулярно-возмущенной краевой задачи. Предложенная сплайн-интерполяция в этом алгоритме необходима при интерполяции сеточного решения с крупной сетки на мелкую.
Задорин А. И. Метод интерполяции для задачи с пограничным слоем // Сибирский журнал вычислительной математики, 2007, т. 10, № 3, с. 267- 275.
Задорин А. И. Метод интерполяции для функции двух переменных с погранслойной составляющей // Вычислительные технологии, 2008, т. 13, № 3, с. 45-53.
Задорин А. И. Метод интерполяции на сгущающейся сетке для функции с погранслойной составляющей // Журнал вычислительной математики и математической физики, 2008, т. 48, № 9, с. 1673-1684.
L. G. Vulkov, A. I. Zadorin. Two-grid Interpolation Algorithms for Difference Schemes of Exponential Type for Semilinear Diffusion Convection-Dominated Equations. // American Institute of Physics, Conference proceedings, 2008, v. 1067, p. 284- 292.
21. Построена модель смешанной экономики типа Эрроу-Дебре. На основе гомотопического подхода получены условия существования равновесных цен для этой модели, близкие к самым общим предположениям теорем существования равновесия в классической модели Эрроу-Дебре. Найден широкий класс смешанных экономик типа Эрроу-Дебре с максимально возможной областью нетангенциальности их отображений избыточного спроса.
Представлены результаты исследований смешанной экономической системы типа Эрроу-Дебре – одной из наиболее важных реализаций общей концепции двухуровневой экономики, предложенной акад. В. Л. Макаровым еще в конце 1970-х годов. Стандартная система Эрроу-Дебре, как известно, включает в явном виде производственный сектор, что значительно усугубляет трудности анализа ее смешанного аналога, связанные с нелинейностью индивидуальных функций дохода участников. Тем не менее, для предложенной в работе модели смешанной экономики с элементами централизованного управления удалось получить теорему существования равновесных цен при условиях, близких к самым общим предположениям, гарантирующим существование равновесия в классических моделях Эрроу-Дебре. Доказательство теоремы существования использует гомотопический подход, основанный на рассмотрении однопараметрического семейства смешанных экономик, включающего некоторую предельную, "почти стандартную" систему типа Эрроу-Дебре. Искомый результат достигается применением подходящего геометрического аналога теоремы о неподвижной точке для изучения отображения избыточного спроса в моделях, достаточно близких к указанной предельной системе.
Симбиоз двух механизмов регулирования приводит к тому, что рассматриваемые модели, в отличие от стандартных, не удовлетворяют известному закону Вальраса (т.е. векторные поля, порождаемые их отображениями избыточного спроса, не являются тангенциальными). Поскольку учет нетангенциальности играет ключевую роль при разработке новых методов получения теорем существования, в работе уделяется значительное внимание анализу условий, приводящих к нарушению закона Вальраса. В частности, найден достаточно широкий класс моделей, чьи области нетангенциальности включают все свободные рыночные цены, кроме тех, которые выше цен государственного сектора. Доказано, что такая "максимальная нетангенциальность" устойчива относительно малых возмущений
.
V. Vasil'ev (with H. Wiesmeth). Equilibrium in a mixed economy of Arrow-Debreu type // Journal of Mathematical Economics, 2008, v. 44, pp. 132-147.
22. Впервые построены бесконечные семейства плоских 4-хроматических и реберно
4-критических графов, образованных пересечением замкнутых кривых на плоскости и, тем самым, опровергнута
гипотеза Грёцша-Закса-Кeстера о 3-раскрашиваемости графов этого класса.
Граф Грёцша-Закса образован суперпозицией множества простых замкнутых кривых на плоскости (кривые не имеют
самопересечений, не касаются друг друга, и никакие три кривые не имеют общей точки). Вершины графа
соответствуют точкам пересечения кривых, а ребра - дугам кривых. Вопрос о вершинном хроматическом числе
таких графов восходит к работам Грецша, Закса, Кeстера, Жеже (50-80 гг. XX в.). Известно, что, если граф
порождается пересечением трех кривых, то он является 3-раскрашиваемым (Кестер, Жеже). В середине 80-х годов
Кeстер нашел два 4-хроматических графа, полученных пересечением 5 и 7 кривых. Построено бесконечное семейство
4-хроматических и реберно 4-критических графов, опровергающих гипотезу Грёцша-Закса-Кeстера о 3-раскрашиваемости графов.
Построены бесконечные семейства 4-хроматических графов, полученных пересечением окружностей на плоскости
Dobrynin A. A., Mel'nikov L. S. Two 4-critical Grotzsch-Sachs graphs generated by four curves in the plane // Siberian Elec-tronic Math. Reports, 2008, V. 5, P. 255-278.
Добрынин А. А., Мельников Л. С. Раскраска графов Грецша-Закса // Доклады Одесского семинара по дискретной математике, 2008. N 8. С. 14-24, изд-во Друк: Одесса.
Dobrynin A. A., Mel'nikov L. S. Infinite families of 4-chromatic Grotzsch-Sachs graphs. // J. Graph Theory (в печати).
Dobrynin A. A., Mel'nikov L. S. 4-chromatic edge critical Grotzsch-Sachs graphs // Discrete Math. (в печати).
23. Для k≥3, r>1 получены нижние оценки числа (k,r)-неразделённых семейств подмножеств n-элементного множества ((k,r)-неразделённых булевых функций).
В дискретной математике известна следующая комбинаторная задача. Пусть S n-элементное множество,
а k и r – натуральные числа. Требуется найти асимптотики для числа семейств подмножеств множества S таких,
что в пересечении любых k членов каждого семейства содержится не менее r элементов. А. Д. Коршуновым
найдены нижние оценки для числа таких семейств при любых фиксированных k≥3, r≥1 и n→∞.
Предполагается, что эти оценки совпадают с верхними (пока недоказанными) оценками для числа таких семейств.
Математические вопросы кибернетики. Вып. 16. 2007. С. 31-42.
24. Разработан прямой комбинаторный (свитчинговый) метод построения q-значных совершенных кодов, на его основе исследована проблема пересечений q-значных (q>2) совершенных кодов, получен широкий спектр возможных пересечений совершенных q-значных кодов.
Предложен прямой комбинаторный (свитчинговый) метод построения q-значных совершенных кодов, позволяющий строить широкий класс неэквивалентных совершенных кодов, с дважды экспоненциальной нижней оценкой. Применение этого метода построения позволило исследовать проблему пересечения q-значных совершенных кодов: какие возможны мощности пересечения двух совершенных q-значных кодов длины N? Эта проблема была сформулирована в 1998 г. Т. Этционом и А. Варди, ими же было предложено полное решение проблемы пересечения двоичных кодов Хэмминга (линейных совершенных двоичных кодов), получены возможные пересечения совершенных двоичных кодов с помощью простых свитчингов двоичных кодов Хэмминга. В 2005-2006 гг. С. В. Августинович, У. Хеден и Ф. И. Соловьева существенно продвинулись в решении проблемы пересечения для двоичных нелинейных кодов. Используя прямые комбинаторные (свитчинговые) методы построения q-значных совершенных кодов, получен широкий спектр возможных пересечений q-значных нелинейных совершенных кодов. Следует отметить, что эта проблема тесно взаимосвязана с проблемой классификации всех q-значных совершенных кодов.
Лось А. В. Построение совершенных q-ичных кодов свитчингами простых компонент // Пробл. передачи информ. 2006. Т. 42. № 1. С. 34-42.
Соловьева Ф. И., Лось А. В. О пересечениях q-значных совершенных кодов // СМЖ. 2008. Т. 49. N 2. С. 465-475.
Solov'eva F. I., Los' A. V. On intersections of q-ary perfect codes, Proc. Tenth Int. Workshop "Algebraic and Combinatorial Coding Theory", Zvenigorod, Russia, 248-251 (2006).
25. Построены бесконечные серии диаметрально совершенных кодов с расстоянием 3 и
5 в пространстве троичных слов длины n и веса n-1 с метрикой Хэмминга. Доказано, что коды с расстоянием 3
неэквивалентны полученным ранее (1999 г.), а серия диаметрально совершенных кодов с расстоянием 5 получена впервые.
Множество в дискретном метрическом пространстве называется кодом с расстоянием d, если d есть минимальное
расстояние между двумя различными вершинами кода. Код с расстоянием d называется диаметрально совершенным,
если любое максимальное по мощности множество диаметра меньше d содержит ровно одну кодовую вершину.
Диаметрально совершенные коды являются оптимальными, поскольку не существует кода большей мощности с тем же
кодовым расстоянием (при естественном условии, что пространство достаточно симметричное, то есть его группа
изометрий транзитивно действует на его вершинах). Мы рассматриваем пространство слов длины n в алфавите {0,1,*},
содержащих ровно одну звездочку, с метрикой Хэмминга (расстояние между словами есть число позиций в которых
они различны; данное пространство эквивалентно пространству троичных слов длины n веса n-1). Каждое такое
слово можно трактовать как пару двоичных слов, различающихся ровно в одной позиции, то есть как ребро
n-мерного гиперкуба. В рассматриваемом пространстве максимальные множества диаметра 2, 3 и 4 имеют мощность n,
3n-2 и n2 соответственно. Поскольку мощность всего пространства n2n-1, диаметрально совершенные коды с
расстояниями 3, 4 и 5 должны иметь мощности 2n/n, 2n/(3n-2) и 2n/n2 соответственно. Диаметрально совершенные
коды с расстоянием 4 в рассматриваемом пространстве существуют только при n=6.
Коды с расстоянием 3 были построены в 1999 году шведским математиком М. Сванстрёмом; они соответствуют
совершенному паросочетанию в гиперкубе без близких (на расстоянии 1 или 2) параллельных ребер.
Мы строим неэквивалентные коды с теми же параметрами и впервые строим класс диаметрально совершенных кодов
с расстоянием 5. Для построения последних используются биективные APN (almost perfect nonlinear –
почти совершенно нелинейные) функции {0,1}m→{0,1}m. Такие функции известны для любого нечетного m,
что дает нам коды длины 2m= 8, 32, 128, ..., где m нечетно. Существование диаметрально совершенных кодов с
расстоянием 5 длин 16, 64, 128 ... остается вод вопросом и связано с одной из известнейших открытых проблем
теории нелинейных функций – существованию APN перестановки при четном m.
D. S. Krotov. On diameter perfect constant-weight ternary codes // Discrete Mathematics 308(14) 2008, 3104–3114.
26. Доказана NP-полнота задачи о существовании во множестве векторов евклидова
пространства такого подмножества векторов неизвестной мощности, что среднее значение квадрата длины их суммы
не меньше заданного положительного числа. Для оптимизационного варианта этой задачи обоснован приближённый
асимптотически точный алгоритм, полиномиальный в случае фиксированной размерности пространства.
Доказана NP-полнота задачи о существовании во множестве векторов евклидова пространства такого подмножества векторов неизвестной мощности, что среднее значение квадрата длины их суммы не меньше заданного положительного числа. Для оптимизационного варианта этой задачи обоснован приближённый асимптотически точный алгоритм, полиномиальный в случае фиксированной размерности пространства. К этому варианту задачи сводится поиск во множестве векторов евклидова пространства подмножества векторов "похожих" между собой по критерию минимума суммы квадратов уклонений (в случае, когда мощность искомого подмножества неизвестна). Гипотеза об NP-трудности задачи была неподтвержденной около 10 лет. Задачу можно трактовать как специальный случай задачи кластерного анализа. Полученный результат имеет ключевое значение для анализа комбинаторной сложности и решения математических проблем помехоустойчивого анализа данных и распознавания образов, возникающих, в частности, в электронной разведке, дистанционном зондировании, медицинской и технической диагностике, геофизике, при обработке данных численных экспериментов, тестировании случайных последовательностей на наличие "похожих" участков и др.
Кельманов А. В., Пяткин А. В. О сложности одного из вариантов задачи выбора подмножества "похожих" векторов // Доклады РАН. 2008. Т. 421. № 5. С. 590-592.
Кельманов А. В., Пяткин А. В. Об одном варианте задачи выбора подмножества векторов // Дискретный анализ и исследование операций. 2008. Т.15. № 5. С. 20-34.
Кельманов А. В. Проблема off-line обнаружения повторяющегося фрагмента в числовой последовательности // Труды ИММ Уро РАН. 2008, Т.14. № 2. С. 81-88.
Кельманов А. В., Пяткин А. В. Об одном варианте задачи выбора подмножества векторов // Труды XIV Байкальской международной школы-семинара "Методы оптимизации и их приложения". Иркутск, Байкал, 2-8 июля 2008 г. Т. 1 (Математическое программирование): Иркутск, ИСЭМ СО РАН, 2008. - С. 413-420.
Kel'manov A. V. Discrete Optimization Problem in a Connection With the Off-line Noiseproof Detection of a Repeating Frag-ment in a Numerical Sequence // 9-th Intern. Conf. "Pattern Recognition and Image Analysis: New Information Technologies": Conference Proceedings. Nizhni Novgorod, 2008. Vol. 1. p. 273-275.
Кельманов А. В., Пяткин А. В. О сложности одного из вариантов задачи выбора подмножества "похожих" векторов // Тез. докл. 15-й международной конф. "Проблемы теоретической кибернетики" (Казань, 2-7 июня 2008). Под ред. Ю. И. Журавлева.- Казань: Отечество, 2008.- С. 46.
Кельманов А. В. О некоторых задачах off-line обнаружения повторяющегося фрагмента в числовой последовательности // Тез. докл. междунар. конф. "Алгоритмический анализ неустойчивых задач", посвященной 100-летию со дня рождения В. К. Иванова, 1-6 сентября 2008 г.- Екатеринбург: изд-во Уральского университета, 2008. С. 278-279.
Kel'manov A. V., Pyatkin A. V. On one variant of MSSC problem // Abstracts of International Conference of Operation Re-search. September 3rd - 5th, 2008, University of Augsburg, p. 200.
27. Проведен анализ сверхточных данных о рождении лёгких скалярных мезонов в
фотон-фотонных столкновениях, недавно полученных на b-фабрике в Японии. Выявлены новые указания на
четырёхкварковую природу лёгких скалярных мезонов.
Адронные скалярные каналы в области низких энергий стали камнем преткновения Квантовой Хромодинамики, т.к. ни теория возмущений, ни правила сумм здесь не применимы. В то же время вопрос о природе лёгких скалярных мезонов является главным для понимания механизма реализации киральной симметрии, возникающей в результате пленения кварков.
Более 25 лет назад в лаборатории теоретической физики Института математики было показано, что фотон-фотонные столкновения являются эффективным инструментом поиска четырёхкварковых состояний и предсказано подавление интенсивности рождения четырёхкварковых лёгких скалярных мезонов по сравнению с известными тензорными двухкварковыми мезонами. Недавно в экспериментальных исследованиях произошёл качественный скачок, подтвердивший теоретические ожидания.
В работе представлен анализ механизмов рождения лёгких скалярных мезонов в фотон-фотонных столкновениях на основе новых данных.
Achasov N. N., Shestakov G. N., Phys. Rev. D 77, 074020 (2008).
Ачасов Н. Н., Шестаков Г. Н., Письма в ЖЭТФ, 88, 345 (2008).
|




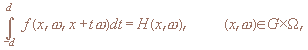
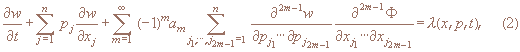
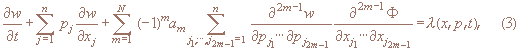
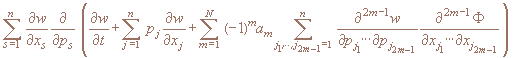
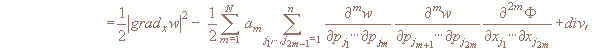
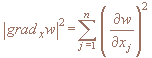
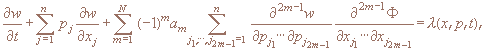
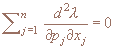 и квадратичные формы
и квадратичные формы