Важнейшие научные результаты Института математики за 2006 год

1. Найдены необходимые и достаточные условия того, что элемент конечного алгебраического расширения нормированного поля порождает целое замыкание кольца нормирования в этом расширении.

Найдены необходимые и достаточные условия того, что элемент конечного алгебраического расширения нормированного поля порождает целое замыкание кольца нормирования в этом расширении. Для такого элемента по его минимальному многочлену конструктивно описывается характер ветвления этого кольца нормирования в данном расширении поля. В случае рациональных чисел результат был получен Р. Дедекиндом в 1878 году.

Ю. Л. Ершов. Критерий Дедекинда для произвольных колец нормирования, ДАН, 410, N 2, 2006, 158-160.

2. Решены проблемы о связи определимости и алгоритмической сложности гиперарифметических свойств в вычислимых графах, частичных порядках и моделях нетривиальной сигнатуры, а также их приложения к некоторым классам классических алгебраических структур.

Изучение алгоритмической сложности определимых отношений, сложности изоморфизмов вычислимых структур, относительно вычислимых структур для тьюринговых степеней лежат в русле современных исследований в теории вычислимых моделей. Ранее в работе С. С. Гончарова, Дж. Найт, В. Харизановой, Р. Соломон, Р. Миллера на основе методов вычислимых нумераций были построены специальные модели, в которые позволили построить специальные модели сигнатуры с несколькими предикатами для решения проблем определимости отношений формулами заданной сложности, существования семейств Скотта заданной сложности и алгоритмической размерности для непредельных уровней арифметической иерархии. Однако оставались нерешенными вопросы существования таких структур в ряде естественных классов вычислимых структур. Основываясь на ранее предложенном С. С. Гончаровым методе сведения категорий вычислимых моделей к категориям графов и частичных порядков, удалось получить сведение построенных ранее моделей к моделям частичных порядков и графов с сохранением заданных алгоритмических свойств. Это позволило докторанту Д. Тусупову распространить полученные результаты на ряд естественных классов алгебраических вычислимых структур.

S. S. Goncharov. Computability and computable models, in Mathematical problems from applied logic II (New logic for the XXI-st Century) Ed.: D. M. Gabbay, S. S. Goncharov, M. Zakharyashev, Springer, NewYork-Boston-Dordrecht-London-Moscow, 2006, pp 99-214.
S. S. Goncharov. Isomorphisms and Definable Relations on Computable Models. Proceedings of Logic Colloguium'2005, Athens, 2006, 22 pp.
Goncharov S.; Harizanov V.; Knight J.; McCoy Ch.; Miller R.; Solomon R. Enumerations in computable structure theory. Ann. Pure Appl. Logic 136 (2005), no.3, 219-246.

3. Решена известная проблема описания монотонного базиса фундированной семантики логических программ.

Решена давно стоящая проблема описания монотонного базиса фундированной семантики логических программ (WFS). Важным преимуществом WFS, предложенной в 1980 году Ван Гелдером и Россом, по сравнению с другими подходами к семантике логических программ с отрицанием является то, что фундированная модель программы всегда существует и единственна. Монотонный базис WFS - это монотонная логика такая, что фундированные модели выделяются как модели данной логики, минимальные относительно предпорядка, не зависящего от конкретной программы. Впервые монотонный базис WFS полностью аксиоматизирован. Определен немонотонный формализм, называемый частичная равновесная логика (PEL) и доказано, что WFS-модели это в точности минимальные PEL-модели. Кроме того, доказано, что пропозициональные теории сильно эквивалентны относительно WFS, если и только если они эквивалентны в монотонным базисе. Формализм частичной равновесной логики расширен на класс дизъюнктных логических программ, проведено его сравнение с другими формализмами, используемыми для работы с дизъюнктными программами. Решена проблема сложности для PEL. Предложено несколько вариантов расширения частичной равновесной логики (PEL) с помощью сильного отрицания. Доказано, что все предложенные формализмы полиномиально эквивалентны PEL. Доказано, что известный вариант фундированной семантики с сильным отрицанием WFSX транслируется в PEL c паранепротиворечивым сильным отрицанием и без принципа когерентности.

Cabalar P., Odintsov S., Pearce D. Logical foundations of well-founded semantics // in: P.Doherty et al. (eds.), Principles of Knowledge Representation and Reasoning: Proceedings of the 10-th International Conference (KR2006), AAAI Press, Menlo Park, California, 2006, pp.25-36.
Cabalar P., Odintsov S., Pearce D., Valverde A. On the logic and computation of partial equilibrium models // in: M.Fisher et al. (Eds.) Proceedings of JELIA'2006 (Lecture Notes in Artificial Intelligence, 4160), Springer, Berlin, 2006, pp.82-94.
Cabalar P., Odintsov S., Pearce D. Strong negation in well-founded and partial stable semantics for logic programs // in: J.S.Sichman et al. (Eds) Proccedings of IBERAMIA-SBIA'2006 (Lecture Notes in Artificial Intelligence, 4140), Springer, Berlin, 2006, pp.592-601.
Cabalar P., Odintsov S., Pearce D., Valverde A. Analysing and extending well-founded and partial stable semantics using partial equilibrium logic // in: S.Etalle and M.Truszczynski (Eds.) Proceedings of ICLP 2006 (Lecture Notes in Computer Science, 4079), Springer, Berlin, 2006, pp.346-360.

4. Для полугруппы элементарных типов булевых алгебр с выделенными идеалами (I-алгебр) доказано, что каждое из свойств I-алгебр: конечная аксиоматизируемость, локальность, счетная категоричность выражается одной формулой первого порядка в полугруппе элементарных типов I-алгебр. Полугруппа является упорядоченной, изучено строение частичного порядка на данной полугруппе.

Изучаются теоретико-модельные свойства булевых алгебр, обогащенных набором одноместных предикатов, выделяющих идеалы (I-алгебр). Исследование теоретико-модельных и алгоритмических свойств булевых алгебр и их обогащений представлено в работах многих авторов – А. Тарского, Ю. Л. Ершова, С. С. Гончарова, М. Рабина, А. Макинтайра, А. С. Морозова, А. Турая и многих других.
При исследовании теоретико-модельных свойств булевых алгебр с выделенными идеалами стало понятным, что многие свойства I-алгебр определяются строением множества прямых слагаемых I-алгебры. В связи с этим возник вопрос об изучении полугруппы элементарных типов булевых алгебр с выделенными идеалами.
Полугруппа E элементарных типов I-алгебр определяется следующим образом: в качестве основного множества берется множество классов элементарной эквивалентности I-алгебр, ее операция – прямое произведение, определенное на классах эквивалентности покомпонентно. Вводится отношение ≤: a ≤ b, если b = a × c для некоторого c E. Показано, что E является коммутативной полугруппой с единицей, а отношение ≤ является частичным порядком на E. Более того, < E; ≤> является упорядоченной полугруппой.
Подполугруппа локальных элементов является начальным сегментом E. Доказано, что под каждым нелокальным элементом E лежит минимальный нелокальный, каждый минимальный нелокальный элемент E является неисчезающим, всего таких элементов континуум.
Доказано, что каждое из свойств I-алгебр: быть неисчезающей, локальной, конечно аксиоматизируемой или счетно категоричной выражается одной формулой первого порядка в полугруппе E элементарных типов I-алгебр. А именно, существуют формулы N(x), L(x), F(x) и C(x) сигнатуры {·} такие что для произвольной I-алгебры A выполнено: A является неисчезающей тогда и только тогда, когда E |= N ([A]_Ξ);
A является локальной тогда и только тогда, когда E |= L([A]_Ξ);
A является конечно аксиоматизируемой тогда и только тогда, когда E |= F([A]_Ξ);
A является w-категоричной тогда и только тогда, когда E |= C([A]_Ξ).
Этот факт особенно интересен потому, что, как показано в данной работе, классы локальных, конечно аксиоматизируемых и w-категоричных I-алгебр не являются аксиоматизируемыми. Таким образом, теоретико-модельные свойства I-алгебр, которые невозможно выразить даже бесконечным множеством формул в исходной, достаточно богатой сигнатуре, выражаются одной формулой сигнатуры {·} в полугруппе элементарных типов.

Pal'chunov D.E. Elementary Type Semigroup for Boolean Algebras with Distinguished Ideals. Mathematical Logic in Asia. Proceedings of the 9th Asian Logic Conference, 2006, p. 175-190.

5. Получена оценка алгоритмической сложности представлений дистрибутивных полурешёток.

В 1972 году Лахланом было получено описание типов изоморфизма главных идеалов полурешётки вычислимо перечислимых m-степеней. Было доказано, что верхняя полурешетка изоморфна главному идеалу в вычилимо перечислимых m-степенях тогда и только тогда, когда она является прямым пределом последовательности конечных дистрибутивных решёток, которую можно задать в виде вычислимой последовательности конечных предпорядков, удовлетворяющей списку из определенных шести свойств. Сейчас такие полурешётки принято называть лахлановскими. Легко установить, что каждая лахлановская полурешётка является ограниченной дистрибутивной верхней полурешёткой с ∑₃⁰-представлением. Автор результата доказывает, что обратное также справедливо и, более того, лахлановское представление ограниченной дистрибутивной полурешётки может быть найдено по её ∑₃⁰ -представлению при помощи эффективной процедуры. Также доказано, что это становится неверным, если понимать  ∑₃⁰ -представления как представления частичных порядков. Это утверждение получено как следствие из двух других доказанных результатов, имеющих самостоятельную ценность. Первый из них заключается в построении примера ограниченной дистрибутивной решётки, которая конструктивизируема как частичный порядок, но не конструктивизируема как верхняя полурешётка. Второй формулируется так: каждый локально решёточный частичный порядок, имеющий 0'-вычислимое представление, имеет  ∑₃⁰ -представление.

Подзоров С. Ю., Об определении лахлановской полурешетки, Сиб. Мат. Ж., 47, N 2, 383 - 393, 2006.

6. Для гомоморфных образов свободного произведения n групп с дополнительными m соотношениями, где n>m, доказано, что если множество связных подгрупп порождает всю группу, то это множество содержит не менее n-m элементов, и в нем найдутся такие n-m подгрупп, которые порождают собственное свободное произведение.

Рассматривается свободное произведение n групп A_i с дополнительными m соотношениями, где n>m, и его фактор-группа G по пересечению подгрупп специального фильтра. Специальный фильтр, например, образуют все нормальные подгруппы, факторы по которым являются разрешимыми группами без кручения. Вводится понятие связной (linked) группы. Класс связных групп достаточно широк, он включает группы без свободных неабелевых подгрупп, любые 2-порожденные несвободные группы, группы, содержащие нетривиальные субнормальные подгруппы с тождеством. Доказывается, что если для каждого i либо образ A_i в G нетривиален, либо абелизация A_i не является периодической группой, и связные подгруппы B₁, …, B_s из G порождают всю группу, то s не меньше n-m и некоторые n-m подгрупп B_j порождают собственное свободное произведение.

N. S. Romanovskiy and John S. Wilson, Free product decompositions in images of certain free products of groups, Journal of Algebra, 2006.

7. Доказано, что из существования нормальной подгруппы конечного индекса, удовлетворяющей полилинейному коммутарному тождеству, вытекает существование характеристической подгруппы ограниченного индекса, удовлетворяющей тому же тождеству. В качестве приложения решена проблема Шумяцкого о почти регулярном автоморфизме порядка 4.

Доказано, что если группа содержит подгруппу конечного индекса, удовлетворяющую полилинейному коммутаторному тождеству, то она содержит характеристическую подгруппу ограниченного индекса, удовлетворяющую тому же тождеству. Ранее подобный результат был известен только для тождества коммутативности. Наличие характеристической подгруппы является важным инструментом во многих случаях, когда идет индукция по длине субнормального ряда. В качестве применения получено следствие о почти регулярном автоморфизме порядка 4 локально конечной группы: из конечности подгруппы неподвижных точек вытекает наличие разрешимой подгруппы конечного индекса (которая, более того, является расширением нильпотентной группы с помощью двуступенно нильпотеной); при этом функция, ограничивающая индекс, и ступень нильпотентности имеют явные оценки.

Макаренко Н. Ю., Хухро Е. И. Большие характеристические подгруппы, удовлетворяющие полилинейному коммутарному тождеству // ДАН, 2006, Т. 411, N 1, С. 16-19.
Макаренко Н. Ю., Хухро Е. И. Почти регулярный автоморфизм порядка 4 // Алгебра и логика, 2006, Т. 45, N 5, С. 575-602.

8. Доказано, что простые группы L_n(2) матриц произвольной размерности n над полем порядка 2 распознаются по множеству порядков элементов.

Многие простые конечные группы однозначно определяются своим набором порядков элементов (т. е. спектром). Однако проблема описания всех таких групп ещё далека от полного решения. Для классических групп важным шагом является изучение спектра их собственных накрытий и, как следствие, неприводимых модулярных представлений. Одним из результатов является решение проблемы распознаваемости для бесконечной серии групп PSL(n,2) – группы всех матриц произвольной размерности над полем порядка 2.

Заварницин А. В., Мазуров В. Д. Порядки элементов в накрытиях конечных простых линейных и унитарных групп и распознаваемость групп L(n,2) по спектру // Доклады Академии Наук, 2006, Т 409, N 6, 736-739.

9. Решена проблема Татта (1963) оnbsp;подсчёте неизоморфных карт на компактной римановой поверхности.

Разработан общий метод для нахождения числа карт и гиперкарт на римановых поверхностях и орбифолдах. Найдена точная формула для числа гиперкарт на замкнутой римановой поверхности с точностью до произвольного гомеоморфизма.

Mednykh A., Nedela R. Enumeration of unrooted maps with given genus // Journal of Combinatorial Theory. Ser(B). 2006. V. 96, P. 706-729.

10. Доказана теорема об однозначной определенности конформного типа выпуклых многогранников.

Предложен новый подход к классической проблеме однозначной определенности замкнутых выпуклых поверхностей, существенно расширяющий ее рамки. Доказана теорема об однозначной определенности выпуклых многогранных областей относительными конформными модулями граничных конденсаторов.

Копылов А. П. Однозначная определенность выпуклых многогранных областей относительными конформными модулями граничных конденсаторов // Докл. АН. 2006. Т. 410, N 1. С. 21-23.

11. Найдены необходимые и достаточные условия на образ и прообраз липшицева отображения, определенного на измеримом множестве в Rⁿ и принимающего значения в произвольном метрическом пространстве, для справедливости формулы коплощади. Получен метрический аналог теоремы о неявной функции.

Исследованы липшицевы отображения, определенные на Hⁿ-прямляемом метрическом пространстве со значениями в произвольном метрическом пространстве. Найдены необходимые и достаточные условия на образ и прообраз отображения для справедливости формулы коплощади. В частности, показано, что H^k-прямляемость образа - не только достаточное, но также и необходимое условие. Кроме этого, получено еще 3 эквивалентных утверждения. В качестве следствия, установлена формула коплощади для отображений, принимающих значения в произвольном метрическом пространстве, образ которых H^k-сигма-конечен. Все эти результаты являются новыми и в случае отображения двух евклидовых пространств произвольных размерностей. Установлен "метрический" аналог теоремы о неявной функции. Все вышеперечисленные результаты распространены на широкие классы отображений, в частности, на отображения классов Соболева и BV-отображения со значениями в метрическом пространстве.

Карманова М. Б. Спрямляемые множества и формула коплощади для отображений со значениями в метрическом пространстве // Докл. АН. 2006. Т. 408, N 1, С. 16-21.
Karmanova M. Geometric Measure Theory Formulas for Metric-Valued Mappings // Contemporary Mathematics, T. 424. In: "The Interaction of Analysis and Geometry" (2007), P. 103-137.

12. Получены описания следов классов дифференцируемых функций (включая пространства Соболева) на множествах групп Карно.

Доказаны классические теоремы типа Уитни о следах и продолжении для гладких функций на группах Карно. Получена обратимая характеристика следов функций из пространств Соболева W_∞^I и Никольского H_∞^I, заданных в произвольной области группы Карно. Получена обратимая характеристика следов функций из пространств Соболева W_p^I, заданных на группе Карно, на замкнутых множествах, удовлетворяющих некоторым условиям регулярности, называемых множествами Альфорса. Доказана теорема о продолжении за границу области функций классов Соболева W_p^I, заданных в (ε,δ)-области на двухступенчатой группе Карно. В качестве следствия получена обратимая характеристика следов функций из пространств Соболева W_p^I, заданных в ограниченной области класса C² на двухступенчатой группе Карно. В качестве приложения теорем о следах получена теорема существования и единственности слабого решения краевой задачи для полисубгармонического уравнения в ограниченной области класса C² на двухступенчатой группе Карно.

Водопьянов С. К., Пупышев И. М. Теоремы типа Уитни о продолжении функций на группе Карно // Докл. АН, 2006. T. 406, N 5. С. 586-590.
Водопьянов С. К., Пупышев И. М. Теоремы типа Уитни о продолжении функций на группе Карно // Сиб. мат. журн., 2006. T. 47, N 4.
Водопьянов С. К., Пупышев И. М. О граничных значениях дифференцируемых функций, заданных в произвольной области группы Карно // Докл. АН. 2006. T. 408, N 3. С. 295-300.
Водопьянов С. К., Пупышев И. М. О граничных значениях дифференцируемых функций, заданных в произвольной области группы Карно // Математические труды, 2006. T. 9, N 2. С. 23-46.
Водопьянов С. К., Пупышев И. М. Следы пространств Соболева на множествах Альфорса групп Карно // Докл. АН, 2006. Т. 411, N 2.

13. Найдены необходимые и достаточные условия на нигде не плотное множество, чтобы оно было множеством значений градиента C¹-гладкой функции двух переменных.

Изучены свойства C¹-гладких функций v двух переменных, у которых внутренность множества значений градиента пуста. Доказано, что в этом случае множество значений градиента функции v локально представляет собой кривую, которая имеет касательные в некотором слабом смысле, и направление этих слабых касательных меняется как функция ограниченной вариации. Основным инструментом является некоторый аналог теоремы Сарда для C¹-гладких функций двух переменных.

Коробков М. В. Свойства C¹-гладких функций, образ градиента которых является нигде не плотным множеством // Докл. АН. 2006. Т. 410, N 5. С. 596–598.
Коробков М. В. Об одном аналоге теоремы Сарда для C¹-гладких функций двух переменных // Сиб. мат. журн. 2006. Т. 47, N 5, С. 1083-1091.

14. Получены условия компактности вложения следов соболевских функций в пространства Лебега на границе “нулевых” пиков с гёльдеровыми особенностями в вершине.

Метод доказательств основан на использовании результатов теории обобщенных классов соболевского типа на метрических пространствах. На метрическом пространстве с борелевской мерой, удовлетворяющей “условию удвоения” , для введенных ранее П. Хайлашем пространств соболевского типа HW_p^I, получены общие теоремы о компактности вложения следов в пространства Лебега на множествах меньшей “размерности”. Для “нулевых” пиков G_λ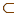Rⁿ  с гельдеровыми особенностями в вершине установлена взаимосвязь между классическими пространствами Соболева W_p^I(G_λ) и пространствами соболевского типа HW_p^I(G_λ). Использование этой взаимосвязи и результатов для пространств соболевского типа HW_p^I позволяет получить точные оценки на показатель суммируемости q, при которых на границе “нулевого” пика вложение следов функций из пространств Соболева W_p^I(G_λ) в пространства Лебега L_p(∂G_λ) будет компактным.

Романов А. С. О следах соболевских функций на границе пика с гельдеровой особенностью // Сиб. мат. журн. (сдана в ноябре 2005, принята в печать), 9 стр.
Романов А. С. О следах функций, принадлежащих обобщенным классам соболевского типа // Сиб. мат. журн. (сдана в марте 2006, принята в печать), 15 стр.

15. Получены оценки устойчивости решений краевых задач для уравнений нестационарной упругости при заданных на границе физической области смещениях и напряжениях. Подобные оценки найдены также для уравнений электродинамики с заданными на границе тангенциальными компонентами электромагнитного поля.

Для динамической системы уравнений упругости, отвечающей неоднородной изотропной упругой среде, рассмотрена краевая задача о построении решения этой системы, когда на границе компактной физической области задаются смещения точек среды и напряжения на площадках, нормальных к границе. Предполагается, что эти смещения и напряжения задаются на конечном отрезке времени. Задание начальных условий не предполагается. Получены оценки устойчивости решений рассматриваемой задачи и не улучшаемая оценка снизу длины временного интервала, при котором полученная оценка устойчивости справедлива. Оценки устойчивости решений получены для системы уравнений электродинамики при заданных на границе компонентах электромагнитного поля и заданном начальном распределении зарядов. В зависимости от длины временного интервала, эти оценки являются гельдеровыми или липшициевыми.

Результаты опубликованы в статьях:
ДАН, 2006, т, 410, N 2, с. 161-163,
ДАН, 2006, т, 411, N 1, с. 25-27.
Докладывались на международной конференции «Тихонов и современная математика», Москва, 19-25 июня 2006 г..

16. Доказаны теоремы об изоморфизме для класса матричных квазиэллиптических операторов в специальных весовых соболевских пространствах. Показана разрешимость краевых задач для квазиэллиптических систем.

Изучены свойства класса матричных квазиэллиптических операторов в Rⁿ. Предполагается, что символы этих операторов квазиоднородны. Примерами таких операторов являются: эллиптические операторы по Петровскому, эллиптические операторы по Дуглису-Ниренбергу (в частности, стационарный оператор Навье-Стокса), параболические операторы, параболические операторы «с противоположными временами» и др. Для рассматриваемого класса операторов установлены теоремы об изоморфизме в специальных весовых соболевских пространствах. Такие пространства были введены автором, и в частных случаях они совпадают с известными пространствами Кудрявцева и пространствами Ниренберга-Уолкера-Кантора. Доказанные теоремы об изоморфизме обобщают известные результаты для однородных эллиптических операторов (R. C. McOwen, R. B. Lockhart, Y. Choquet-Bruhat, D. Christodoulou) и для однородных квазиэллиптических операторов
(Г. В. Демиденко, G. N. Hile). Полученные результаты используются при доказательстве разрешимости краевых задач в R₊ⁿ для квазиэллиптических систем.

Демиденко Г. В. Об одном классе матричных дифференциальных операторов // СМЖ. 2004. Т. 45, N 1. С. 103-118.
Demidenko G. V. On solvability of boundary value problems for quasi-elliptic systems in R₊ⁿ // J. Anal. Appl. 2006. V. 4, N 1. P. 1-11.
Demidenko G. V. On properties of matrix quasielliptic operators // Int. J. Dyn. Syst. Diff. Eq. (принята к печати).

17. Создана теория интегрирования неслучайных функций по произвольному неортогональному гильбертову шуму. Приведены простые достаточные условия существования таких интегралов для широких классов интегрирующих случайных процессов, в частности, гауссовских. С помощью этих интегралов описаны предельные распределения для статистик Мизеса и U-статистик, построенных по слабо зависимым наблюдениям.

Так называемые статистики Мизеса и U-статистики (специальные функции от наблюдаемых величин) широко применяются при построении статистических критериев для принятия тех или иных решений по результатам многократных наблюдений (или испытаний) некоторых зашумленных характеристик, точное знание которых исключено в силу объективных причин. До настоящего времени была хорошо разработана теория построения таких критериев с использованием упомянутых выше статистик только в случае, когда результаты наблюдений независимы, т.е. никак не связаны друг с другом. Подобная схема реализуется далеко не всегда. Не менее популярна модель наблюдения стационарного случайного процесса, у которого близкие по времени испытания могут быть существенно зависимыми. Простым примером может служить ежедневно наблюдаемая температура воздуха в течение одного, скажем, зимнего или летнего месяца. Упомянутые критерии основаны на знании распределений значений статистик как функций от наблюдений в зависимости от тех или иных предположений исследователя относительно наблюдаемого случайного процесса. Вычисление точных распределений, как правило, возможно только в исключительных случаях. На практике при больших объемах наблюдений вместо точных используются приближенные оценки таких распределений. Обоснование подобной замены дается так называемыми предельными теоремами математической статистики. Работа И. С. Борисова и А. А. Быстрова как раз и посвящена распространению известных предельных теорем для упомянутых выше статистик на случай стационарно связанных наблюдений. Для этого, в частности, потребовалось построить аналог кратного стохастического интеграла Винера - Ито в случае, когда интегрирующий случайный процесс имеет неортогональные (т.е. зависимые) приращения. Как оказалось, именно такие интегралы и описывают предельные распределения упомянутых статистик Мизеса и U-статистик.

Теория вероятн. и ее примен., 2005, т. 50, N 1, c. 52-80.
Сибирский матем. журнал, 2006, т. 47, N 6, 1205-1217.

18. Получены интегро-локальные и интегральные теоремы, действующие на всей оси, для сумм случайных величин с семиэкспоненциальными распределениями.

Для сумм случайных величин с семиэкспоненциальными распределениями (т.е. с распределениями, убывающими на бесконечности быстрее, чем степенным образом, и медленнее, чем экспоненциальным) получены интегро-локальные и локальные предельные теоремы, действующие на всей оси, т.е. описывающие вероятности больших уклонений во всех зонах уклонений, включая граничные (промежуточные) области. Исследуемая асимптотика в граничных зонах долгое время оставалась неизвестной.

Сибирский матем. журнал, 2006, т. 47, N 6, 1218-1257.

19. Получены оценки скорости сильной сходимости градиентных методов решения сильно некорректных задач (задача Коши для уравнения Лапласа, задача Коши для параболического уравнения с обратным временем и др.). На основе этих оценок, получено новое правило нахождения конечного номера итерации в градиентных методах.

Рассмотрены два из важнейших направлений развития теории обратных и некорректных задач:
1) оценки условной устойчивости решения,
2) оценки скорости сходимости градиентных методов.
Первое из указанных направлений является преимущественно теоретическим, поскольку имеет условный характер, а именно, уклонение решения некорректной задачи Aq=f от решения той же задачи, но с приближенными данными, удается оценить лишь в том случае, когда решение задачи с приближенными данными существует и принадлежит заданному множеству (множеству корректности). Проверить такое условие на практике редко удается.
Второе направление, наоборот, привлекает пристальное внимание практиков, поскольку только оценка скорости сходимости (даже условная) позволяет (при отсутствии теоремы существования решения некорректной задачи) согласовывать уровень погрешности данных f некорректной задачи с выбором параметра регуляризации, роль которого в итерационных (и в частности, в градиентных) методах играет номер итерации.
Долгое время два указанных направления развивались параллельно и независимо. Особенно интенсивно разрабатывались градиентные методы, основанные на минимизации соответствующего целевого функционала J(q)=<Aq-f,Aq-f>, поскольку их реализация сводится к последовательному решению ряда соответствующих корректных задач (прямой и сопряженной). Это позволяет использовать весь арсенал численного решения (прямых) задач математической физики.
Полученные результаты позволяют связать скорость сходимости ряда известных алгоритмов решения некорректных задач (методы наискорейшего спуска, сопряженных градиентов, итерации Ландвебера и другие) с весьма тонкими математическими свойствами исследуемой задачи – с оценками условной устойчивости решения. Найденные оценки приводят к точным алгоритмам выбора номера итерации, являющимся в случае некорректной задачи параметром регуляризации, по заданному уровню погрешности данных. В частности, удалось получить новое правило нахождения номера итерации, на котором следует остановить решение некорректной задачи. Ранее наиболее известным правилом остановки процесса был принцип невязки (иногда называемый принципом Морозова), в соответствии с которым процесс останавливался в том случае, если невязка ||Aq-f||, которая в общем случае монотонно убывает, оказывалась меньше уровня погрешности данных (или в некотором смысле сравнима). В 2006 году было показано, что если для некорректной задачи получена оценка условной устойчивости, то, используя эту оценку, можно найти номер остановки, который позволяет получить заданную точность решения за меньшее количество итераций, чем требует принцип невязки.

Kabanikhin S. I. Estimation of the convergence rate of gradient methods of solving inverse and ill-posed problems via conditional stability estimates. // Journal of Inverse and Ill-Posed Problems, 2005, 13(3), 259-264.
Kabanikhin S. I. Conditional stability stopping rule for gradient methods applied to inverse and ill-posed problems. // Journal of Inverse and Ill-Posed Problems, 2006, 14(8), 805-812.

20. Предложен новый подход к построению интерполяционных сплайнов высоких степеней. Найдена связь обусловленности получаемых систем уравнений со сходимостью процессов интерполяции. Установлена симметрия условий сходимости процессов интерполяции для младших и старших производных, в частности, выделены хорошо обусловленные методы построения, и положительно решена гипотеза К. де Бора (1975) о безусловной сходимости ещё одной средней производной сплайнов.

В работе предложен новый подход к получению систем определяющих уравнений для построения интерполяционных сплайнов произвольной нечётной степени, состоящий в вычислении сплайна через коэффициенты разложения по нормализованным B-сплайнам какой-либо его производной. Изучены свойства возникающих систем уравнений, указаны способы эффективного вычисления их элементов. Выделены устойчивые хорошо обусловленные системы. Ранее надёжные методы построения интерполяционных сплайнов были известны только для сплайнов невысоких степеней. Новый подход даже в хорошо изученном случае кубических сплайнов привёл к новому устойчивому способу построения интерполяционных кубических сплайнов.
Доказано, что вопрос о хорошей обусловленности возникающей здесь системы уравнений, например для k-й производной, эквивалентен вопросу об ограниченности нормы оператора P^(k), сопоставляющего k-й производной интерполируемой функции соответствующую производную интерполяционного сплайна или вопросу сходимости процесса интерполяции k-й производной для любой интерполируемой функции с непрерывной k-й производной. Установлено, что для сплайна степени 2n-1 системы уравнений, соответствующие производным k и 2n-1-k, имеют эквивалентную обусловленность. Это означает, что если величина обусловленности одной из указанных систем может быть ограничена константой, не зависящей от неравномерности сетки, то величина и другой системы также может быть ограничена аналогичной константой.
В 1975 году К. де Бор высказал предположение, что только нормы операторов P^(n-1) и P⁽ⁿ⁾ ограничены при любом расположении узлов сетки. В 2001 году А. Шадрин доказал это предположение для P⁽ⁿ⁾. Установленная симметрия условий сходимости процессов интерполяции для младших и старших производных позволила получить решение гипотезы К. де Бора о безусловной сходимости остававшейся ещё одной средней производной сплайнов при минимальных требованиях гладкости интерполируемой функции.

Volkov Yu. S. Totally positive matrices in the methods for constructing interpolation splines of odd degree // Siberian Adv. in Math. – 2005. – V. 15, n. 4. – P. 96-125.
Волков Ю. С. Безусловная сходимость ещё одной средней производной для интерполяционных сплайнов нечётной степени // ДАН. – 2005. - Т. 401, N 5. – С. 592-594.
Волков Ю. С. Условия ограниченности операторов сплайн-интерполяции. – Новосибирск, 2006. – 18 с. – (Препринт N 167 / РАН. Сиб. отд-ние. Ин-т математики им. С. Л. Соболева).

21. Построено описание процесса рождения пары векторных мезонов в квантовой хромодинамике - современной теории сильных взаимодействий. Впервые для физического процесса удалось получить выражение для амплитуды с учетом следующих за ведущими логарифмов энергии, что позволило получить устойчивые предсказания для амплитуды и ее зависимости от энергии.

Построено описание процесса рождения пары векторных мезонов в квантовой хромодинамике – современной теории сильных взаимодействий. При высоких энергиях разложение по константе связи содержит большие вклады, усиленные логарифмами энергии. При этом возникает необходимость суммирования таких вкладов во всех порядках теории возмущений. БФКЛ метод позволяет в общем случае осуществить такое суммирование, как для ведущих, так и для следующих за ведущими логарифмов энергии. При этом амплитуда процесса может быть представлена в виде свертки функции Грина и вершинных функций.
Функция Грина универсальна, не зависит от процесса. Вершинные же функции не универсальны, они должны определяться для каждого процесса отдельно. Учёт первых не ведущих логарифмов является принципиально важным, поскольку он позволяет зафиксировать параметры определяющие масштаб для энергии и масштаб для бегущей константы связи. Эти параметры остаются полностью произвольными при учете только ведущих логарифмических вкладов. Уравнение для функции Грина известно, в настоящее время, с учетом вкладов первых не ведущих логарифмов. Тогда как вершинные функции были известны только с главной логарифмической точностью. В данной работе получены выражения для вершинных функций описывающие переход виртуального фотона в векторный мезон. Впервые для физического процесса построено представление для амплитуды с учетом следующих за ведущими логарифмов энергии. На основе этого получены устойчивые предсказания для амплитуды и ее зависимости от энергии.

D. Yu. Ivanov, A. Papa, “Electroproduction of two light vector mesons in the next-to-leading approximation” Nuclear Physics B 732 (2006) 183-199.

22. Доказаны теоремы существования и кооперативной характеризации информационных равновесий.

Представлены итоговые результаты, касающиеся существования и кооперативной характеризации информационных равновесий, введенных В. Л. Макаровым для моделей обмена с неавтономными предпочтениями (экстерналиями). Модели обмена с экстерналиями являются полезным инструментом анализа различных схем согласования интересов в задачах финансирования благ коллективного пользования (безопасность окружающей среды, фундаментальная наука, образование и т.п.). Однако классические вальрасовские равновесия в этих моделях являются, как правило, неэффективными, что и потребовало разработки иных, альтернативных принципов оптимальности. Информационные равновесия, являясь реализациями одного из таких принципов, помимо Парето-оптимальности обладают целым рядом других важных свойств. Так, согласно одному из главных результатов работы, их существование гарантируется в предположениях, близких к самым общим условиям существования классических вальрасовских равновесий. Далее, информационные равновесия оказываются эффективными в следующей усиленной форме: все они коалиционно стабильны.
Наконец, как установлено в одном из итоговых результатов, для широкого класса моделей с экстерналиями множество информационных равновесий совпадает с представительным нечетким ядром, что открывает новые возможности для применения методов теории кооперативных игр при анализе изучаемого понятия равновесия.

Макаров В. Л., Васильев В. А. Информационное равновесие. Существование // Экономика и математические методы, 2006. Том 42, N 3, с. 31-52.
Макаров В. Л., Васильев В. А. Информационное равновесие. Коалиционная стабильность // Экономика и математические методы, 2006. Том 42, N 4, с. 50-63.

23. Построен приближенный алгоритм кубической трудоёмкости отыскания двух непересекающихся гамильтоновых циклов максимального суммарного веса с оценкой точности 3/4.

Исследована аппроксимируемость задачи о нахождении двух реберно-непересекающихся гамильтоновых циклов максимального веса в полном неориентированном реберно-взвешенном графе, известная в литературе как 2-peripatetic salesman problem. Известно, что данная задача NP-трудна, что делает актуальным вопрос о существовании приближенных алгоритмов с гарантированными оценками точности. Для решения задачи построен полиномиальный алгоритм с константной оценкой точности 3/4 и временной сложностью O(n³), где n - число вершин в графе. Алгоритм начинает работу с построения либо кубического подграфа (при чётном числе вершин), либо "почти кубического" подграфа (при нечётном числе вершин) максимального веса, который затем особым образом подвергается разбиению на два реберно-непересекающихся частичных тура. Найденные частичные туры в дальнейшем с помощью специальной процедуры удается дополнить до непересекающихся по рёбрам гамильтоновых циклов, что не всегда возможно в общем случае. Эти гамильтоновы циклы поступают на выход алгоритма как решение задачи. Оценка точности алгоритма вытекает из того факта, что вес разбиваемого подграфа не меньше 3/4 веса оптимального решения.

Агеев А. А., Бабурин А. Е., Гимади Э. Х. Полиномиальный алгоритм с оценкой точности 3/4 для отыскания двух непересекающихся гамильтоновых циклов максимального веса // Дискретный анализ и исследование операций. Серия 1. Изд-во ИМ СО РАН им. С. Л. Соболева, Новосибирск , 2006. Т. 12, N 2, С. 11-20.

24. Предложено конструктивное описание n-квазигрупп порядка 4.

Каждая n-арная квазигруппа порядка 4 может быть получена посредством по крайней мере одной из конструкций: через суперпозицию квазигрупп меньшей арности или как преобразование линейной n-арной квазигруппы, задаваемое некоторой булевой функцией.
Функция f:{0,…,k-1}ⁿ → {0,…,k-1} называется n-квазигруппой порядка k, если она обратима по каждой переменной. Компонентой будем называть подмножество {0,…,k-1}ⁿ, если сужение f на него является n-квазигруппой меньшего порядка. Область определения линейной n-квазигруппы порядка 4 разделяется на компоненты. n-Квазигруппа порядка 4 называется полулинейной, если она может быть получена из линейной сдвигом компонент, определяемым некоторой булевой функцией. Доказано, что любая неразложимая, т. е. не представимая в виде суперпозиции m-квазигрупп меньшей размерности n-квазигруппа порядка 4 является полулинейной. Получена асимптотика числа n-квазигрупп порядка 4 при n→∞.

Потапов В. Н., Кротов Д. С. Асимптотика числа n-квазигрупп порядка 4 // СМЖ. 2006. Т. 47, N 4. С. 873-887.

25. Разработана новая техника глобального перераспределения эйлеровых вкладов в плоских графах и найдены новые свойства турниров Пэли, что позволило улучшить известные верхние оценки ориентированного хроматического числа плоских графов, имеющих заданный обхват.

Ориентированная k-раскраска орграфа G есть гомоморфизм из G в некоторый k-вершинный турнир H (мишень), т.е. вершины орграфа H считаются цветами, и требуется каждой вершине из G приписать цвет так, чтобы любая дуга в G, начало которой окрашено в цвет i, а конец – в j, имелась бы в мишени H.
Установлен ряд новых свойств турниров Пэли, в частности, P(47), т.е. турнира на вершинах 0,1, …, 46, в котором пара ij является дугой из i в j, если и только если j=(i+q_k) mod 47, где q_k – один из 23 квадратичных вычетов по mod 47. Это позволило доказать ориентированную 47-раскрашиваемость плоских графов без треугольников (ранее была известна верхняя оценка 59).
Доказано, что любой плоский граф обхвата не менее 12 допускает гомоморфизмы на циркулянт C(5;1,2) (этот вопрос был поставлен в 1995 г.). В доказательстве используется идея глобального перераспределения эйлеровых вкладов, не встречавшаяся до сих пор в работах по плоским графам. Ориентированная раскраска тесно связана с антисимметрическими потоками в графах и гипотезой Жеже (1981) о круговых потоках. В свою очередь, гипотеза Жеже является усилением гипотезы Татта о 5-потоках. Дальнейшие усилия исследователей будут направлены на доказательство ориентированной 5-раскрашиваемости плоских графов с обхватом от 11 до 8. В этой работе будет полезна лемма о "мягком" цикле [3], поскольку она верна для графов произвольного обхвата и накладывает существенные ограничения на структуру минимального контрпримера. По-видимому, глобальность перераспределения вкладов, успешно использованная в случае обхвата 12, будет играть важную роль и для меньших обхватов.

Бородин О. В., Иванова А. О. Ориентированная 7-раскраска плоских графов с обхватом не менее 7 // Сибирские Электронные Математические Известия. 2005. Т. 2. С. 222-229.
Бородин О. В., Иванова А. О. Ориентированная раскраска плоских графов с обхватом не менее 4 // Сибирские Электронные Математические Известия. 2005. Т. 2. С. 239-249.
Бородин О. В., Иванова А. О., Косточка А. В. Ориентированная 5-раскраска вершин в разреженных графах // Дискрет. анализ и исслед. операций. Сер. 1. 2006. Т. 1, N 1. С. 16-32.

26. Предложен подход к оптимизации размещения взаимосвязанных объектов с учетом запрещенных зон, основанный на применении целочисленного программирования.

Рассматриваются задачи размещения взаимосвязанных объектов на плоскости при наличии прямоугольных запрещенных зон с минимаксным критерием и критерием минимальной суммарной стоимости связей (задачи Вебера). Предложен подход для решения задач указанного класса на основе построения моделей целочисленного линейного программирования. Указанный подход позволяет применять достаточно разработанный аппарат целочисленной оптимизации (методы ветвей и границ, отсечений, перебора L-классов и др). Для частных случаев предложены полиномиальные комбинаторные алгоритмы.

Забудский Г. Г. Алгоритм решения минимаксной задачи размещения объекта на плоскости с запрещенными зонами// Автоматика и телемеханика. - 2004. - N 4 - С. 93-100.
Забудский Г. Г. О минимаксной и минисуммной задачах размещения на плоскости с запрещенными областями // Труды 13-й Байкальской международной школы-семинара "Методы оптимизации и их приложения", Т. 1. - Иркутск, 2005. - C. 455-460.

27. Изучена сложность и найдены решения ряда новых задач комбинаторной оптимизации, возникающих при реализации апостериорного (off-line) подхода к помехоустойчивому анализу и распознаванию числовых последовательностей, имеющих квазипериодическую структуру; обоснованы точные и приближенные полиномиальные алгоритмы решения этих задач.

Изучена вычислительная сложность и найдены решения ряда новых задач комбинаторной оптимизации, возникающих при реализации апостериорного (off-line) подхода к помехоустойчивому анализу и распознаванию числовых последовательностей, имеющих квазипериодическую структуру (квазипериодическое изменение свойств) [1]. Обоснованы полиномиальные алгоритмы, гарантирующие отыскание оптимального (максимально правдоподобного) решения следующих задач:
1) совместного обнаружения квазипериодических фрагментов из эталонного набора в числовой последовательности и ее разбиения на участки, включающие серии одинаковых фрагментов (случаи известного числа фрагментов) [2];
2) апостериорного обнаружения в числовой последовательности заданного числа ненулевых информационных квазипериодических фрагментов [3];
3) совместного обнаружения и идентификации квазипериодических фрагментов в последовательности по их обрывкам (случаи известного и неизвестного числа фрагментов) [4], [5];
4) распознавания последовательности, включающей серии квазипериодически повторяющихся эталонных фрагментов (случаи известного числа фрагментов) [6];
Доказана NP-трудность задачи обнаружения в числовой последовательности квазипериодического фрагмента при заданном числе повторов; обоснован приближенный алгоритм ее решения [7]. Перечисленные результаты, с одной стороны, пополняют список изученных задач дискретной оптимизации, а с другой, - заполняют существовавший пробел в области математических методов анализа данных и распознавания образов. Полученные результаты применимы в электронной разведке, радиолокации, гидроакустике, геофизике и дистанционном зондировании, технической и медицинской диагностике, криминалистике и эконометрике, обработке речевых сигналов и изображений, телекоммуникации, биометрике и других приложениях, связанных с извлечением информации из потоков зашумленных и несинхронизированных (рассогласованных по времени) данных. Практическая ценность результатов состоит в возможности получения наилучших (оптимальных) решений для целого ряда типовых задач, возникающих в перечисленных приложениях.

Кельманов А. В. Проблемы оптимизации в типовых задачах помехоустойчивой апостериорной обработки числовых последовательностей с квазипериодической структурой // Материалы 3-й Всероссийской конференции "Проблемы оптимизации и экономические приложения". Омск, 2006. С. 37-41. (пленарный доклад)
Кельманов А. В., Михайлова Л. В. Совместное обнаружение в квазипериодической последовательности заданного числа фрагментов из эталонного набора и ее разбиение на участки, включающие серии одинаковых фрагментов // Журнал вычислительной математики и математической физики, 2006, Т. 46, N 1, С. 172-189.
Кельманов А. В., Хамидуллин С. А. Апостериорное обнаружение в числовой последовательности заданного числа неизвестных квазипериодических фрагментов // Сибирский журнал индустриальной математики. 2006. Т. 9 N 3(27). С. 50-65.
Kel'manov A. V., Khamidullin S. A. Simultaneous A Posteriori Detection and Identification of a Predetermined Number of Quasi-periodic Fragments in a Sequence Based on Their Segments // Pattern Recognition and Image Analysis. 2006. Vol. 16, No. 3, pp. 344-357.
Кельманов А. В., Хамидуллин С. А. Совместное апостериорное обнаружение и идентификация квазипериодических фрагментов в последовательности по их обрывкам // Сибирский журнал индустриальной математики. 2006. Т. 9 N 2(26). С. 55-74.
Kel'manov A. V., Mikhailova L. V. Recognition of a Numerical Sequence Containing Series of Quasi-Periodically Repeating Reference Fragments: The Case of a Known Number of Fragments // Pattern Recognition and Image Analysis. 2006. Vol. 16, No. 3, pp. 358-370.
Гимади Э. Х., Кельманов А. В., Кельманова М. А., Хамидуллин С. А. Апостериорное обнаружение в числовой последовательности квазипериодического фрагмента при заданном числе повторов // Сибирский журнал индустриальной математики. 2006. Т. 9 N 1(25). С. 55-74.